- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Средства анализа презентация
Содержание
- 1. Средства анализа
- 2. Лекция 1 Средства анализа Что такое время
- 3. Лекция 1 Средства анализа Рис. 3.1.
- 4. Лекция 1 Средства анализа Недостатки экспериментального исследования
- 5. Лекция 1 Средства анализа Сущность такой методологии
- 6. Лекция 1 Средства анализа Часто программистам удобно
- 7. Лекция 1 Средства анализа 3.2.1. Пример псевдокода
- 8. Лекция 1 Средства анализа public class ArrayMaxProgram
- 9. Лекция 1 Средства анализа Что такое псевдокод
- 10. Лекция 1 Средства анализа 1. Записать алгоритм
- 11. Лекция 1 Средства анализа Удобнее проводить анализ
- 12. Лекция 1 Средства анализа Подсчет числа простейших
- 13. Лекция 1 Средства анализа Анализ средних и
- 14. Лекция 1 Средства анализа Асимптотическая нотация Очевидно,
- 15. Лекция 1 Средства анализа Нотация большого О
- 16. Лекция 1 Средства анализа
Слайд 1Лекция 1 Средства анализа
Структура данных — это систематизированный способ организации данных
Алгоритм — поэтапная процедура выполнения некоего задания за определенный период времени.
Нужно стремиться к «качественным» структурам данных и алгоритмам. Для этого нужны точные приемы их анализа. Две основные характеристики анализа:
1. Затраты времени на выполнение алгоритмов и операций над структурами данных.
2. Размер используемой данными памяти (оперативная память и дисковое пространство).
Слайд 2Лекция 1 Средства анализа
Что такое время выполнения алгоритма?
Время выполнения зависит от
Экспериментальные исследования
Можно регистрировать действительное время в каждом отдельном случае выполнения алгоритма с различными исходными данными. Подобные измерения должны проводиться с достаточной точностью с помощью системных вызовов, встроенных в язык или операционную систему, для которой написан данный алгоритм (например, свойства System.DateTime.Now). Для обобщения потребуется определить, каким образом время выполнения программы зависит от количества исходных данных. Для решения этой задачи можно провести ряд экспериментов, в которых будет использовано различное количество исходных данных.
Необходимо использовать качественные образцы исходных данных и провести достаточно большое число экспериментов.
Далее полученные результаты наглядно представляются с помощью графика, где каждый случай выполнения алгоритма обозначается с помощью точки, координата X которой равна размеру исходных данных n, а координата Y — времени выполнения алгоритма t (см. рис. 1.1).
Слайд 3Лекция 1 Средства анализа
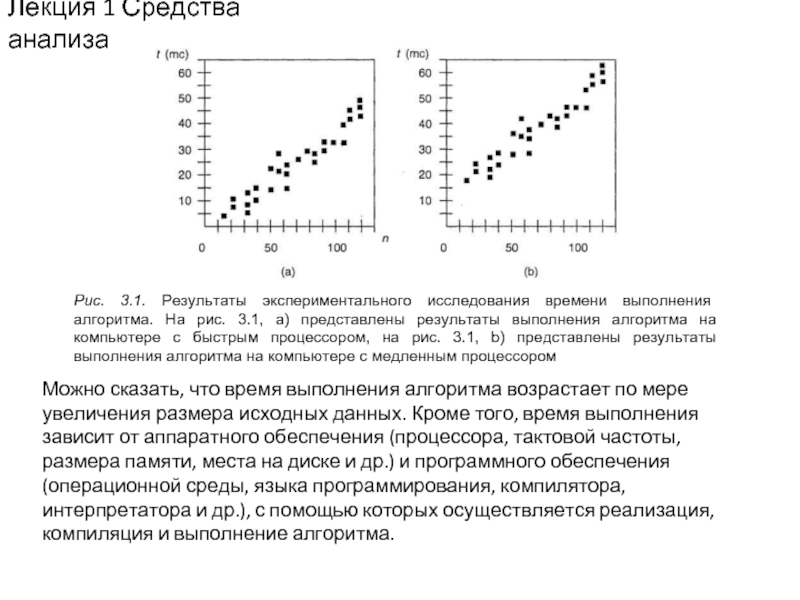
Рис. 3.1. Результаты экспериментального исследования времени выполнения алгоритма.
Можно сказать, что время выполнения алгоритма возрастает по мере увеличения размера исходных данных. Кроме того, время выполнения зависит от аппаратного обеспечения (процессора, тактовой частоты, размера памяти, места на диске и др.) и программного обеспечения (операционной среды, языка программирования, компилятора, интерпретатора и др.), с помощью которых осуществляется реализация, компиляция и выполнение алгоритма.
Слайд 4Лекция 1 Средства анализа
Недостатки экспериментального исследования
- эксперименты могут проводиться лишь с
- для сравнения эффективности двух алгоритмов необходимо, чтобы эксперименты по определению времени их выполнения приводились на одинаковом аппаратном и программном обеспечении;
для экспериментального изучения времени выполнения алгоритма необходимо провести его реализацию и выполнение.
Поэтому более удобная методология анализа времени выполнения алгоритмов, должна:
- учитывать различные типы входных данных;
- позволять производить оценку относительной эффективности любых двух алгоритмов независимо от аппаратного и программного обеспечения;
- проводиться по описанию алгоритма без его непосредственной реализации или экспериментов.
Слайд 5Лекция 1 Средства анализа
Сущность такой методологии формально
Каждому алгоритму соответствует функция f(n),
Это означает, что в результате проведения экспериментов, время выполнения алгоритма А при любом размере входных данных n не превышает значения cn, где с является константой, определяемой условиями используемого аппаратного и программного обеспечения. Если имеются два алгоритма А и В, причем время выполнения алгоритма А пропорционально n, а время выполнения B пропорционально n2, то предпочтительнее использовать алгоритм А, так как функция n возрастает медленнее, чем функция n2.
Для того, чтобы применять данную методику без реализации алгоритма, рассмотрим высокоуровневые системы описания алгоритмов (раздел 3.2), и необходимые базовые математические положения (раздел 3.3).
Слайд 6Лекция 1 Средства анализа
Часто программистам удобно описывать алгоритм в форме, наиболее
Псевдокод
Слайд 7Лекция 1 Средства анализа
3.2.1. Пример псевдокода
Нахождение максимума в массиве - поиск
Псевдокод алгоритма arrayМах
Алгоритм arrayМах(A, n):
Input: массив A, содержащий n целых чисел (n>1).
Output: элемент с максимальным значением в массиве A.
currentMax←А[0]
for i←1 to n-1 do
if currentMax < A[i] then
currentMax←A[i]
return currentMax
Фрагмент кода 3.1. Алгоритм arrayМах
Слайд 8Лекция 1 Средства анализа
public class ArrayMaxProgram
{ /** находит элемент с максимальным
* содержащем n целых чисел.
*/
static int arrayMax(int[ ] A, int n)
{ int currentMax = A[0]; // выполняется один раз
for (int i=1; i < n; i++) // выполняется от 1 до n,
// n-1 раз соответственно.
if (currentMax < A[i]) // выполняется n-1 раз
currentMax = A[i]; //выполняется максимально n-1 раз
return currentMax; // выполняется один раз
}
public static void Main()
{ int[ ] num = { 10, 15, 3, 5, 56, 107, 22, 16, 85 };
int n = num.Length;
Console.WriteLine("Array:");
for (int i=0; i < n; i++) Console.WriteLine(" " + num[i]);
Console.WriteLine(".");
Console.WriteLine("Максимальный элемент - "+arrayMax(num, n));
}
}
Алгоритм arrayMax в виде C#-программы. В комментариях указано, сколько раз выполняются определенные команды в ходе выполнения программы
Псевдокод выглядит компактнее C#-кода, и его легче читать и понимать
Слайд 9Лекция 1 Средства анализа
Что такое псевдокод
Псевдокод - сочетание естественного языка и
Выражения (арифметические и логические) - используются стандартные математические символы.
Знак ← применяется в качестве оператора присваивания (оператор «=» языка C#).
Знак «=» - отношение равенства в логических выражениях (оператор «==» языка C#).
Объявление метода. Конструкция имя_алгоритма (param1, param2, ...) объявляет метод с его параметрами.
Структуры принятия решений. if условие then действия [else действия]. Отступы используются для обозначения выполняемых в том или другом случае действий.
Цикл while условие do действия.
Цикл repeat действия until условие.
Цикл for. for — описание переменной и инкремента, do действия.
Индексирование массива. A[i] обозначает i-ую ячейку массива А. Ячейки массива А с количеством ячеек n индексируются от А[0] до А[n-1].
Обращения к методам, object.method (args) (часть object необязательна, если она очевидна).
Возвращаемое методом значение. Значение return. Данный оператор возвращает значение, указанное в методе, вызывающим данный метод.
Написание псевдокода состоит в поиске баланса между общим и частным; такое умение вырабатывается в ходе практической деятельности.
Описание алгоритма должно начинаться с краткого абстрактного объяснения характера входных и выходных данных, а также основных действий и используемых идей алгоритма.
Слайд 10Лекция 1 Средства анализа
1. Записать алгоритм в виде кода одного из
2. Перевести программу в последовательность машинных команд (или команд промежуточного языка, используемых в виртуальной машине C#).
3. Определить для каждой машинной команды i время ti, необходимое для ее выполнения.
4. Определить для каждой машинной команды i количество повторений ni этой команды i за время выполнения алгоритма.
5. Определить произведение tt*ni, для всех машинных команд, что и будет составлять время выполнения алгоритма.
Данный подход позволяет точно определить время выполнения алгоритма, однако очень сложен, поскольку требуется доскональное знание машинных команд, создаваемых компилятором и средой, в которой выполняется алгоритм.
Аналитический (формальный)подход к анализу алгоритмов
Слайд 11Лекция 1 Средства анализа
Удобнее проводить анализ программы, написанной на псевдокоде. Выделим
присваивание переменной значения,
вызов метода,
выполнение арифметической операции (например, сложение двух чисел),
сравнение двух чисел,
индексация массива,
переход по ссылке на объект,
возвращение из метода.
Примем предположение, что время выполнения различных простейших операций приблизительно одинаково. Теперь достаточно подсчитать количество таких операций и использовать полученное значение в качестве критерия оценки времени выполнения алгоритма. Такой подсчет количества операций можно соотнести со временем выполнения алгоритма в условиях определенного аппаратного и программного обеспечения. Таким образом, число t простейших операций, выполняемых внутри алгоритма, пропорционально действительному времени выполнения данного алгоритма.
Слайд 12Лекция 1 Средства анализа
Подсчет числа простейших операций для алгоритма arrayМах.
Данный анализ
Инициализация переменной currentMax значением А[0] – две операции (индексация массива и присваивание переменной значения).
В начале выполнения цикла for счетчик i получает значение 1. Это соответствует одной операции.
Перед выполнением тела цикла проверяется условие i
При возвращении значения переменной currentMax однократно выполняется одна операция.
Итак, число простейших операций t(n), выполняемых алгоритмом аrrауМах, минимально равно 2+1+n+4(n-1)+1=5n, если А[0] является максимальным элементом массива,
а максимально
2+1+n+6(n-1)+1=7n-2 если элементы массива отсортированы по возрастанию.
Слайд 13Лекция 1 Средства анализа
Анализ средних и худших показателей
К сожалению, проведение анализа
В связи с этим в дальнейшем будем по умолчанию указывать худший показатель времени выполнения алгоритма (если не будет оговорено другое условие). Можно сказать, что в худшем случае алгоритм arrayMax выполняет t(n)=7n-2 простейших операций.
Подобный тип анализа намного проще анализа средних показателей, так как не требует использования теории вероятности; для него просто необходимо определить, при каком типе исходных данных время выполнения алгоритма будет максимальным, что зачастую является вполне очевидным. Кроме того, использование такого подхода может способствовать совершенствованию алгоритмов. Другими словами, если создаваемый алгоритм должен успешно работать при худших исходных данных, предполагается, что он будет работать при любом типе исходных данных.
Слайд 14Лекция 1 Средства анализа
Асимптотическая нотация
Очевидно, что анализ времени выполнения такого простого
Возвращаясь к алгоритму arrayMax, упрощенный анализ даст следующий результат: алгоритм выполняет от 5n до 7n-2 шагов при размере исходных данных n.
Зачастую достаточно просто знать, что время выполнения алгоритма, например, arrayMax, увеличивается пропорционально n. Это означает, что действительное время выполнения алгоритма является произведением n на некий постоянный множитель, который определяется условиями аппаратного и программного обеспечения, и может колебаться в определенных пределах в зависимости от особенностей исходных данных.
Формализуем приведенный метод анализа структур данных и алгоритмов, используя математический подход.
Слайд 15Лекция 1 Средства анализа
Нотация большого О
Пусть f(n) и g(n) являются функциями,
Пример 3.6: 7n-2 есть О(n).
Доказательство: по определению нотации большого О необходимо найти действительную константу с>0, а также целочисленную константу n0>1. Одним из очевидных вариантов является с=7, а n0=1. Безусловно, это один из бесконечного множества вариантов; с в данном случае может принимать значение любого действительного числа, равного или большего 7, а n0 - любое целочисленное значение, большее или равное 1.
Нотация большого О позволяет выразить, что функция f «меньше или равна» другой функции g (в определении это выражается знаком «≤») до определенного постоянного значения (константа с в определении) и по мере того, как n стремится к бесконечности (условие «n>n0» в определении).