Олеговна
Студентка 3 курса
Специальность 230701 «Прикладная информатика (по отраслям)»
Научный руководитель:
Мирзоева Эльвира Ровшановна
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Создание программы для решения линейных, квадратных и биквадратных уравнений презентация
Содержание
- 1. Создание программы для решения линейных, квадратных и биквадратных уравнений
- 2. Актуальность работы Данная работа актуальна тем, что
- 3. Цель работы Цель работы – создание программы
- 4. Задачи Для достижения поставленной цели были поставлены
- 5. ООП Объектно-ориентированное программирование (ООП) — это способ
- 6. Линейное уравнение Линейным уравнением называется уравнение вида:
- 7. Квадратное уравнение Квадратное уравнение —
- 8. Биквадратное уравнение Биквадратным называется уравнение вида ax
- 9. Анализ технического задания Техническое задание: разработать приложение,
- 10. Анализ технического задания Проанализировав техническое задание, целесообразно
- 11. Анализ технического задания После выбора типа уравнения,
- 12. Работа программы Рассмотрим работу программы на примере решение квадратного уравнения x2-26x+120=0
- 13. Работа программы
- 14. Работа программы
- 15. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 1Создание программы для решения линейных, квадратных и биквадратных уравнений.
Выполнила: Витенко Екатерина
Слайд 2Актуальность работы
Данная работа актуальна тем, что решение линейных, квадратных и биквадратных
уравнений является сложной и длительной работой, и поэтому программа создана для того, чтобы упростить вычисления пользователю.
Слайд 3Цель работы
Цель работы – создание программы для нахождения корней уравнения. В
данном случае линейного, квадратного и биквадратного.
Слайд 4Задачи
Для достижения поставленной цели были поставлены следующие задачи:
Изучение различных источников по
необходимому программному обеспечению (Delphi);
Проектирование интерфейса программы;
Разработка программного кода приложения;
Тестирование и отладка созданного продукта;
Составление эксплуатационной документации приложения.
Проектирование интерфейса программы;
Разработка программного кода приложения;
Тестирование и отладка созданного продукта;
Составление эксплуатационной документации приложения.
Слайд 5ООП
Объектно-ориентированное программирование (ООП) — это способ организации кода в программе путем
его группировки в виде объектов, то есть отдельных элементов, которые включают информацию (значения данных) и функции.
Объектно-ориентированный язык программирования позволяет создавать различные приложения, с интерфейсом, понятным для пользователя. Это удобная среда для создания различных математических программ.
Слайд 6Линейное уравнение
Линейным уравнением называется уравнение вида: ax+b=c, где a — коэффициент
при неизвестной, b — свободный член (любое число). Решить уравнение значит найти такое число (корень уравнения), что при подстановке его вместо переменной x , получается верное равенство.
Слайд 7Квадратное уравнение
Квадратное уравнение — это уравнение вида ax 2+bx+c
= 0 , где коэффициенты a , b и c — любые действительные числа, причем а ≠ 0 . Корнями квадратного уравнения называют такие значения переменной, при которых квадратное уравнение обращается в верное числовое равенство. Решить квадратное уравнение — значит найти все его корни или установить, что корней нет.
Слайд 8Биквадратное уравнение
Биквадратным называется уравнение вида ax 4 + bx 2 +
c =0 , где a <> 0. Биквадратное уравнение решается методом введения новой переменной: положив x 2 = y , придем к квадратному уравнению ay 2 + by + c =0 .
Слайд 9Анализ технического задания
Техническое задание: разработать приложение, которое находит корни линейного, квадратного
и биквадратного уравнений. Пользователь выбирает, какое из трех представленных уравнений ему предстоит решить. Далее он вводит значения переменных, и программа выводит ему результаты.
Слайд 10Анализ технического задания
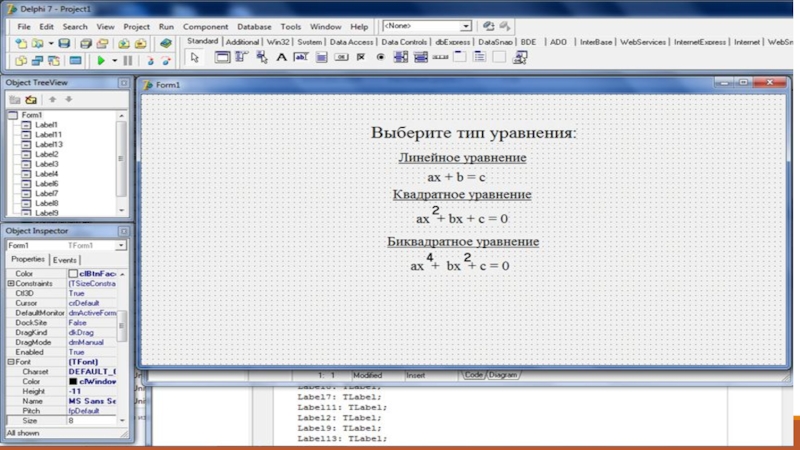
Проанализировав техническое задание, целесообразно оформить решение в виде формы,
на которой будут расположены кнопки выбора типа уравнения: «Линейное уравнение», «Квадратное уравнение», «Биквадратное уравнение».
Слайд 11Анализ технического задания
После выбора типа уравнения, открывается новая форма, в которую
вводятся исходные данные, и производится вычисление нажатием на кнопку «Вычислить».