- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления (Лекция 02) презентация
Содержание
- 1. Системы счисления (Лекция 02)
- 2. КРУГЛЫЕ ЧИСЛА «Из подъезда вышел человек лет
- 3. КРУГЛЫЕ ЧИСЛА Говоря о круглых числах, мы
- 4. КРУГЛЫЕ ЧИСЛА (7)10=(10)7 (49)10=(72)10=(100)7 (147)10=(3*72)10=(300)7 (10)10=(13)7 10
- 5. СИСТЕМЫ СЧИСЛЕНИЯ СИСТЕМА СЧИСЛЕНИЯ - СОВОКУПНОСТЬ ПРИЕМОВ ПРЕДСТАВЛЕНИЯ, ОБОЗНАЧЕНИЯ НАТУРАЛЬНЫХ ЧИСЕЛ.
- 6. СИСТЕМЫ СЧИСЛЕНИЯ ПОЗИЦИОННЫЕ НЕПОЗИЦИОННЫЕ
- 7. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ В позиционных системах счисления
- 8. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ ОСНОВАНИЕ СИСТЕМЫ СЧИСЛЕНИЯ -
- 9. ИСТОРИЯ Первоначальный аппарат счета, причина победы десятичной системы счисления в процессе исторического развития
- 10. ДРУГИЕ СИСТЕМЫ СЧИСЛЕНИЯ Двенадцатеричная система счисления: Дюжина=двенадцать
- 11. ПОЧЕМУ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ ИСПОЛЬЗУЕТСЯ ДВОИЧНАЯ СИСТЕМА
- 12. ПОЧЕМУ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ ИСПОЛЬЗУЮТСЯ ВОСЬМЕРИЧНАЯ И
- 13. ПЕРЕВОД ВОСЬМЕРИЧНЫХ И ШЕСТНАДЦАТЕРИЧНЫХ ЧИСЕЛ В ДВОИЧНУЮ
- 14. ПЕРЕВОД ИЗ ДВОИЧНОЙ СИСТЕМЫ В ВОСЬМЕРИЧНУЮ ИЛИ
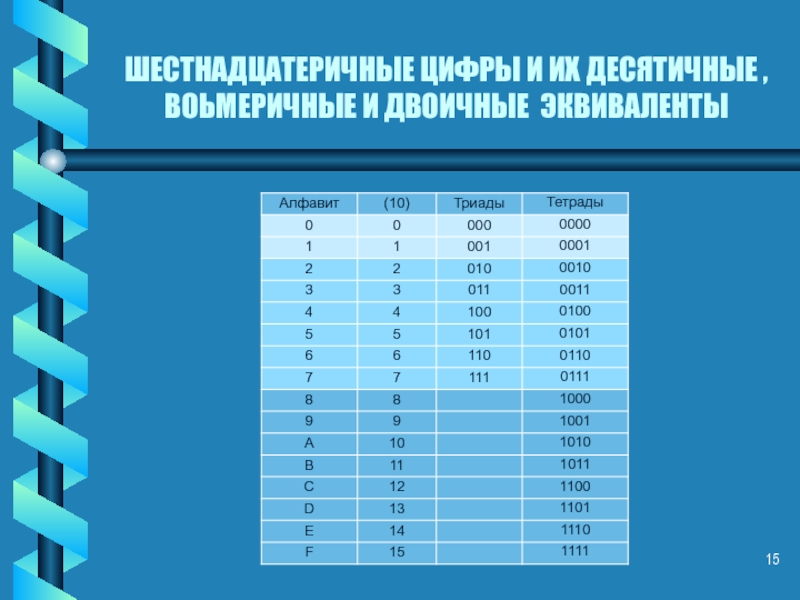
- 15. ШЕСТНАДЦАТЕРИЧНЫЕ ЦИФРЫ И ИХ ДЕСЯТИЧНЫЕ , ВОЬМЕРИЧНЫЕ И ДВОИЧНЫЕ ЭКВИВАЛЕНТЫ
- 16. ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ШЕСТНАДЦАТЕРИЧНУЮ
- 17. ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ШЕСТНАДЦАТЕРИЧНУЮ
- 18. ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ВОСЬМЕРИЧНУЮ
- 19. ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ВОСЬМЕРИЧНУЮ
- 20. ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ШЕСТНАДЦАТЕРИЧНУЮ
- 21. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Теорема. Пусть q -
- 22. ПЕРЕХОД К СИСТЕМЕ СЧИСЛЕНИЯ С ДРУГИМ ОСНОВАНИЕМ
- 23. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Пример: Переведем число
- 24. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ ПРЕДСТАВЛЕНИЕ ПРАВИЛЬНЫХ ДРОБЕЙ В
- 25. ПЕРЕХОД К СИСТЕМЕ СЧИСЛЕНИЯ С ДРУГИМ ОСНОВАНИЕМ
- 26. ЛИТЕРАТУРА Фомин С. В. - Системы счисления. М.: Наука. 1987. 48 с.
Слайд 2КРУГЛЫЕ ЧИСЛА
«Из подъезда вышел человек лет около 49, пройдя по улице
(неточная цитата из книги С.В. Фомина «Системы счисления»)
Когда мы оцениваем какую-то величину — возраст человека, расстояние и т. п. — приблизительно, то мы всегда пользуемся круглыми числами и говорим обычно «метров 150», «человек лет 50» и т. п.
Круглыми числами проще оперировать, чем некруглыми, их легче запомнить, с ними удобней производить арифметические действия. Например, ни для кого не составит труда умножить в уме 100 на 200, если же нужно перемножить два некруглых трехзначных числа, скажем 147 и 343, то далеко не всякий сделает это без карандаша и бумаги.
Слайд 3КРУГЛЫЕ ЧИСЛА
Говоря о круглых числах, мы обычно не отдаем себе отчета
Чтобы разобраться в этом вопросе, посмотрим прежде всего, что представляет собой наша обычная десятичная система счисления, которой мы все пользуемся. В этой системе каждое целое положительное число представляется в виде суммы единиц, десятков, сотен и т. д., т. е. в виде суммы различных степеней числа 10 с коэффициентами, которые могут принимать значения от 0 до 9 включительно.
(2014)10 = 2*103+0*102+1*101+4*100
Слайд 4КРУГЛЫЕ ЧИСЛА
(7)10=(10)7
(49)10=(72)10=(100)7
(147)10=(3*72)10=(300)7
(10)10=(13)7
10 - круглое число, потому что оно принято за основание
Слайд 5СИСТЕМЫ СЧИСЛЕНИЯ
СИСТЕМА СЧИСЛЕНИЯ - СОВОКУПНОСТЬ ПРИЕМОВ ПРЕДСТАВЛЕНИЯ, ОБОЗНАЧЕНИЯ НАТУРАЛЬНЫХ ЧИСЕЛ.
Слайд 7ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
В позиционных системах счисления вес цифры
(т. е. ее
Арабская система счисления - позиционная:
9999 – веса цифры «9» различны.
Римская система счисления - непозиционная:
LXXXII - восемьдесят два
(L в любой позиции пятьдесят,
Х в любой позиции десять,
I в любой позиции один).
Слайд 8ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
ОСНОВАНИЕ СИСТЕМЫ СЧИСЛЕНИЯ - количество символов (цифр), используемых для
Обозначение: q - основание системы счисления.
Если q =10, то используются цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
(651)10 = 6*102+5*101+1*100
(651)7 = (6*72+5*71+1*70)10=(336)10
Слайд 9ИСТОРИЯ
Первоначальный аппарат счета, причина победы десятичной системы счисления в процессе исторического
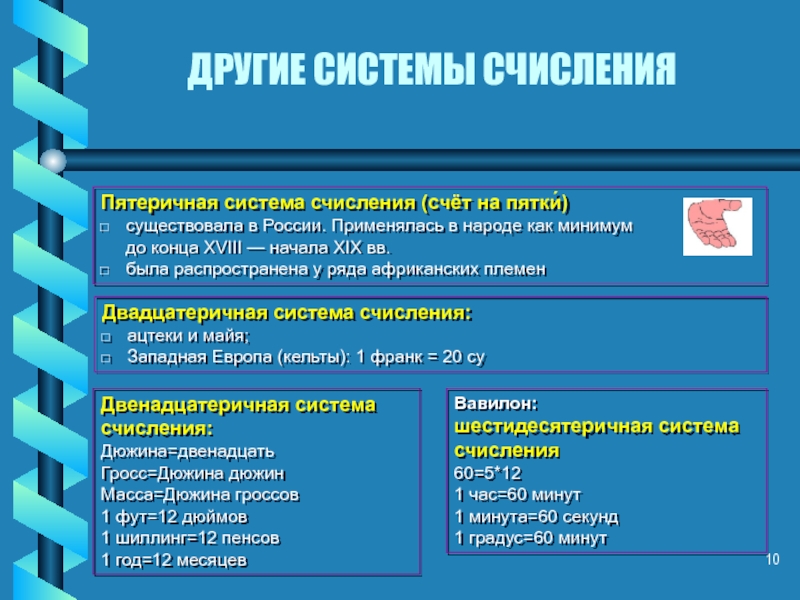
Слайд 10ДРУГИЕ СИСТЕМЫ СЧИСЛЕНИЯ
Двенадцатеричная система счисления:
Дюжина=двенадцать
Гросс=Дюжина дюжин
Масса=Дюжина гроссов
1 фут=12 дюймов
1 шиллинг=12 пенсов
1
Пятеричная система счисления (cчёт на пятки́)
существовала в России. Применялась в народе как минимум
до конца XVIII — начала XIX вв.
была распространена у ряда африканских племен
Вавилон:
шестидесятеричная система счисления
60=5*12
1 час=60 минут
1 минута=60 секунд
1 градус=60 минут
Двадцатеричная система счисления:
ацтеки и майя;
Западная Европа (кельты): 1 франк = 20 су
Слайд 11ПОЧЕМУ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ ИСПОЛЬЗУЕТСЯ ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ?
двоичная система счисления реализуется
представление информации посредством только двух состояний надежно и помехоустойчиво;
возможно применение булевой алгебры для выполнения логических преобразований информации;
двоичная арифметика намного проще десятичной.
Недостаток двоичной системы счисления: длинная запись числа
Слайд 12ПОЧЕМУ В ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ ИСПОЛЬЗУЮТСЯ ВОСЬМЕРИЧНАЯ И ШЕСТНАДЦАТЕРИЧНАЯ
СИСТЕМЫ СЧИСЛЕНИЯ?
От этих
Эти системы счисления ближе к десятичной и поэтому более удобны для человека;
Запись чисел в этих системах короче, чем в двоичной.
Слайд 13ПЕРЕВОД ВОСЬМЕРИЧНЫХ И ШЕСТНАДЦАТЕРИЧНЫХ ЧИСЕЛ В ДВОИЧНУЮ СИСТЕМУ
Так как основания
ПЕРЕВОД ВОСЬМЕРИЧНЫХ И ШЕСТНАДЦАТЕРИЧНЫХ ЧИСЕЛ В ДВОИЧНУЮ СИСТЕМУ: каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) для восьмеричных чисел или тетрадой (четверкой цифр) для шестнадцатеричных чисел.
Слайд 14ПЕРЕВОД ИЗ ДВОИЧНОЙ СИСТЕМЫ
В ВОСЬМЕРИЧНУЮ ИЛИ ШЕСТНАДЦАТЕРИЧНУЮ
Чтобы перевести число из двоичной
Если крайние триады (тетрады) оказались неполными, они дополняются нулями в целой части числа – слева, в дробной части (после запятой) - справа.
Слайд 16ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ШЕСТНАДЦАТЕРИЧНУЮ И ОБРАТНО
Пример 1:
↓ ↓ ↓ ↓
0011 0101 1100 0111 (тетрады)
↓ ↓ ↓ ↓
3 5 C 7 16
110101110001112 = 35С716
Пример 2:
1 0 A 16
↓ ↓ ↓
0001 0000 1010 (тетрады)
↓ ↓ ↓
1 0000 1010 2
10A16 = 1000010102
Слайд 17ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ШЕСТНАДЦАТЕРИЧНУЮ И ОБРАТНО
Пример 3:
В7, А16=
Пример 4:
11110,12 = 0001 1110,10002=1Е,816
Слайд 18ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ВОСЬМЕРИЧНУЮ И ОБРАТНО
Пример 5:
10 101 000 111 2
↓ ↓ ↓ ↓
010 101 000 111 (триады)
↓ ↓ ↓
2 5 0 7 8
101010001112
Пример 6:
1 0 7 8
↓ ↓ ↓
001 000 111 (триады)
↓ ↓ ↓
1 000 111 2
1078 = 10001112
Слайд 19ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ВОСЬМЕРИЧНУЮ И ОБРАТНО
Пример 7:
4011,258=100 000
Пример 8:
10110,12=010 110,1002=26,48
Слайд 20ПРЕОБРАЗОВАНИЕ ИЗ ДВОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ШЕСТНАДЦАТЕРИЧНУЮ И ОБРАТНО
Упражнение:
Выполнить перевод, используя
1110110,12 = ?8;
1010001012 = ?16;
40118 = ?2;
СВ7,916 = ?2
Слайд 21ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Теорема. Пусть q - натуральное число, q >1. Тогда
N = anqn + an-1qn-1 + ... + a1q1 + a0q0,
где для любого n an∈ {0,1,…,q-1};
q - основание системы счисления;
anan-1…a1a0 - запись натурального числа в системе счисления с основанием q.
В системе счисления с основанием q для записи чисел требуется q цифр, одна из которых ноль.
Слайд 22ПЕРЕХОД К СИСТЕМЕ СЧИСЛЕНИЯ С ДРУГИМ ОСНОВАНИЕМ ДЛЯ НАТУРАЛЬНЫХ ЧИСЕЛ q1→
Число делится нацело на q2 , затем полученное частное на q2 , и т. д., пока деление возможно (частное≥ q2 ).
Последнее частное и остатки, начиная с последнего, образуют запись числа в системе счисления с основанием q2 .
Деление выполняется в системе с основанием q1.
Пример:
2010 = 101002
Проверка:
101002 = 1*24 + 0*23 + 1*22 + 0*21 + 0*20 = 16+4 = 2010
Слайд 23ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Пример:
Переведем число 75 из десятичной системы в двоичную,
Ответ: 7510 = 1 001 0112 = 1138 = 4B16
Слайд 24ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
ПРЕДСТАВЛЕНИЕ ПРАВИЛЬНЫХ ДРОБЕЙ В СИСТЕМЕ СЧИСЛЕНИЯ С ОСНОВАНИЕМ q:
D=
0,2510=2*(1/10)+5*(1/10)2
Дробь - нормализованная, если a-1≠0
Слайд 25ПЕРЕХОД К СИСТЕМЕ СЧИСЛЕНИЯ С ДРУГИМ ОСНОВАНИЕМ ДЛЯ ПРАВИЛЬНЫХ ДРОБЕЙ q1→
0,312510=0,248
Умножаем дробь на q2 , затем дробную часть произведения на q2 , и т. д., пока не будет достигнуто требуемое число знаков или пока дробная часть произведения не станет равной нулю. Умножение выполняется в системе счисления с основанием q1 .