- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления. Двоичная система счисления презентация
Содержание
- 1. Системы счисления. Двоичная система счисления
- 2. Система счисления – это знаковая система, в
- 3. Системы счисления Непозиционные Позиционные Десятичная СС
- 4. 6 2 3 0 12 -
- 5. Перевод целых чисел из
- 6. Развернутая запись числа Десятичная СС Двоичная СС
- 7. Сложение Умножение Вычитание Деление
- 8. Для того чтобы лучше освоить двоичную систему
- 9. Правила сложения: 0+0=0 1+0=1 0+1=1 1+1=10 (результат
- 10. 10110 1001
- 11. Правила умножения: 0*0=0 1*0=0 0*1=0 1*1=1 Умножение
- 13. Правила вычитания: 0-0=0 1-0=1 1-1=0 10-1=1(из нуля
- 14. 1011 1001 11-1011=
- 15. Деление в двоичной системе счисления выполняется, как
Слайд 2Система счисления – это знаковая система, в которой числа записываются по
Системы счисления
Непозиционные
Позиционные
В позиционных системах счисления количественное значение цифры зависит от её позиции в числе.
В непозиционных системах счисления количественное значение цифры не зависит от её позиции в числе
5
7
9
5
7
9
XI (11) дописывая цифру справа от числа, прибавляем её
IX (9) дописывая цифру слева от числа, отнимаем её
I - один
X - десять
- сотни
- десятки
- единицы
Слайд 3Системы счисления
Непозиционные
Позиционные
Десятичная СС
0..9
Двоичная СС
0, 1
Восьмеричная СС
0..7
Шестнадцатеричная СС
0..9, А, В, С, D, E, F
В позиционных СС основание системы равно количеству цифр (знаков в её алфавите) и определяет во сколько раз различаются значения одинаковых цифр, стоящих в соседних позициях
Римская СС
I – один
V – пять
X – десять
L – пятьдесят
C – сто
D – пятьсот
M – тысяча
Египетская СС
Греческая СС
Слайд 46
2
3
0
12
-
6
2
26
13
2
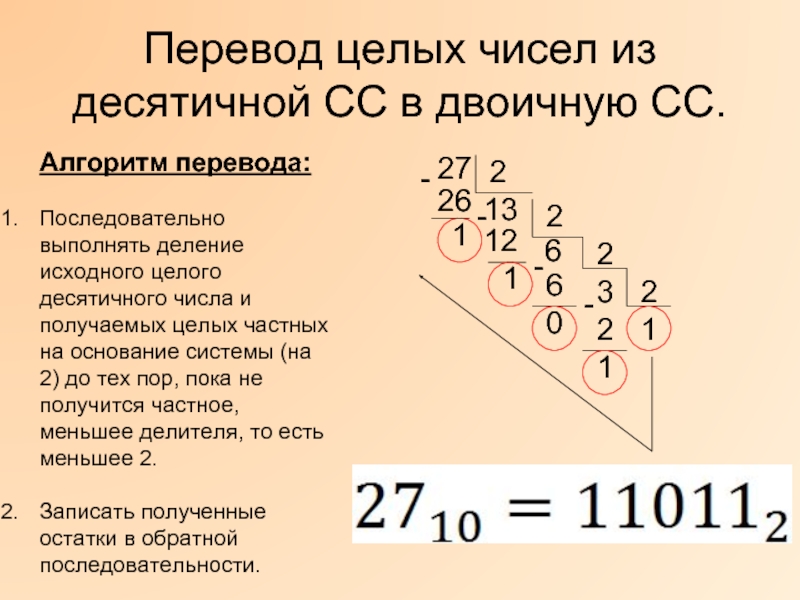
Перевод целых чисел из десятичной СС в двоичную СС.
Алгоритм перевода:
Последовательно выполнять
Записать полученные остатки в обратной последовательности.
27
-
1
1
-
2
-
2
1
1
Слайд 5
Перевод целых чисел из двоичной СС в десятичную СС.
=
Алгоритм перевода:
Двоичное число
Произвести вычисления.
0
1
2
3
4
5
6
7
Слайд 8Для того чтобы лучше освоить двоичную систему счисления, необходимо освоить выполнение
Все позиционные системы счисления”одинаковы”, а именно, во всех них арифметические операции выполняются по одним и тем же правилам:
справедливы одни и те же законы арифметики: коммутативный, ассоциативный, дистрибутивный;
справедливы правила сложения, вычитания, умножения и деления столбиком;
Правила выполнения арифметических операций опираются на таблицы сложения и умножения.
Слайд 9Правила сложения:
0+0=0
1+0=1
0+1=1
1+1=10 (результат сложения двух единиц: ноль и единица переноса в
Сложение
Слайд 10 10110 1001
+ 101 + 1010 + 1 + 1,11
11011 10011 10000 111 ,001
Сложение двоичных чисел выполняются в столбик.
Слайд 12 1011
*101 *11
+ 1011 1101
1011 +1101
110111 100111
Умножение двоичных чисел производится в столбик аналогично умножения десятичных чисел:
Слайд 13Правила вычитания:
0-0=0
1-0=1
1-1=0
10-1=1(из нуля вычесть единицу нельзя, поэтому для вычитания необходимо занять
Вычитание
Слайд 141011 1001 11-1011= -(1011-11)
-111
100 11 - 11
1000
При выполнении операции вычитания всегда из большего по абсолютной величине вычитается меньшее и у результата ставится соответствующий знак.
Слайд 15Деление в двоичной системе счисления выполняется, как и в десятичной системе.
Пример:
- 111 11
1 11
- 1 11
0
Деление