- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы логических уравнений в задачах ЕГЭ по информатике презентация
Содержание
- 1. Системы логических уравнений в задачах ЕГЭ по информатике
- 2. Постановка задачи (ЕГЭ-2011) 2011: Решаемость 3,2% Сколько решений имеет система уравнений:
- 3. Методы решения замена переменных последовательное подключение уравнений
- 4. Аналогии с алгеброй Алгебра Логика Элементарные уравнения:
- 5. Формулы логики – I A. Свойства
- 6. Формулы логики – II Б. Дизъюнкция
- 7. Формулы логики – III В. Импликация Определение импликации Свойства импликации
- 8. Формулы логики – IV Г. Эквивалентность Представление через базис:
- 9. Основные идеи Решение системы уравнений – это
- 10. Типичные ограничения Задача 1. «соседние
- 11. Типичные ограничения Задача 3. «запрещена комбинация 10»
- 12. Более сложный пример Задача 4. «запрещена комбинация
- 13. Более сложный пример Задача 5. «запрещена комбинация 00»
- 14. Более сложный пример нет 00! непересекающиеся множества!
- 15. Более сложный пример 1, 1,
- 16. Ещё пример Задача 6. «запрещена комбинация 1→0»
- 17. И снова – рекуррентные уравнения
- 18. Последний пример Задача 7. Последовательность выполнения:
- 19. Демо-вариант ЕГЭ-2017 Группировка по вертикали:
- 20. Демо-вариант ЕГЭ-2017 Решение: 000000, 000001, 000011, 000111,
- 21. Демо-вариант ЕГЭ-2017 Уравнение связи: без ограничений! Ограничения:
- 22. Демо-вариант ЕГЭ-2017 X: 000000 000001 000011 000111
- 23. Демо-вариант ЕГЭ-2016 Замена переменных: Решения:
- 24. Демо-вариант ЕГЭ-2016 Решения: Z = 010101010,
- 25. Демо-вариант ЕГЭ-2015 «запрещено 00» «после
- 26. Демо-вариант ЕГЭ-2015 Варианты отличаются местом
- 27. Демо-вариант ЕГЭ-2014
- 28. Демо-вариант ЕГЭ-2014 «очередной бит равен хотя
- 29. Демо-вариант ЕГЭ-2013
- 30. Демо-вариант ЕГЭ-2013 5 решений: X =
- 31. Демо-вариант ЕГЭ-2013 X: 0000 0001 0011 0111
- 32. Демо-вариант ЕГЭ-2012 Замена переменных:
- 33. Демо-вариант ЕГЭ-2012 К одному уравнению: Решения:
- 34. Демо-вариант ЕГЭ-2012 Переход к исходным переменным: 5 бит 5 бит
- 35. Ещё одна задача (2015) Замена переменных:
- 36. Ещё одна задача (2015) Решение: «запрещена комбинация
- 37. Ещё одна задача (2015) 2 решения: (0;1)
- 38. И ещё одна задача (2015) Запрещены комбинации: Запрещено 01x!
- 39. И ещё одна задача (2015) запрещено 01x
- 40. Пробное тестирование (2015) Замена переменных: Решения: 010101, 101010 «биты чередуются»
- 41. Ещё одна задача (2016) В другой форме: Ограничения
- 42. Ещё одна задача (2016) Ограничение: Запрещено: (0,0)
- 43. Основные шаги решения упрощение уравнений с помощью
- 44. Как можно рассказать детям?
- 45. Как можно рассказать детям (II)?
- 46. Как можно рассказать детям (III)? Демо-2016 Пробное тестирование
- 47. Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель
Постановка задачи (ЕГЭ-2011) 2011: Решаемость 3,2% Сколько решений имеет система уравнений:
Слайд 3Методы решения
замена переменных
последовательное подключение уравнений
метод отображения (Е.А. Мирончик)
«Информатика. Первое сентября»
1. Е.
А. Мирончик, Метод отображения // Информатика, № 10, 2013, с. 18-26.
2. Е.А. Мирончик, Люблю ЕГЭ за В15, или Еще раз про метод отображения // Информатика, № 7-8, 2014, с. 26-32.
2. Е.А. Мирончик, Люблю ЕГЭ за В15, или Еще раз про метод отображения // Информатика, № 7-8, 2014, с. 26-32.
трудоёмко
длинная запись решения
2012: Решаемость 13,2%
Слайд 4Аналогии с алгеброй
Алгебра
Логика
Элементарные уравнения: линейные, квадратные.
Элементарные уравнения не выделяются.
Методы преобразования: законы
сложения и умножения, формулы сокращенного умножения, свойства степеней.
Методы преобразования: законы логики (см. далее).
Обычно уравнение имеет одно или несколько решений.
Уравнение может иметь большое, но конечное число решений.
Слайд 6
Формулы логики – II
Б. Дизъюнкция и конъюнкция
Сочетательный закон
Переместительный закон
Закон повторения
Распределительный закон
Правила
де Моргана
Слайд 9Основные идеи
Решение системы уравнений – это битовая цепочка (битовый вектор)
Битовый вектор
рассматривается как единый объект.
Уравнения – это ограничения на битовый вектор (ограничения на комбинации битов).
Нужно выделить элементарные уравнения и записать ограничения «на русском языке».
Количество решений находится по правилам комбинаторики.
Уравнения – это ограничения на битовый вектор (ограничения на комбинации битов).
Нужно выделить элементарные уравнения и записать ограничения «на русском языке».
Количество решений находится по правилам комбинаторики.
Слайд 10Типичные ограничения
Задача 1.
«соседние биты одинаковы»
Решения: 00000, 11111
Задача 2.
«соседние биты различны»
Решения: 01010,
10101
«биты чередуются»
Слайд 11Типичные ограничения
Задача 3.
«запрещена комбинация 10»
Решения: 000000, 000001, 000011, 000111,
001111, 011111, 111111
«после первой единицы все следующие биты – 1»
«все нули, потом все единицы»
Для уравнения с N переменными: N+1 решений.
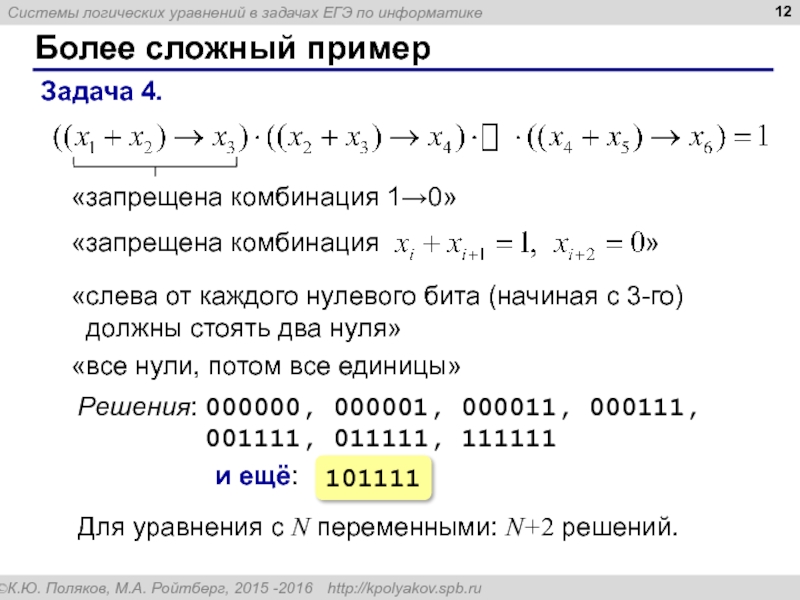
Слайд 12Более сложный пример
Задача 4.
«запрещена комбинация 1→0»
Решения: 000000, 000001, 000011, 000111,
001111, 011111, 111111
«слева от каждого нулевого бита (начиная с 3-го)
должны стоять два нуля»
«все нули, потом все единицы»
Для уравнения с N переменными: N+2 решений.
Слайд 16Ещё пример
Задача 6.
«запрещена комбинация 1→0»
«после двух единиц подряд следуют только единицы»
Слайд 17И снова – рекуррентные уравнения
Структура решения:
«хвост»
«голова»
нет комбинации 11
последний бит – 0
Слайд 18Последний пример
Задача 7.
Последовательность выполнения:
запрещена комбинация 1→0 на последнем шаге
Начальное значение:
Решения уравнения
… = 0.
Слайд 20Демо-вариант ЕГЭ-2017
Решение:
000000, 000001, 000011, 000111, 001111, 011111, 111111
000000, 000001, 000011, 000111,
001111, 011111, 111111
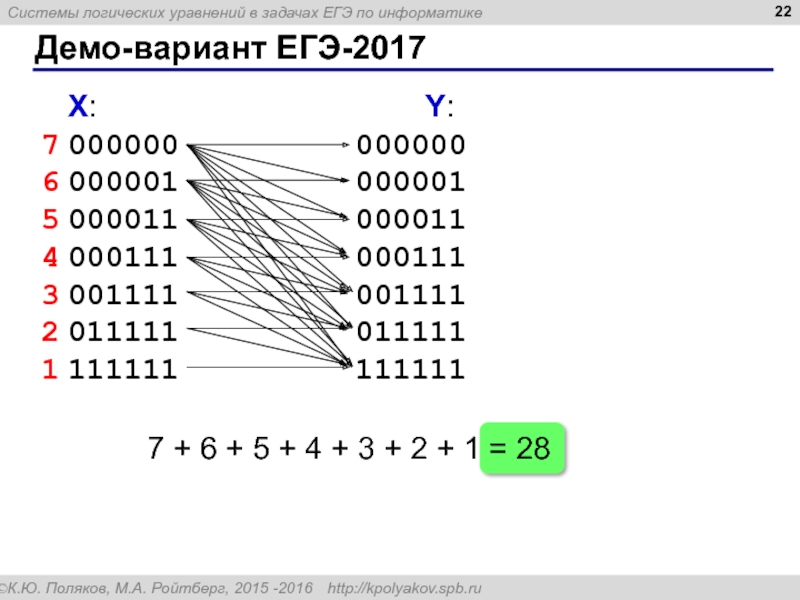
Слайд 22Демо-вариант ЕГЭ-2017
X:
000000
000001
000011
000111
001111
011111
111111
Y:
000000
000001
000011
000111
001111
011111
111111
7
6
5
4
3
2
1
7 + 6 + 5 + 4 + 3 +
2 + 1 = 28
Слайд 25
Демо-вариант ЕГЭ-2015
«запрещено 00»
«после двух единиц идут только единицы»
«хвост»
«голова»
«запрещено 00 и 11»
«биты
чередуются»
Слайд 26
Демо-вариант ЕГЭ-2015
Варианты отличаются местом последнего нуля:
11111111, 01111111, 10111111, 01011111, 10101111,
01010111,
10101011, 01010101, 10101010
1 решение
2 решения
01011111
2 нулевых бита, 22 вариантов
Слайд 28
Демо-вариант ЕГЭ-2014
«очередной бит равен хотя бы одному из 2-х следующих»
«запрещены комбинации
100 и 011»
сначала цепочка нулей, потом биты чередуются (1/0)
сначала цепочка единиц, потом биты чередуются.
0000000000
0000000001
0000000010
0000000101
…
0101010101
1111111111
1111111110
1111111101
1111111010
…
1010101010
10 + 10 = 20
«после 01 или 10 биты чередуются»
Слайд 30Демо-вариант ЕГЭ-2013
5 решений:
X = 0000, 0001, 0011, 0111, 1111
5 решений:
Y = 0000, 0001, 0011, 0111, 1111
без ограничений!
Связь X и Y:
Слайд 31Демо-вариант ЕГЭ-2013
X:
0000
0001
0011
0111
1111
Y:
0000
0001
0011
0111
1111
5
4
3
2
1
5 + 4 + 3 + 2 + 1 =
15
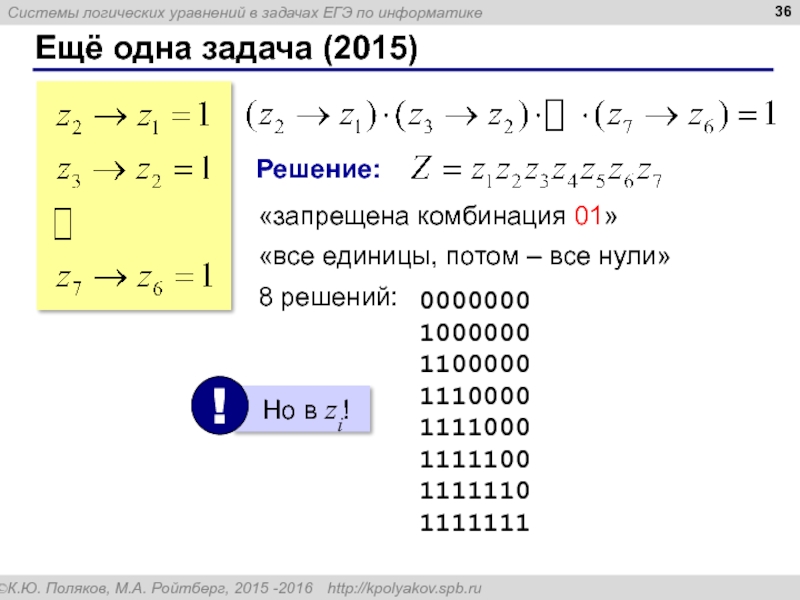
Слайд 36Ещё одна задача (2015)
Решение:
«запрещена комбинация 01»
«все единицы, потом – все
нули»
8 решений:
0000000
1000000
1100000
1110000
1111000
1111100
1111110
1111111
Слайд 37Ещё одна задача (2015)
2 решения: (0;1) и (1;0)
1 решение: (1;1)
0000000
1000000
1100000
1110000
1111000
1111100
1111110
1111111
Z
Z
128
64
32
16
8
4
2
1
X,Y
X,Y
128 +
64 + 32 + 16 + 8 + 4 + 2 + 1 = 255
255
Слайд 39И ещё одна задача (2015)
запрещено 01x и 100
01 может стоять только
в конце после цепочки нулей или единиц
после цепочки 1 может стоять 0
после цепочки 1 может стоять 0
Все решения:
00...001
11...101
11...110
00...000
11...111
Слайд 42Ещё одна задача (2016)
Ограничение:
Запрещено:
(0,0)
(1,0) или (0,1)
X=11111111
стыкуется со всеми! (N+1 решений)
остальные –
только с равными и с Y=11111111!
(+2N решений)
(1,1)
Получим 10!
и
Если есть 0, то X=Y!
Слайд 43Основные шаги решения
упрощение уравнений с помощью эквивалентных преобразований
замена переменных (если возможно)
исследование
структуры всех решений («голова+хвост»)
подсчёт количества решений по формулам комбинаторики
подсчёт количества решений по формулам комбинаторики
Слайд 47Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г. Санкт-Петербург
kpolyakov@mail.ru
РОЙТБЕРГ Михаил Абрамович
д.ф.-м.н., зав. кафедрой АТП ФИВТ МФТИ, зам. руководителя Федеральной комиссии по разработке КИМ ЕГЭ по информатике и ИКТ mroytberg@lpm.org.ru
д.ф.-м.н., зав. кафедрой АТП ФИВТ МФТИ, зам. руководителя Федеральной комиссии по разработке КИМ ЕГЭ по информатике и ИКТ mroytberg@lpm.org.ru
