- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Синтез линейной системы управления презентация
Содержание
- 1. Синтез линейной системы управления
- 2. Содержание лекции Этапы синтеза алгоритма управления. Общий
- 3. Этапы синтеза алгоритма управления Синтез алгоритма включает
- 4. Общий алгоритм расчета управления Рис.
- 5. Формирование цели и эталонной модели Линейное управление
- 6. Формирование цели и эталонной модели Параметр tпп*
- 7. Формирование цели и эталонной модели Аналогичным образом
- 8. Формирование цели и эталонной модели
- 9. Нахождение стабилизирующего управления
- 10. Компенсация возмущения
- 11. Вычисление задающего воздействия
- 12. Пример
Слайд 1Синтез линейной системы управления
Проектирование систем управления роботов. Синтез управления
Бессекерский В.А., Попов
Пшихопов В.Х., Медведев М.Ю., Костюков В.А., Гайдук А.Р., Федоренко Р.В., Гуренко Б.В., Крухмалев В.А., Медведева Т.Н. Проектирование роботов и робототехнических систем: Учебное пособие – Ростов-на-Дону: Изд-во ЮФУ, 2014 – 196 с.
А.Р. Гайдук, В.Е. Беляев, Т.А. Пьявченко. Теория автоматического управления в примерах и задачах с решениями в Matlab. Учебник для ВУЗов. СПб. Издательство Лань. 2011. ISBN 978-5-8114-1255-6.
Слайд 2Содержание лекции
Этапы синтеза алгоритма управления.
Общий алгоритм расчета управления.
Формирование цели и эталонной
Нахождение стабилизирующего управления.
Компенсация возмущения.
Вычисление задающего воздействия.
Пример.
Проектирование систем управления роботов. Синтез управления
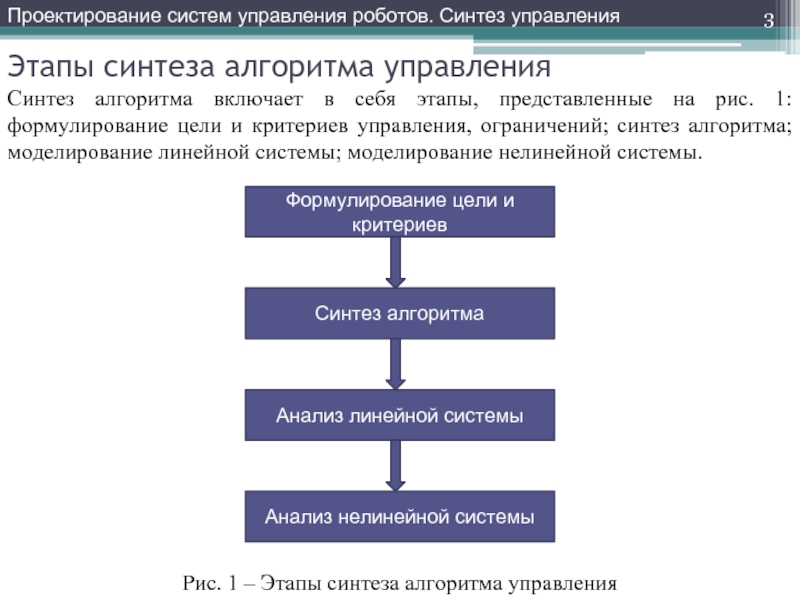
Слайд 3Этапы синтеза алгоритма управления
Синтез алгоритма включает в себя этапы, представленные на
Рис. 1 – Этапы синтеза алгоритма управления
Проектирование систем управления роботов. Синтез управления
Формулирование цели и критериев
Синтез алгоритма
Анализ линейной системы
Анализ нелинейной системы
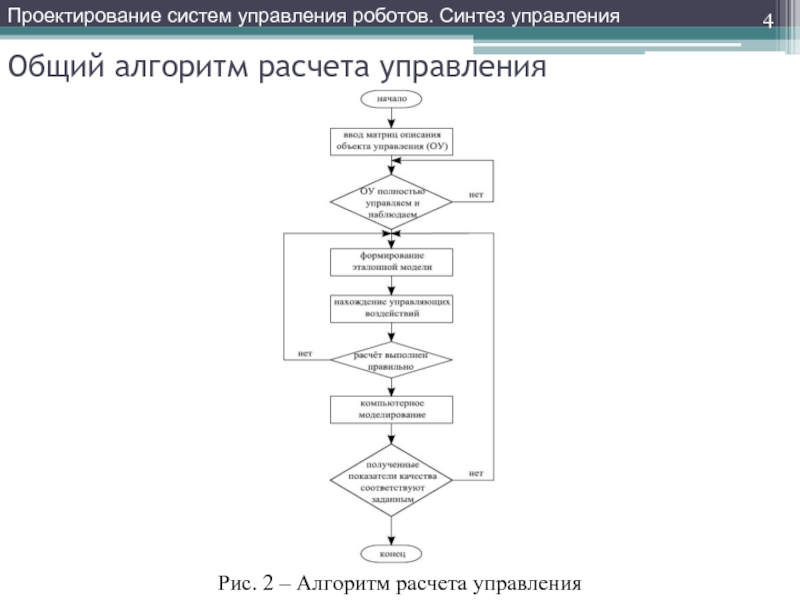
Слайд 4Общий алгоритм расчета управления
Рис. 2 – Алгоритм расчета управления
Проектирование систем управления
Слайд 5Формирование цели и эталонной модели
Линейное управление по состоянию и возмущениям базируется
(1)
Проектирование систем управления роботов. Синтез управления
В этой связи целью управления является стабилизация объекта (1) в нулевом положении равновесия.
В качестве исходных требований к системе управления используются время переходного процесса tпп, точность Δ и перерегулирование σ. На основе этих данных и порядка системы (1) формируется эталонный характеристический полином. В качестве эталонных полиномов используются стандартные характеристические полиномы, например, полином Ньютона или полином Баттерворта. Стандартный полином Ньютона формируется в виде
(2)
Из (2) следует, что характеристический полином Ньютона имеет один кратный действительный корень λ=-ω0. Параметр ω0 определяется из требований к времени переходного процесса tпп :
(3)
Время при ω0 =1
Требуемое время
Слайд 6Формирование цели и эталонной модели
Параметр tпп* либо получается путем моделирования, вычисляется
Проектирование систем управления роботов. Синтез управления
(4)
При моделировании требуется подать на передаточную функцию:
(5)
единичный скачок и зафиксировать время, когда переходная функция будет в пределах величины Δ от единицы. Полиномы Ньютона для различных порядков представлены в табл. 1.
Таблица 1 – Полиномы Ньютона
Слайд 7Формирование цели и эталонной модели
Аналогичным образом строятся полиномы Баттерворта, представленные в
Проектирование систем управления роботов. Синтез управления
Таблица 2 – Полиномы Баттерворта
(5)
При этом D(p) выбирается из таблицы 2 и параметр ω0 =1.
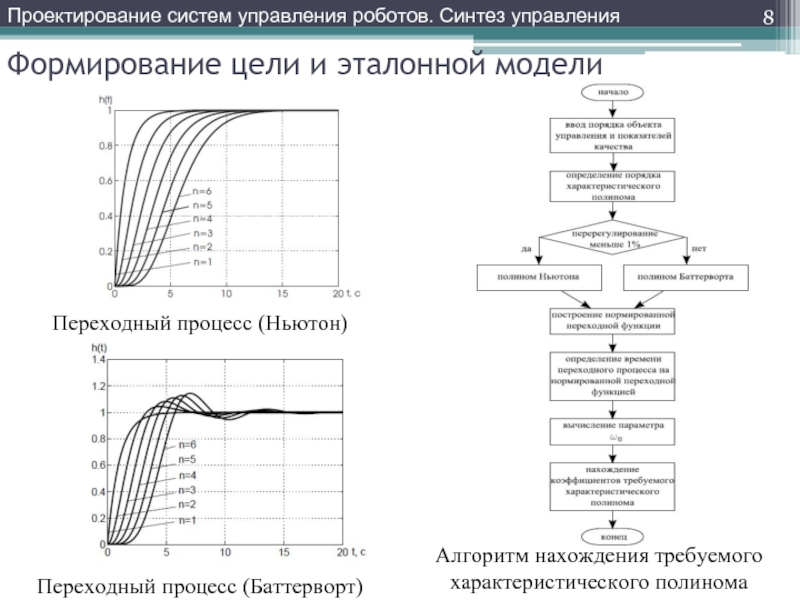
Слайд 8Формирование цели и эталонной модели
Проектирование систем управления роботов. Синтез управления
Алгоритм нахождения
Переходный процесс (Баттерворт)
Переходный процесс (Ньютон)
Слайд 9Нахождение стабилизирующего управления
Проектирование систем управления роботов. Синтез управления
Структура закона управления имеет
(6)
где K1, K2 – матицы постоянных коэффициентов, выбираемые в ходе синтеза; g – вектор задающих воздействий.
В ходе нахождения стабилизирующего управления, f и g полагаются нулевыми и ищется вектор K1.
Для подвижного объекта управляющим вектором являются управляющие силы и моменты, т.е. матрица B является единичной диагональной матрицей. В этой связи переходить к канонической управляемой форме для синтеза стабилизирующего управления не требуется.
Полагая в (1) и (6) f и g нулевыми, подставим (6) в (1)
(7)
Характеристическое уравнение системы (7) имеет вид
(8)
Далее, сравнивая коэффициенты при одинаковых степенях p в полиномах D(p) и D*(p), получаем линейную систему уравнений, из которых находим K1.
Слайд 10Компенсация возмущения
Проектирование систем управления роботов. Синтез управления
Подставим управление (6) в (1)
(9)
Чтобы
(10)
В общем случае, когда управление не воздействует непосредственно на переменную, к которой приложено возмущение, требуется найти передаточную функцию от возмущения к указанной переменной и выбрать коэффициенты матрицы K2 так, чтобы возмущение в установившемся режиме не влияло на указанную переменную.
Слайд 11Вычисление задающего воздействия
Проектирование систем управления роботов. Синтез управления
Для того, чтобы вычислить
(11)
В (11) x0 – вектор желаемых значений переменных состояния робота в установившемся режиме. Тогда вектор g равен
(12)
Слайд 12Пример
Проектирование систем управления роботов. Синтез управления
Рассмотрим линейную модель двигателя постоянного тока
Собственная
(13)
(14)
Управление имеет вид:
(15)
Подставим (15) в (13), полагая Mc и ωz равными нулю:
(16)
Слайд 13
Приводы роботов. Лекция 4
Пример
Характеристический полином системы (16) равен
(17)
Пусть желаемый характеристический полином
(18)
Сравнивая (17) и (18), находим выражения для коэффициентов управления
(19)
Тогда замкнутая система описывается уравнениями
(20)
Слайд 14
Пример
Приводы роботов. Лекция 4
Запишем ПФ системы (20) по моменту сопротивления
(21)
Выберем коэффициент
(22)
Выражение (15) содержит момент сопротивления, который редко измеряется. В этой связи отдельно строится наблюдатель момента сопротивления. Значение уставки wz вычислим из уравнений установившегося режима для замкнутой системы, приравняв производные к нулю: