Симуляції фазових переходів презентация

сплавах, кристалізація, рідина-скло, ......

Проблеми комп’ютерного моделювання ФП: скінчені розміри системи, похибка у визначенні температури ФП

Критичні показники (для магнетиків):

Спонтанна намагніченість

Намагніченість як функція поля h при T=Tc

Сприйнятливість

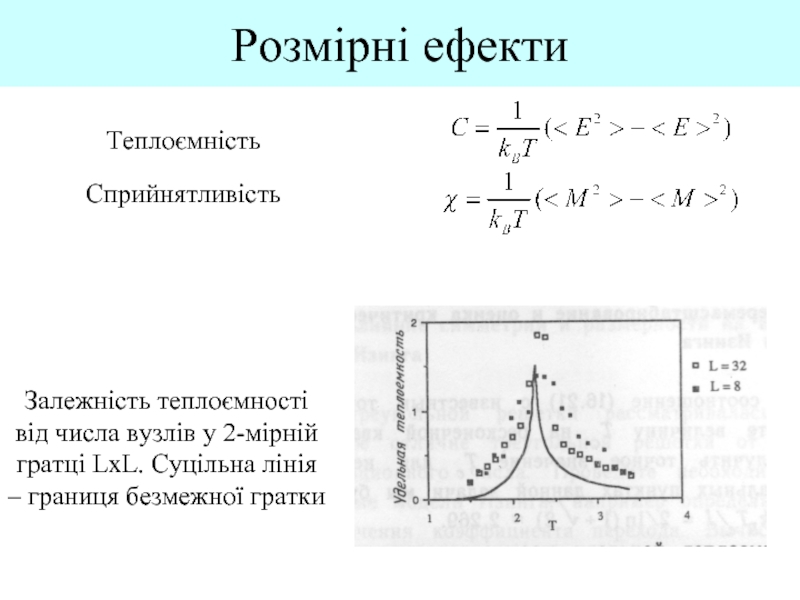
Питома теплоємність при h=0

найближчих сусідах

Завдання: порахувати намагніченість M як функцію температури.
Температура є зовнішнім параметром !!!

3-мірній гратці, розраховується її енергія взаємодії з найбдижчими сусідами
Перевернути спін даної частинки та розрахувати нову енергію пробної конфігурації
Прийняти переворот спіна з ймовірністю

METROPOLIS(SPIN,T,E,M)
CALL DATA(E,M,RESULTS)
ENDDO
CALL SAVE_OUTPUT(SPIN,RESULTS)
STOP
END

! ACCEPT
CALL MAGNETIZATION(SPIN,M)
ELSE
SPIN(IPX,IPY)=-SPIN(IPX,IPX) ! REJECT
ENDIF
RETURN
END

лінія – границя безмежної гратки

Теплоємність

Сприйнятливість

гратці будуть мати поведінку:

велика і конфігурації будуть статистично незалежні. Однак, в симуляціях на скінчених гратках залишається певна кореляція. Для її оцінки можна використати функції:

Якщо при N-му кроці така кореляція прямує до нуля, то для визначення середніх потрібно брати конфігурації через кожних N кроків

МК симуляцій для проміжних значень h

Напрям зовнішнього поля визначає напрям намагніченості

Зовнішнє поле розмиває криву намагніченості і приводить до ФП першого роду