- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Симплекс-метод для решения задач линейного программирования презентация
Содержание
- 1. Симплекс-метод для решения задач линейного программирования
- 2. Формулировка задачи Симплекс-метод Применение
- 3. Формулировка задачи Симплекс-метод Применение О
- 4. Формулировка задачи Симплекс-метод Применение О
- 5. Формулировка задачи Симплекс-метод Применение О
- 6. Формулировка задачи Симплекс-метод Применение О
- 7. Формулировка задачи Симплекс-метод Применение О
- 8. Формулировка задачи Симплекс-метод Применение О
- 9. Формулировка задачи Симплекс-метод Применение Теоретические
- 10. Формулировка задачи Симплекс-метод Применение Теоретические
- 11. Формулировка задачи Симплекс-метод Применение Теоретические
- 12. Формулировка задачи Симплекс-метод Применение Теоретические
- 13. Формулировка задачи Симплекс-метод Применение Теоретические
- 14. Формулировка задачи Симплекс-метод Применение Теоретические
- 15. Формулировка задачи Симплекс-метод Применение Теоретические
- 16. Формулировка задачи Симплекс-метод Применение Теоретические
- 17. Формулировка задачи Симплекс-метод Применение Теоретические
- 18. Формулировка задачи Симплекс-метод Применение Теоретические
- 19. Формулировка задачи Симплекс-метод Применение Теоретические
- 20. Формулировка задачи Симплекс-метод Применение Теоретические
- 21. Формулировка задачи Симплекс-метод Применение Теоретические
- 22. Формулировка задачи Симплекс-метод Применение Теоретические
- 23. Формулировка задачи Симплекс-метод Применение Теоретические
- 24. Формулировка задачи Симплекс-метод Применение Теоретические
- 25. Формулировка задачи Симплекс-метод Применение СМ
- 26. Формулировка задачи Симплекс-метод Применение СМ
Слайд 1
Формулировка задачи Симплекс-метод Применение
Симплекс-метод для решения задач линейного программирования
Слайд 2
Формулировка задачи Симплекс-метод Применение
Содержание
1.Формулировка задачи
О линейном программировании (ЛП) Математическая формулировка задачи
2.Cимплекс-метод (СМ)
Теоретические основы Геометрическая интерпретация Алгоритм СМ
3.Применение
СМ в различных типах задач ЛП
Реализация программы для решения симплекс-методом
Слайд 3
Формулировка задачи Симплекс-метод Применение
О линейном программировании Математическая формулировка задачи ЛП Графический
Что такое линейное программирование
Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.
Создатели линейного программирования Леонид Витальевич Канторович (1912-1986) Джордж Бернард Данциг (1914-2005)
Слайд 4
Формулировка задачи Симплекс-метод Применение
О линейном программировании Математическая формулировка задачи ЛП Графический
Три основных элемента задачи ЛП
Переменные
x¯ = (x1, . . . , xn)
Система линейных ограничений
.n
j=1 aijxj ≤ bi (i = 1 . . . m)
Целевая функция, которая подлежит оптимизации
j=1
f (x¯) = .n ci xj
Переменные в общем случае являются вещественными числами.
В системе ограничений может также присутствовать знак ” =”. Под оптимизацией понимается максимизация или минимизация целевой функции.
Симплекс-метод
4 / 28
Слайд 5
Формулировка задачи Симплекс-метод Применение
О линейном программировании Математическая формулировка задачи ЛП Графический
Основные теоремы ЛП
Теорема 1. Конечное оптимальное решение задачи ЛП должно соответствовать экстремальной (крайней) точке пространства решений.
Теорема 2. Базисные решения системы полностью определяют все её экстремальные точки.
Базис — m независимых векторов из числа n.
Экстремальные точки могут быть найдены путем вычисления допустимых базисных решений системы:
n!
m!(m−n)!
Симплекс-метод
5 / 28
Слайд 6
Формулировка задачи Симплекс-метод Применение
О линейном программировании Математическая формулировка задачи ЛП Графический
Общая линейная распределительная задача
Далее рассмотрим построение математической модели на примере следующей задачи.
Пусть имеется 3 вида сырья в количестве 45, 19, 10 единиц соответственно. Нужно изготовить продукцию 2-х видов с затратами 1, 3, 2 единиц сырья для продукции первого вида и 9, 3, 1 – для продукции второго вида соответственно. Прибыль от реализации продукции составляет 5 денежных единиц для продукции 1-го вида и 6 — для второго. Требуется найти такой план выпуска продукции из имеющегося сырья, при котором суммарная прибыль будет наибольшей.
Симплекс-метод
6 / 28
Слайд 7
Формулировка задачи Симплекс-метод Применение
О линейном программировании Математическая формулировка задачи ЛП Графический
Общая линейная распределительная задача
Запишем данные задачи в таблицу.
5x1 + 9x2 ≤ 45
3x1 + 3x2 ≤ 19
2x1 + 1x2 ≤ 10 при x1, x2 ≥ 0
f (˙x ) = 5x1 + 6x2 → max
Симплекс-метод
7 / 28
Слайд 8
Формулировка задачи Симплекс-метод Применение
О линейном программировании Математическая формулировка задачи ЛП Графический
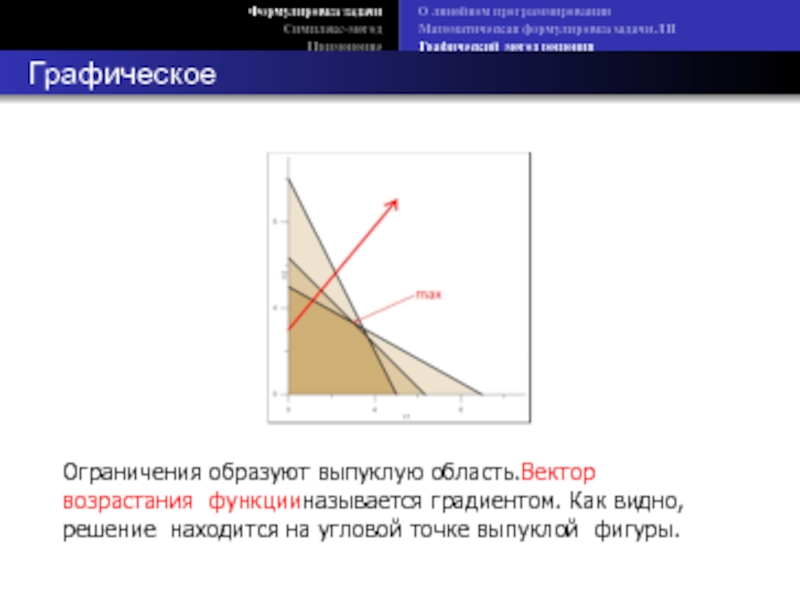
Графическое решение
Ограничения образуют выпуклую область.Вектор возрастания функцииназывается градиентом. Как видно, решение находится на угловой точке выпуклой фигуры.
Слайд 9
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
Каноническая система
Система ограничений
cвободный член в правой части не отрицателен
каждое уравнение содержит своё базисное неизвестное (входит в уравнение с коэффициентом +1, а в других уравнениях отсутствует)
Слайд 10
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
Дополнительные неизвестные
Необходимо привести
5x1 + 9x2 ≤ 45
3x1 + 3x2 ≤ 19
2x1 + 1x2 ≤ 10 при x1, x2 ≥ 0
f (˙x ) = 5x1 + 6x2 → max
Слайд 11
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
Дополнительные неизвестные
Теперь система
5x1 + 9x2 + x3 = 45
3x1 + 3x2 + x4 = 19
2x1 + 1x2 + x5 = 10
при x1, x2, x3, x4, x5 ≥ 0
f (˙x ) = 5x1 + 6x2 + 0 ∗ (x3 + x4 + x5) → max
Мамошкин А. М. (СПбГУ ИТМО КТ)
Симплекс-метод
http://rain.ifmo.ru/cat
11 / 28
Слайд 12
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
Основная идея
Решение общей
Находят любое решение (как правило, неоптимальное), удовлетворяющее ограничениям, или убеждаются, что решения не существует. Этот этап называется определением опорного плана (базиса).
Производится последовательное улучшение данного плана до получения оптимального. В некоторых задачах опорный план определяется легко, в противном случае используют специальные методы получения опорного плана (метод искусственного базиса).
Слайд 13
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
Графическая интерпретация симплекс-метода
Выпуклая
Слайд 14
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
Описание алгоритма СМ
1.Выражение
переменные: f (x ) = 5x1 + 6x2. Записать целевую функцию в форме Таккера: f (x ) = 0 − (−5x1 − 6x2).
2.Проверка базисного решения на оптимальность. 3.Проверка на наличие решения.
4.Выбор из небазисных переменных той, которая способна при введении её в базис увеличить значение целевой функции
5.Определение, какая из базисных переменных должна быть выведена из базиса.
Слайд 15
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
Описание алгоритма СМ
6.Выражение
7.Выражение остальных базисных переменных и целевой функции через новые небазисные переменные.
8.Повторение операций пунктов (2) - (7) до тех пор пока не будет найдено оптимальное решение.
Мамошкин А. М. (СПбГУ ИТМО КТ)
Симплекс-метод
http://rain.ifmo.ru/cat
15 / 28
Слайд 16
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
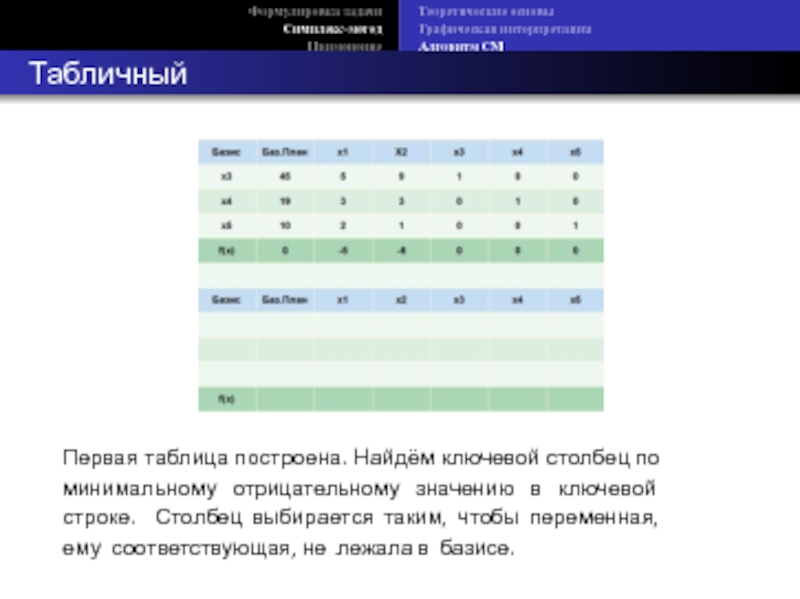
Табличный СМ
Первая таблица
Слайд 17
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
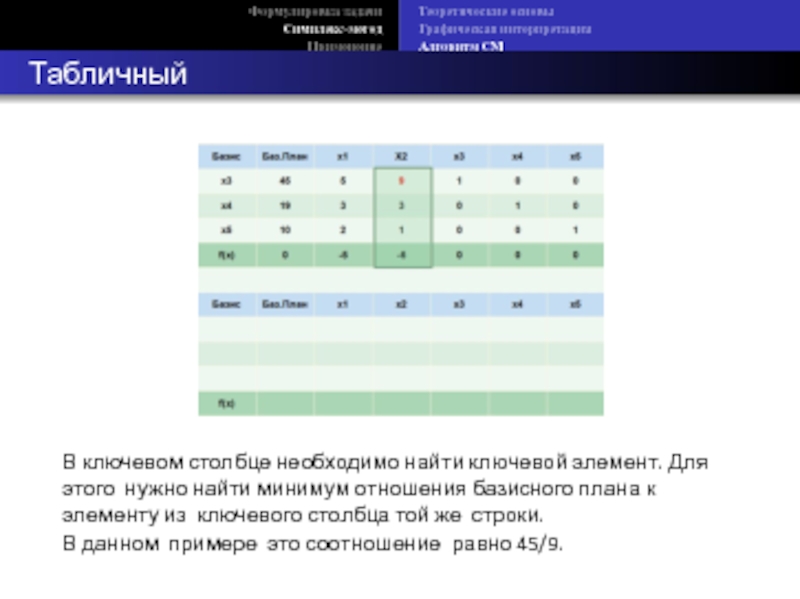
Табличный СМ
В ключевом
В данном примере это соотношение равно 45/9.
Слайд 18
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
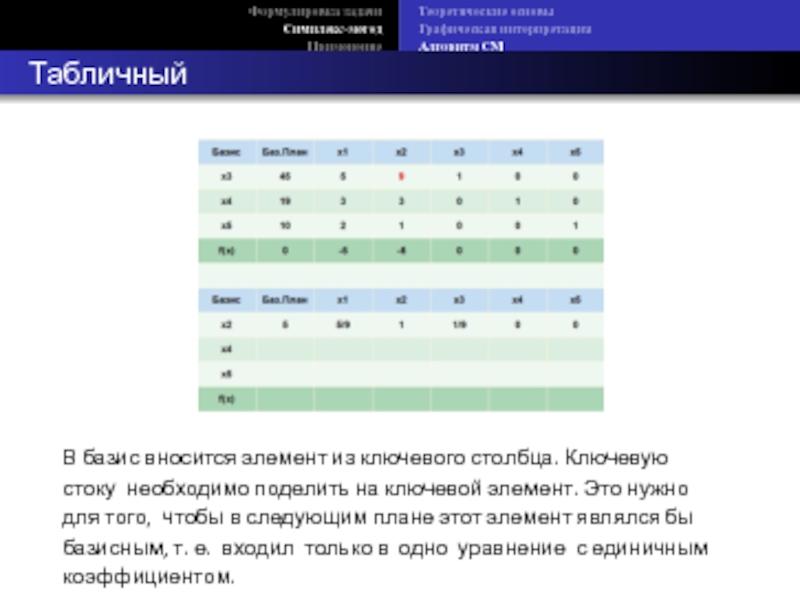
Табличный СМ
В базис
Слайд 19
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
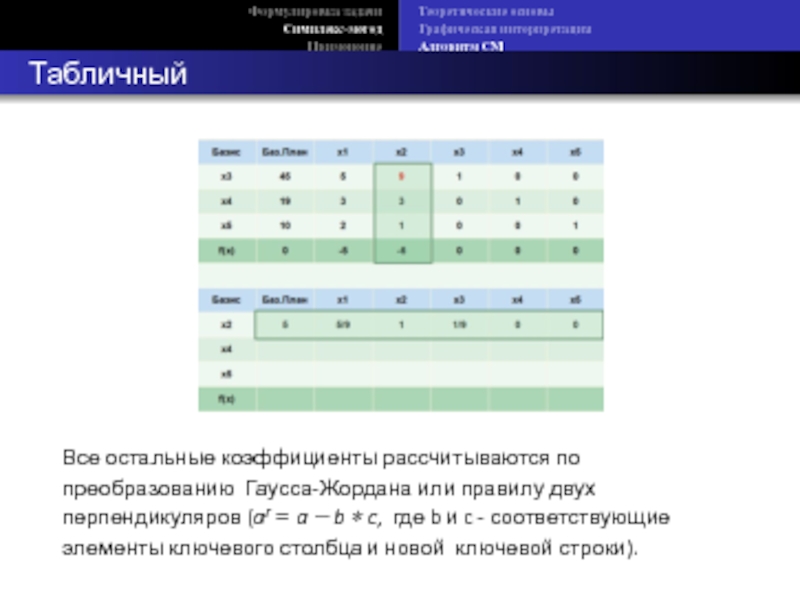
Табличный СМ
Все остальные
Слайд 20
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
Табличный СМ
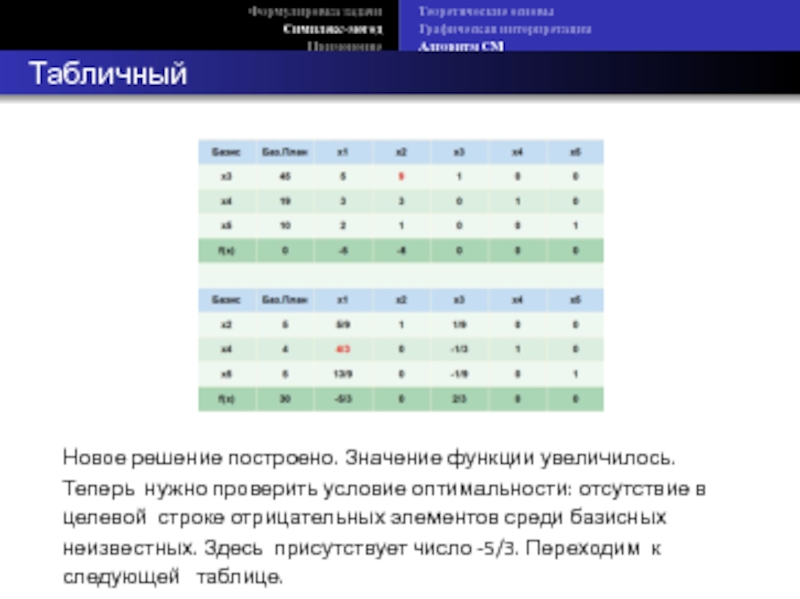
Новое решение
Слайд 21
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
Табличный СМ
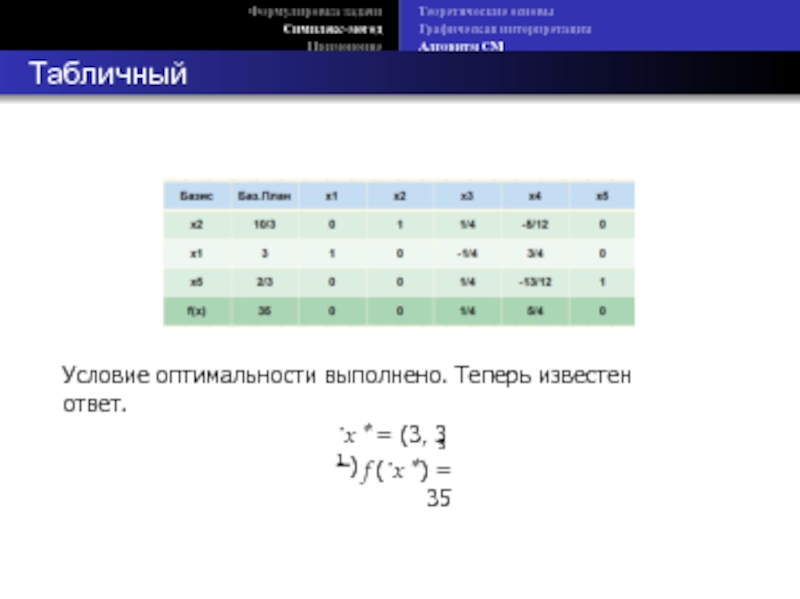
Условие оптимальности
˙x ∗ = (3, 3 1 )
3
f (˙x ∗) = 35
Слайд 22
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
Эффективность
Вычислительная эффективность СМ
машинного времени
В результате численных экспериментов получены результаты.
Число итераций при решении задач ЛП в стандартной форме с M ограничениями и N переменными заключено между M и 3M . Среднее число итераций 2M . Верхняя граница числа итераций равна 2M + N .
Требуемое машинное время пропорционально M 3. Число ограничений больше влияет на вычислительную эффективность, чем число переменных, поэтому при формулировке задач ЛП нужно стремиться к уменьшению числа ограничений пусть даже путём роста числа переменных
Слайд 23
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
Основные теоремы двойственности
Лемма
Лемма 2. Если f (x∗) = g (y∗) для некоторых планов x∗ и y∗ прямой и двойственной задач, то x∗ — это оптимальный план исходной задачи, а y∗ — это оптимальный план двойственной задачи.
Слайд 24
Формулировка задачи Симплекс-метод Применение
Теоретические основы Графическая интерпретация Алгоритм СМ
Основные теоремы двойственности
Теорема
Если одна из пары двойственных задач имеет оптимальный план, то и другая имеет оптимальный план и значение целевой функции задачи при их оптимальных планах равны между собой.
Если же целевая функция одной из пары двойственных задач не ограничена (для исходной задачи не ограничена сверху, а для двойственной задачи не ограничена снизу), то другая задача вообще не имеет планов.
Слайд 25
Формулировка задачи Симплекс-метод Применение
СМ в различных типах задач ЛП Реализация
Список источников
Применение
СМ универсален и с его помощью можно решить широкий спектр задач.
Максимальное паросочетание Максимальный поток Транспортная задача
Игра с нулевой суммой
Слайд 26
Формулировка задачи Симплекс-метод Применение
СМ в различных типах задач ЛП Реализация
Список источников
Список
Хемди А. Таха. Введение в исследование операций. — 7-е изд. — М. : Вильямс, 2007.
Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. — М. : Финансы и статистика, 1998.
Хачатрян С.Р., Пинегина М.В., Буянов В.П. Методы и модели решения экономических задач. — М. : Экзамен, 2005.