- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Симметричные криптосистемы. Лекция 1. Основные понятия и определения криптографии презентация
Содержание
- 1. Симметричные криптосистемы. Лекция 1. Основные понятия и определения криптографии
- 2. Часть 1 Симметричные криптосистемы Лекция 1. Основные понятия и определения криптографии
- 3. 1. Организация курса Слово криптография в переводе
- 4. Невозможно изучать стойкость криптосистем без рассмотрения методов
- 5. Для понимания материала, изложенного в настоящем пособии,
- 6. Основная терминология по курсу приведена в последующих
- 7. Программа курса Часть I. Симметричные криптосистемы
- 8. Основные методы криптоанализа блоковых шифров Элементы теории
- 9. способы построения и криптоанализ потоковых шифров на
- 10. Часть II. Криптосистемы с открытым ключом Идея
- 11. Генерирование простых чисел Важнейшие тесты по
- 12. Метод распределения ключей
- 13. Цифровые подписи с использованием КС ОК
- 14. Основная литература по курсу В.И.Коржик ,
- 15. Перечень основных лабораторных работ по курсу
- 16. Часть 2 1.Основы теории чисел 2.Тестирование простых
- 17. Отчетность по курсу Выполнение всех лабораторных работ . Экзамен по теоретическому курсу .
- 18. В результате освоения дисциплины студент должен
- 19. владеть: приемами проектирования типовых алгоритмов криптозащиты и
- 20. 2. Основные этапы исторического развития криптографии
- 21. Количество пользователей, использующих криптографическую защиту
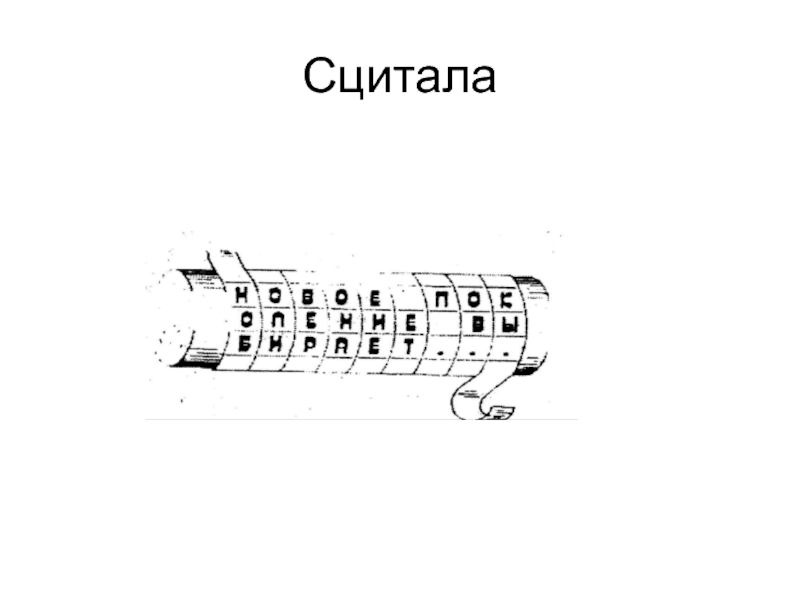
- 22. Сцитала
- 23. Шифр Цезаря: Mi→Mi+1 Защита информации
- 24. Шифр Виженера Нумерация символов русского алфавита Ei=Мi +Кi Защита информации ПриветПриветПривет чсвлшу….
- 25. Основные виды криптографических преобразований ∙ Шифрование
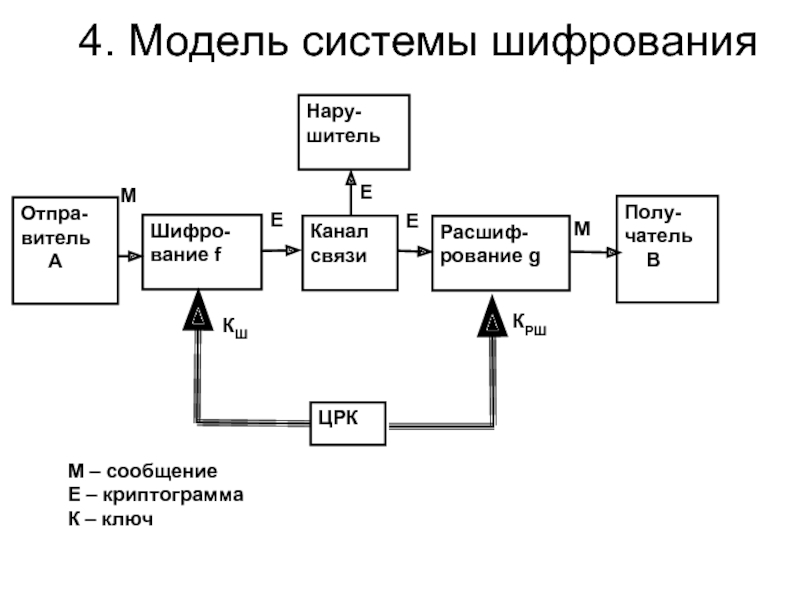
- 26. 4. Модель системы шифрования М – сообщение Е – криптограмма К – ключ
- 27. Описание модели шифрования
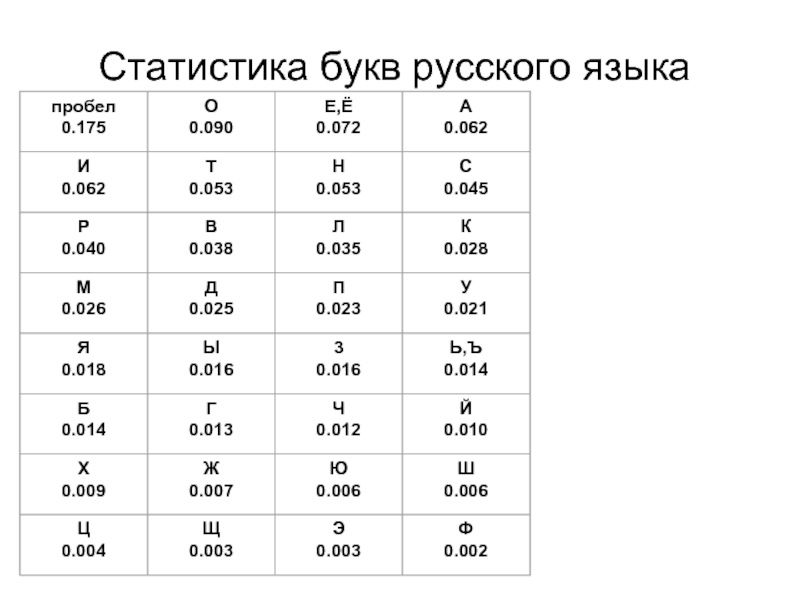
- 28. Статистика букв русского языка
- 29. Основные уравнения системы шифрования En=f(Mn,KNш)- уравнение шифрования Mn=g(En,KNрш)- уравнение дешифрования
- 30. Принцип Керхгоффа Согласно этому
- 31. Типы криптосистем По типу ключа криптосистемы
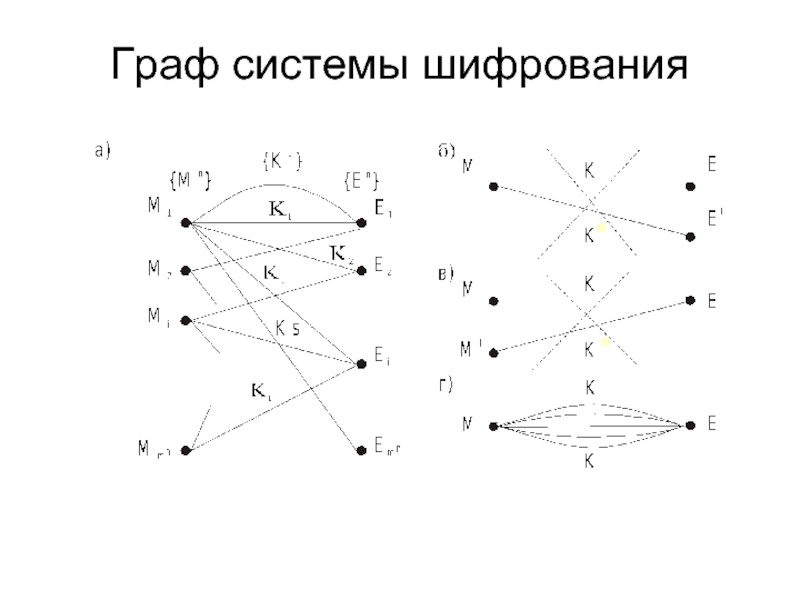
- 32. Граф системы шифрования
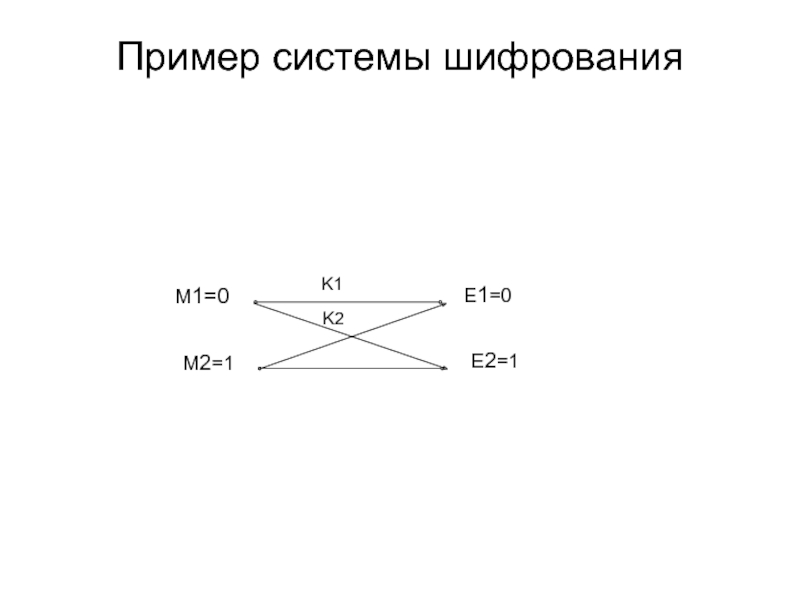
- 33. Пример системы шифрования M1=0 M2=1 E1=0 E2=1 K1 K2
- 34. Стойкость систем шифрования Стойкость - способность противостоять
- 35. Атаки нарушителя 1. Криптоанализ ведется, только на основе,
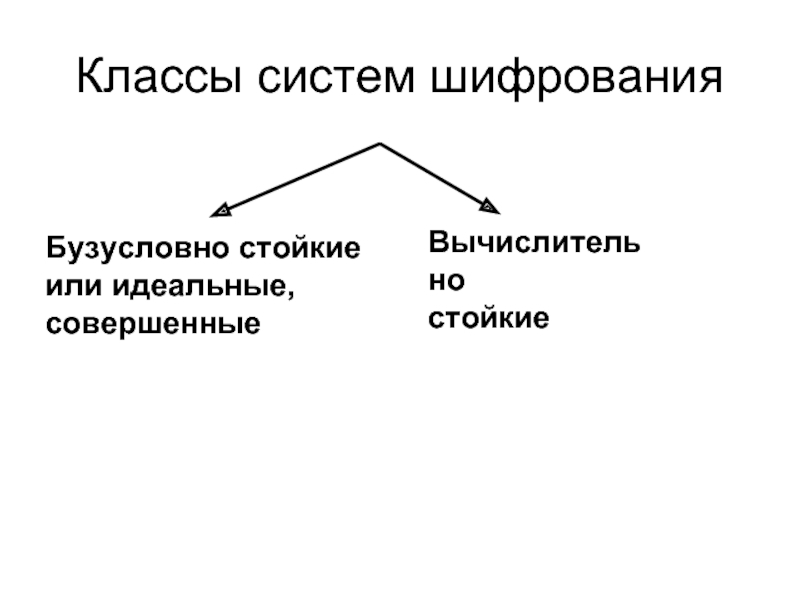
- 36. Классы систем шифрования Бузусловно стойкие или идеальные, совершенные Вычислительно стойкие
- 37. Безусловно стойкие (идеальные) системы шифрования Безусловно
- 38. Эквивалентное определение БССШ шенноновская информация в криптограмме
- 39. =
- 40. Пример идеальной КС
- 41. Вычислительно стойкие системы шифрования Система шифрования называется
- 42. Сложность алгоритмов криптоанализа должна соответствовать
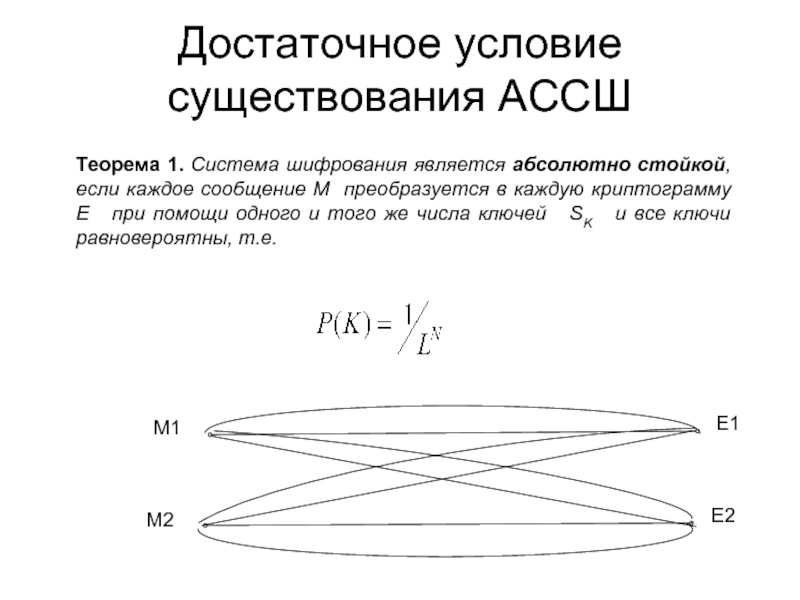
- 43. Достаточное условие существования АССШ Теорема 1. Система
- 44. Условия существования АССШ Следствие.
- 45. Пример расчета длины ключа для БССШ Параметра
- 46. Понятие расстояния единственности Ключ (длина L) Криптограмма
- 47. Пример расчета расстояния единственности Для русского языка
- 48. Статистика букв русского языка
Слайд 1Дисциплина:
Основы криптографии
Подготовил
д.т.н. профессор кафедры ЗСС
Яковлев Виктор Алексеевич
E-mail:viyak@bk.ru
Слайд 31. Организация курса
Слово криптография в переводе с греческого означает тайное письмо.
Задача курса “Основы криптографии” состоит в изложении основных понятий современной криптографии в ориентации на студентов, обучающихся по направлению 210700.62 «Инфокоммуникационные технологии и системы связи» , Профиль №2
При обучении по этому направлению не ставится задача подготовить будущих профессиональных криптографов, а с другой стороны, это не является поверхностным изложением основных определений и параметров современных криптосистем. Обучаемые должны усвоить их основные функции, возможные способы нападения на них со стороны злоумышленников, а также принципы построения современных алгоритмов шифрования, аутентификации и обеспечения целостности сообщений.
Слайд 4Невозможно изучать стойкость криптосистем без рассмотрения методов их криптоанализа (т. е. дешифрования
Значительное внимание в курсе уделяется побочным атакам на шифры, поскольку они часто не требуют для своего пояснения привлечения серьезного математического аппарата, однако пренебрежение этими атаками приводит к простому дешифрованию криптосистем без знания ключа.
Курс состоит из двух частей, . Первая часть посвящена традиционной (симметричной или одноключевой) криптографии, включая также некоторые вопросы аутентификации. Вторая часть посвящена несимметричной (двухключевой) криптографии, называемой иначе криптографией с открытым ключом, а также вопросам выполнения цифровой подписи и криптографических протоколов.
Слайд 5Для понимания материала, изложенного в настоящем пособии, достаточно знаний по курсам
Знания, полученные студентами на лекциях, закрепляются ими в ходе компьютерных лабораторных работ, которые охватывают абсолютно все разделы курса и построены таким образом, чтобы студенты смогли достаточно свободно варьировать параметрами криптосистем и исследовать вопросы именно криптографии, не отвлекаясь на составление программ.
Слайд 6Основная терминология по курсу приведена в последующих разделах. Здесь же будет
- законные (или легальные) пользователи криптосистемы, которые обладают секретными ключами, и незаконные (или нелегальные) пользователи, которые не обладают этими ключами и стремятся их найти, а также прочитать зашифрованное сообщение или нарушить его целостность (т. е. подделать его или фальсифицировать авторство), а также нарушить секретность выполняемых протоколов,
-криптоаналитиком будем называть пользователя, который пытается разработать методы для нарушения секретности криптосистемы. (Заметим, что криптоаналитик не обязательно является недружественным пользователем, поскольку он может применять свои методы для проверки стойкости существующих или разрабатываемых легальных криптосистем).
-взломом или атакой на криптосистему будем называть попытку дешифрования (криптоанализа) криптосистемы без знания ключа или попытку подделки цифровой подписи , а также нарушения секретности криптопротокола .
-нарушитель называется пассивным, если он только пытается прочитать сообщение, и активным, если он стремится изменить (подделать) сообщение или криптопротокол.
При подготовке куса использовано учебное пособие В.И.Коржик , В.П.Просихин , “Основы криптографии “, Линк, 2008.
Слайд 7Программа курса
Часть I. Симметричные криптосистемы
Модель криптосистемы
Принцип Керхгоффа
Типы криптосистем
Влияние ошибок в
Идеальные (безусловно стойкие) КС
Необходимые и достаточные условия для построения идеальных КС
КС с единственным и неединственным дешифрованием сообщений при заданной криптограмме. Расстояние единственности
Вывод формулы расстояния единственности для произвольного шифра
Пояснения к теореме Шеннона–Хеллмана
Вычислительно стойкие шифры
Способы построения вычислительно стойких блоковых шифров и их криптоанализ
Принцип построения блоковых шифров
Схема Фейстеля
Подстановочно-перестановочные шифры (ППШ)
Слайд 8Основные методы криптоанализа блоковых шифров
Элементы теории конечных полей [8, 9]
Модификации блоковых
Многократное шифрование
Примеры практически используемых блоковых шифров DES,AES,RC. ГОСТ 28147-89
Слайд 9способы построения и криптоанализ потоковых шифров на основе использования линейных рекуррентных
Линейный рекуррентный регистр и его основные свойства
Нелинейные узлы усложнения, используемые для построения потоковых шифров
Построение датчика шифрующей гаммы на основе использования ЛРР с управляемым тактированием
Основные способы криптоанализа потоковых шифров
Пример практически используемого в стандарте GSM потокового шифра A5/1
Аутентификация сообщений:
Общая структура (техника) аутентификации
Классификация систем аутентификации и характеристики их эффективности
Безусловно стойкие системы аутентификации
Вычислительно стойкие системы аутентификации
Пример практически используемой вычислительно стойкой системы аутентификации (режим выработки имитовставки для ГОСТ 28147)
Слайд 10Часть II. Криптосистемы с открытым ключом
Идея построения криптографии с открытым ключом
Математический базис КОК:
Основы теории чисел
Представление чисел в различных позиционных системах Битовые операции
Делимость. Алгоритм Евклида
Операции по числовому модулю (сравнения, конгруэнтность)
Возведение в степень
Вычисление дискретного логарифма
Малая теорема Ферма
Теорема Эйлера (обобщение теоремы Ферма)
Слайд 11Генерирование простых чисел
Важнейшие тесты по проверке простоты чисел
Построение криптосистем
Криптосистема РША (Райвеста–Шамирa–Адлемана)
( Метод формирования пар открытых/закрытых ключей для КС РША
Шифрование в КС РША, Дешифрование в КС РША)
Стойкость КС РША
Слайд 12
Метод распределения ключей Диффи–Хеллмана
КС Эль-Гамаля
Построение КС на
Элементы теории эллиптических кривых над конечными полями
Задание КС над эллиптическими кривыми
Обобщение КС Эль-Гамаля на случай эллиптических кривых
Построение системы распределения ключей Диффи– Хеллмана над эллиптическими кривыми
Слайд 13Цифровые подписи с использованием КС ОК
Основные требования, предъявляемые к ЦП
ЦП на основе КС РША
ЦП на основе КС Эль-Гамаля
Обобщение ЦП на случай эллиптических кривых
Бесключевые хеш-функции
Основные требования, предъявляемые к криптографическим ХФ
Способы построения стойких криптографических бесключевых ХФ
Выводы о возможности построения стойких ЦП
Слайд 14Основная литература по курсу
В.И.Коржик , В.П.Просихин , “Основы криптографии “,
Дополнительная литература по курсу
1.Б.Шнейер , “Прикладная криптография “, Триумф , 2002.
2.Menezes A.J.,et all “Handbook of applied cryptography”,CRC,1996.
3.Молдавян Н.А.. Молдавян А.А. .”Введение в криптосистемы с открытым
ключом”, БХВ, 2005.
4.Бабаш А.В.,Шанкин Г.П.. “История криптографии “, Гелиос , 2002.
5.Henk C.A. van Tilborg ,”Fundamentals of Cryptography”, Kluwer, 2001.
6.Болотов А.А. и др. “Элементарное введение в эллиптическую криптографию”,КомКнига, 2006
Слайд 15Перечень основных лабораторных работ по курсу (часть из них может не
Часть 1
1. Исследование идеальной системы шифрования
2.Криптоанализ блокового шифра тотальным перебором ключей
6. Основы теории конечных полей
7.Исследование блокового шифра AES.
8.Исследование свойств линейного рекуррентного регистра (ЛРР)
9.Криптоанализ потокового шифра на основе использования алгоритма Месси-Берлекэмпа
10.Криптоанализ потокового шифра на основе корреляционного метода
11.Исследование датчика шифрующей гаммы , реализованного основе ЛРР с управляемым тактированием
12.Исследование потокового шифра A5/1.
13.Исследование метода безусловно стойкой аутентификации сообщений
Слайд 16Часть 2
1.Основы теории чисел
2.Тестирование простых чисел и нахождение квадратичных вычетов
3.Исследование криптосистемы
4.Исследование криптосистемы с открытым ключом на основе эллиптических кривых
5.Исследование бесключевой хеш-функции , построенной по схеме Матиаса-Мейера-Осеаса
6.Исследование криптопротокола с разделением секретных данных между пользователями
7.Исследование протокола идентификации на основе концепции нулевых знаний.
Слайд 18В результате освоения дисциплины студент должен
знать:
основные математические методы и алгоритмы
основы электронной (цифровой) подписи в телекоммуникационных системах (ОК-1, ОК-9, ПК-1);
принципы работы, структурные схемы, протоколы и способы систем электронной подписи (ОК-1, ОК-2, ОК-5, ОК-6, ОК-9, ПК-17);;
уметь:
пользоваться методами теории чисел (ОК-1, ОК-9, ПК-1);
составлять протоколы шифрования и расшифрования сообщений (ОК-1, ОК-9, ПК-16, ПК-3);
рассчитывать основные характеристики и параметры криптографических алгоритмов защиты информации (ОК-1, ОК-9, ПК-1);
оценивать теоретическую и практическую стойкость шифров (ОК-9, ПК);
Слайд 19владеть:
приемами проектирования типовых алгоритмов криптозащиты и криптоанализа сообщений (ОК-1, ОК-9, ПК-18);
методами
навыками экспериментального исследования данных алгоритмов (ОК-9)
методами оценки криптостойкости систем защиты информации (ОК-9, ПК-17).
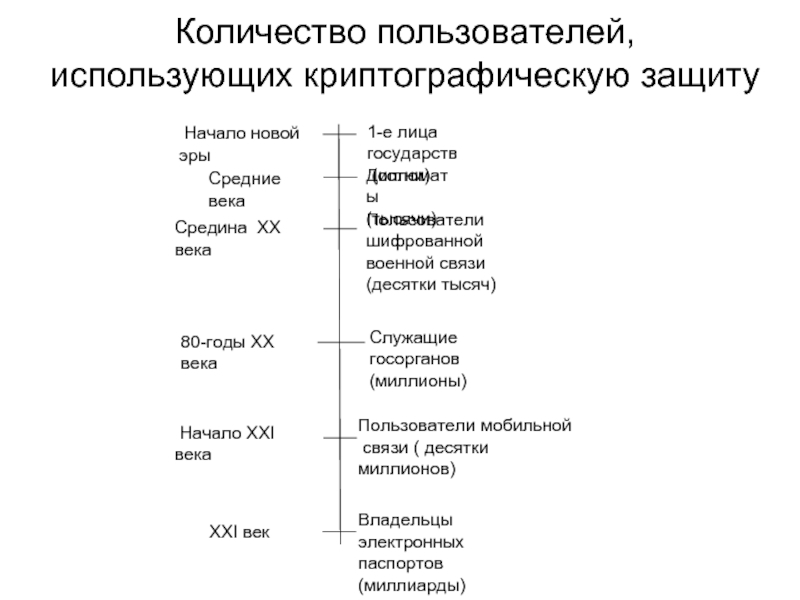
Слайд 202. Основные этапы исторического развития криптографии
17-й в. н.э. Шифр Виженера
1-й в.
1976 г. Криптография с открытым ключом
1977 г. Стандарт шифрования DES (США)
1948 г. Теория Шеннона
1926 г. Энигма
1917 г. Шифр Вернама
1994г. ГОСТ Р 34.10, Р 34.11
2001 г. ГОСТ Р 34.10
2000 г. Усиленный стандарт шифрования AES (США)
ГОСТ Р 34.11-2013, ГОСТ Р 34.10-2013
Слайд 24Шифр Виженера
Нумерация символов русского алфавита
Ei=Мi +Кi
Защита информации
ПриветПриветПривет
чсвлшу….
Слайд 25Основные виды криптографических преобразований
∙ Шифрование - сохранение тайны передаваемого сообщения;
∙
∙ Электронная цифровая подпись - подтверждение подлинности электронного документа и его авторства.
Слайд 27Описание модели шифрования
Описание источника
сообщений
SK=LN
En=E1,E2,….En
Описание источника криптограмм
{En}
SE=mn
{P(En)}
Слайд 29Основные уравнения системы шифрования
En=f(Mn,KNш)- уравнение шифрования
Mn=g(En,KNрш)- уравнение дешифрования
Слайд 30 Принцип Керхгоффа
Согласно этому принципу предполагается, что в данной модели
Основные типы криптографических атак:
1) только при известной криптограмме Е;
2) при известной криптограмме Е и соответствующей ей части сообщения M;
3) при специально выбранном сообщении M и соответствующей ему криптограмме E.
Слайд 31Типы криптосистем
По типу ключа криптосистемы делятся на симметричные (kш = kд = k) и
По способу формирования криптограммы из сообщения :
блоковые криптосистемы и потоковые криптосистемы.
Криптосистема называется блоковой, если каждый блок сообщения определенной длины шифруется по одному и тому же правилу; блок криптограммы имеет обычно ту же длину, что и блок сообщения (рис. 1.1).
Рис. 1.1. Блоковое шифрование
Слайд 34Стойкость систем шифрования
Стойкость - способность противостоять всевозможным атакам нарушителя, нацеленным на
Слайд 35Атаки нарушителя
1. Криптоанализ ведется, только на основе, перехваченных криптограмм;
2.Криптоанализ ведется на основе,
3.Криптоанализ ведется на основе выбираемого противником открытого сообщения;
Слайд 37Безусловно стойкие (идеальные) системы шифрования
Безусловно стойкой системой шифрования (БССШ) называется система
Лучшим способом дешифрования криптограммы БССШ является угадывание
одного из возможных сообщений источника Математически условие АССШ может
быть записано в виде.
.
- условная вероятность того, что сообщение Mi было зашифровано криптограммой Ej;
– априорная (при неизвестной криптограмме) вероятность присутствия сообщения Mi.
Слайд 38Эквивалентное определение БССШ
шенноновская информация в криптограмме Ej о сообщении Mi).
- энтропия
- энтропия источника сообщений
Слайд 40
Пример идеальной КС с гаммированием по mod 2
Пусть ,
– двоичные цепочки длины N. Криптограмма
где каждый бит сообщения складывается с каждым битом ключа по mod 2, имеет вид
Дешифрование :
.
.
.
Слайд 41Вычислительно стойкие системы шифрования
Система шифрования называется вычислительно стойкой (ВССШ),
если вскрытие такой
алгоритм вскрытия требует необозримо большого времени
или необозримо большой памяти устройств, с помощью которых
проводится криптоанализ
Время криптоанализа определяется:
1. Сложностью алгоритма дешифрования;
2. Быстродействием вычислительных устройств,
осуществляющих дешифрование
Слайд 42
Сложность алгоритмов криптоанализа должна соответствовать
сложности решения сложной задачи
Основные подходы к
Тотальный перебор ключей
Анализ статистических особенностей криптограмм
Линейный криптоанализ
Дифференциальный криптоанализ
Другие
Быстродействие вычислительных устройств 1010- 1012 операций/с
Быстродействие ЭВМ увеличивается в 4 раза каждые 3 года
Слайд 43Достаточное условие существования АССШ
Теорема 1. Система шифрования является абсолютно стойкой, если
М1
М2
Е1
Е2
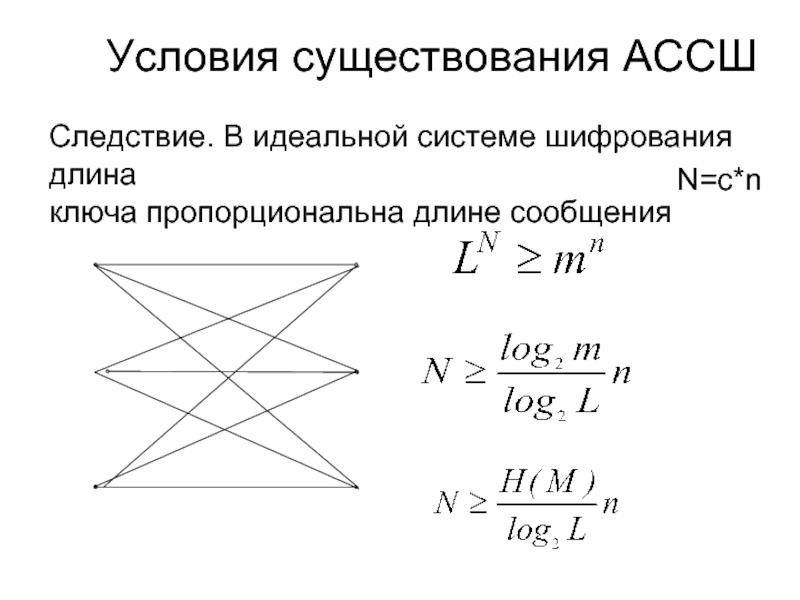
Слайд 44Условия существования АССШ
Следствие. В идеальной системе шифрования длина
ключа пропорциональна длине
N=c*n
Слайд 45Пример расчета длины ключа для БССШ
Параметра канала связи: V=10Мбит/с
Время передачи информации
Условия передачи - АССШ
Требуется найти длину ключа N.
Решение
Определим длину переданного сообщения за время 1сутки
N=1сутки*10Мбит/с=24*60*60*107=8,54*1011бит≈1011байт.
Если в качестве носителей ключа использовать CD емкостью
700Мбайт, то для обеспечения шифрованной связи (пересылки
и хранения ключа) необходимо расходовать 154 CD в сутки!.
КN
КN
Слайд 46Понятие расстояния единственности
Ключ (длина L)
Криптограмма (длина n)
Определение: Расстоянием единственности (РЕ)
называется
криптограммы, необходимое для однозначного восстановления
истинного ключа (сообщения) (без каких- либо ограничений на время его нахождения)
.
H(M)=
n*=NlogL/(logm-H(M))
lim H(Mn)/n – энтропия источника
n→∞
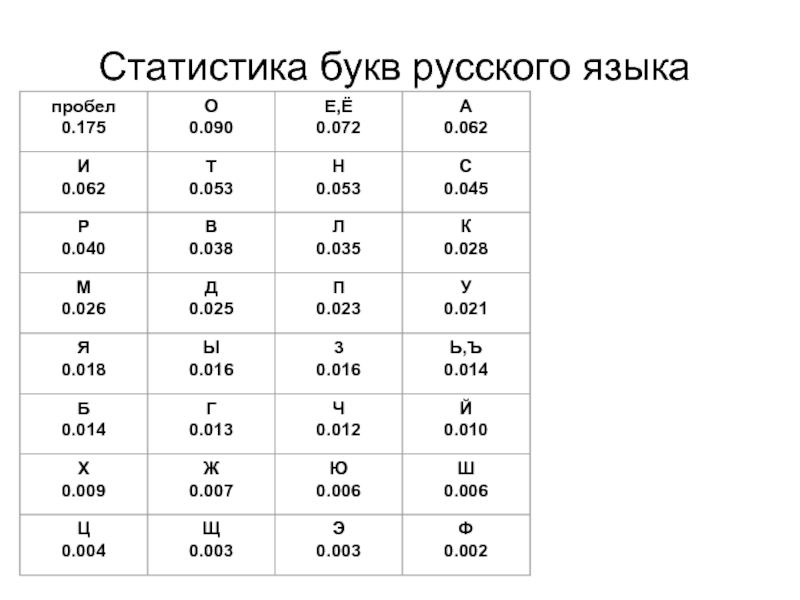
Слайд 47Пример расчета расстояния единственности
Для русского языка m=32
Энтропия H(M)=1,5-2,5 бит/символ
N=128,
Тогда расстояние единственности
n*=37-51 символ.







![Основные методы криптоанализа блоковых шифровЭлементы теории конечных полей [8, 9]Модификации блоковых шифров Многократное шифрованиеПримеры практически](/img/tmb/1/22712/bc341b493641a14ee8152548a771837a-800x.jpg)