- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сильноветвящиеся Б-деревья презентация
Содержание
- 1. Сильноветвящиеся Б-деревья
- 2. Если задать максимальное количество детей, то можно
- 3. Можно использовать список детей со ссылкой от
- 4. Алгоритмы, работающие с такими конструкциями, существенно зависят
- 5. Если не хватает оперативной памяти, то возможно
- 6. За одно обращение к диску считывается поддерево,
- 7.
- 8. Б-деревья порядка m
- 9.
- 10. Для каждой вершины (кроме корня) количество элементов
- 11.
- 12. Если на этой странице нет элементов, то
- 13.
- 14. Алгоритм построения Б-дерева порядка m Выполняется
- 15. К У Р А П О В
- 16. Эта схема сохраняет все характерные свойства Б-деревьев.
Слайд 1Сильноветвящиеся Б-деревья
Постановка задачи:
До сих пор рассматривались только двоичные деревья. Этого во
Если рассмотреть отношения «человек и его дети», то двоичных деревьев не всегда достаточно, требуются деревья со многими ветвями.
Будем называть их сильноветвящимися.
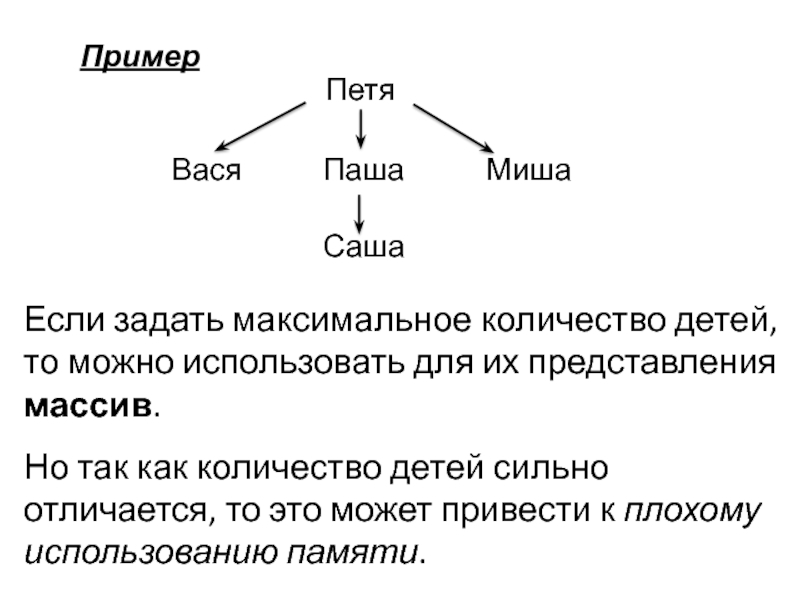
Слайд 2Если задать максимальное количество детей, то можно использовать для их представления
Но так как количество детей сильно отличается, то это может привести к плохому использованию памяти.
Пример
Слайд 3Можно использовать список детей со ссылкой от родителя на старшего ребенка.
Но
Например, при удалении Паши мы не можем поставить Сашу на его место.
Пример
Слайд 4Алгоритмы, работающие с такими конструкциями, существенно зависят от их описания.
Такая
В 70-е годы сильноветвящимся деревьям было найдено применение для следующей задачи:
Формирование и поддержание крупномасштабных деревьев поиска, в которых необходимо включение и добавление элементов, но для которых либо не хватает оперативной памяти, либо она слишком дорога для долговременного хранения.
Слайд 5Если не хватает оперативной памяти, то возможно использовать внешнюю память.
Решение:
Вершины дерева разместить во внешней памяти (на диске), а ссылки оставить в оперативной памяти и ссылаться на адреса на диске.
Т.к. работа с внешней памятью, то скорость обращения уменьшается и необходимо минимизировать количество обращений к диску.
Сильноветвящиеся деревья были идеальным решением, т.к. было предложено при одном обращении к диску считывать не одну вершину, а целую группу.
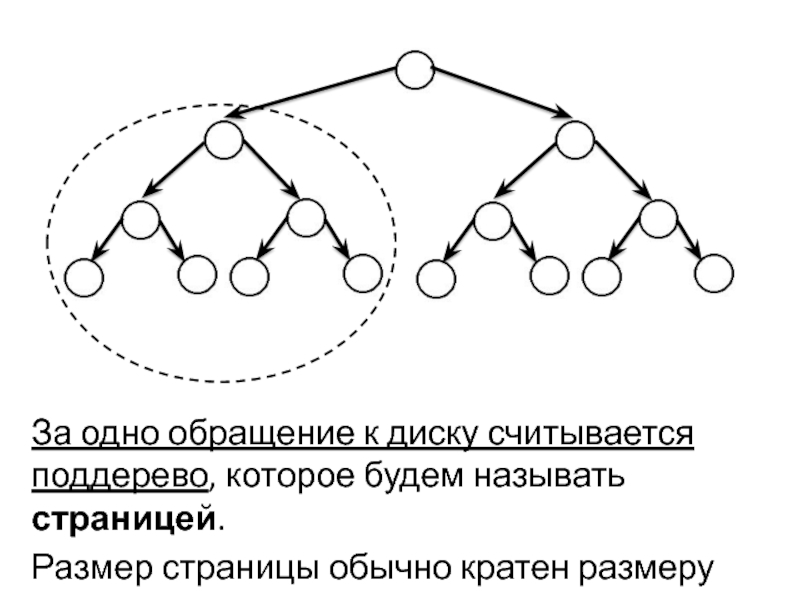
Слайд 6За одно обращение к диску считывается поддерево, которое будем называть страницей.
Размер
Слайд 10Для каждой вершины (кроме корня) количество элементов m ≤ k ≤
для корня 1 ≤ k ≤ 2m
3. Все листья дерева расположены на одном уровне (важное свойство).
Пример: Б-дерево порядка m=2
Root
• 10 • 20 •
• 5 • 8 •9 •
• 11 •14 •
• 21• 25 • 30•40 •
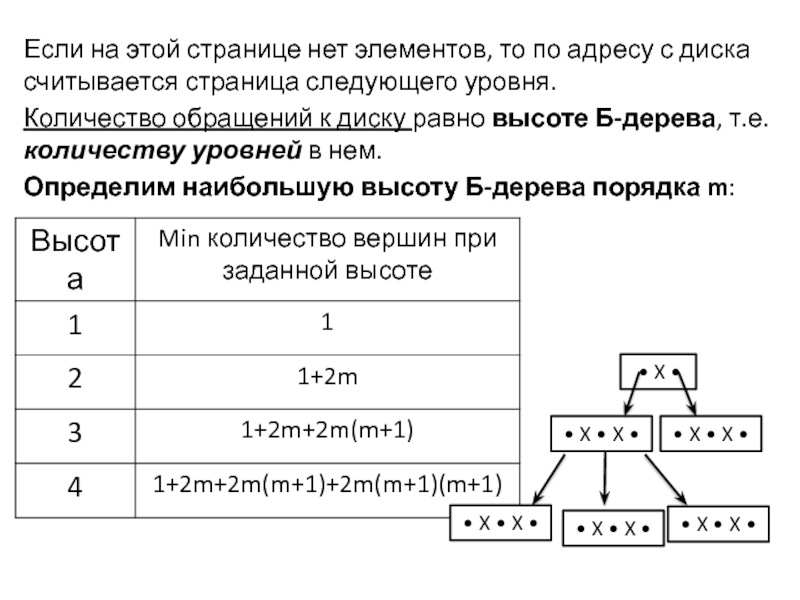
Слайд 12Если на этой странице нет элементов, то по адресу с диска
Количество обращений к диску равно высоте Б-дерева, т.е. количеству уровней в нем.
Определим наибольшую высоту Б-дерева порядка m:
• X •
• X • X •
• X • X •
• X • X •
• X • X •
• X • X •
Слайд 14Алгоритм построения Б-дерева порядка m
Выполняется поиск элемента D (добавляемые данные);
Если
Вставим элемент в позицию Р+1, количество элементов на странице увеличивается на 1;
Если k ≤ 2m, то процесс закончен (было место на странице);
Если k > 2m, то происходит переполнение страницы. Создаем новую страницу по адресу b?, на которую переносим m правых элементов, средний элемент переносим на родительскую страницу, m левых элементов оставляем на странице по адресу a?;
Включение элемента в родительскую страницу производится по тому же алгоритму;
Если родительской страницы нет, то она создается (корневая) с единственным элементом.
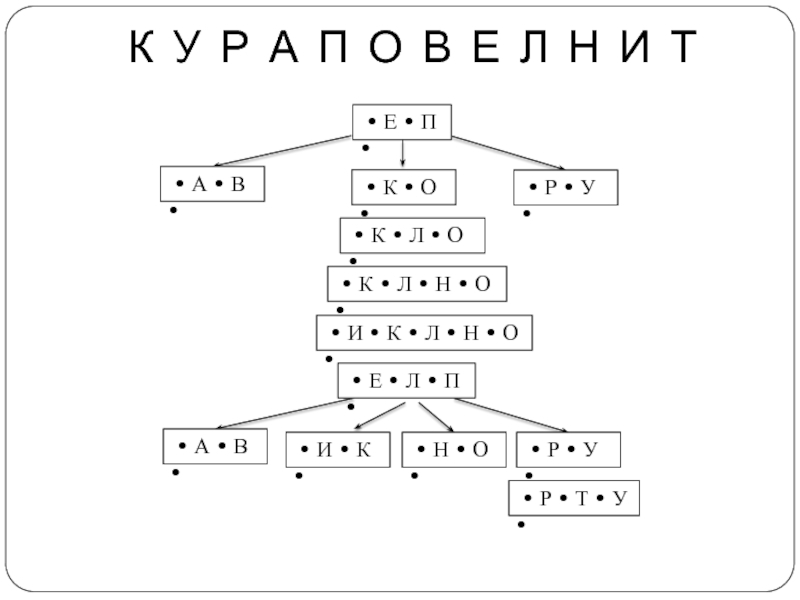
Слайд 15К У Р А П О В Е Л Н И
• К •
• К • У •
• К • Р • У •
• А • К • Р • У •
• А • К • П • Р • У •
• П •
• А • К •
• Р • У •
• П •
• А • К •
• Р • У •
• А • К • О •
• А • В • К • О •
• А • В • Е • К • О •
• Е • П •
• А • В •
• Р • У •
• К • О •
• Е • П •
• А • В •
• Р • У •
• К • О •
• К • Л • О •
• К • Л • Н • О •
• И • К • Л • Н • О •
• Е • Л • П •
• А • В •
• Р • У •
• И • К •
• Н • О •
• Р • Т • У •
Слайд 16Эта схема сохраняет все характерные свойства Б-деревьев.
Получившиеся две новых страницы содержат
Если включение элемента в родительскую страницу ведет к переполнению, то разделение страниц может распространиться до самого корня.
В этом случае может увеличиться высота дерева.
Таким образом, Б-деревья растут несколько странно: от листьев к корню.