к.т.н. Олег Романович Кивчун
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сигналы как элементы функциональных пространств (лекция № 6) презентация
Содержание
- 1. Сигналы как элементы функциональных пространств (лекция № 6)
- 2. 2 ЛЕКЦИЯ № 6 СИГНАЛЫ КАК
- 3. 3 Метрические и линейные пространства
- 4. 4 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 5. 5 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
- 6. 6 2. Пространства со скалярным произведением
- 7. 7 ВЕЩЕСТВЕННОЕ ЕВКЛИДОВО ПРОСТРАНСТВО
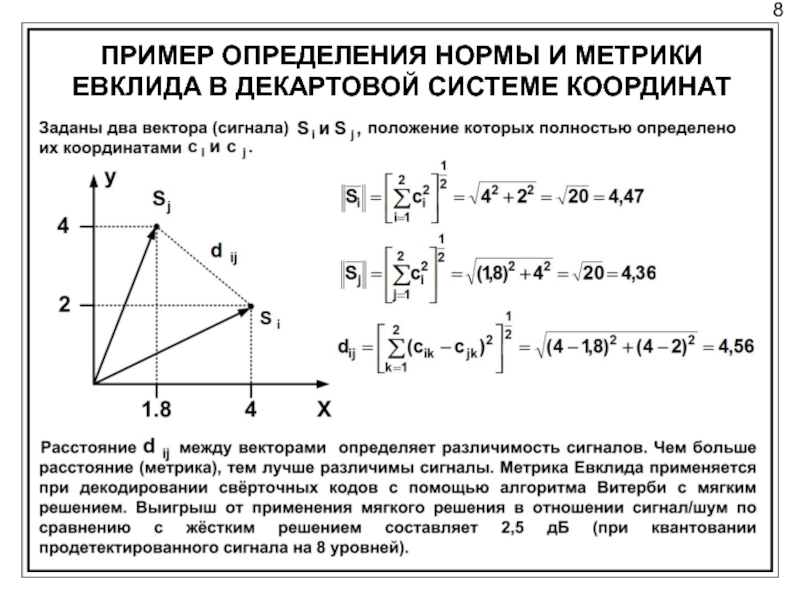
- 8. 8 ПРИМЕР ОПРЕДЕЛЕНИЯ НОРМЫ И МЕТРИКИ ЕВКЛИДА В ДЕКАРТОВОЙ СИСТЕМЕ КООРДИНАТ
- 9. 9 БЕСКОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО ГИЛЬБЕРТА И ХЕМИНГА
- 10. 10 ПРИМЕР ОПРЕДЕЛЕНИЯ НОРМЫ В ПРОСТРАНСТВЕ ХЕМИНГА
- 11. 11 3. Разложение сигналов в обобщённый ряд Фурье
- 12. 12 РАЗЛОЖЕНИЕ СИГНАЛОВ В РЯД ФУРЬЕ
- 13. 13 Таким образом, в результате изучения
- 14. 14 СПИСОК ЛИТЕРАТУРЫ Прокис Дж. Цифровая связь:
- 15. СПАСИБО ЗА ВНИМАНИЕ! 15
2 ЛЕКЦИЯ № 6 СИГНАЛЫ КАК ЭЛЕМЕНТЫ ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВ Метрические и линейные пространства. Пространства со скалярным произведением. Разложение сигналов в обобщённый ряд Фуре. СПИСОК ЛИТЕРАТУРЫ Основная: Теория электрической связи:
Слайд 1БАЛТИЙСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ имени И. КАНТА
1
Калининград
2012
РАЗДЕЛ I
ОБЩИЕ СВЕДЕНИЯ О СИСТЕМАХ
СВЯЗИ
Слайд 22
ЛЕКЦИЯ № 6
СИГНАЛЫ КАК ЭЛЕМЕНТЫ ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВ
Метрические и линейные пространства.
Пространства со
скалярным произведением.
Разложение сигналов в обобщённый ряд Фуре.
Разложение сигналов в обобщённый ряд Фуре.
СПИСОК ЛИТЕРАТУРЫ
Основная:
Теория электрической связи: Учеб. Для вузов / А.Г. Зюко, Д. Д. Кловский, В.И. Коржик, М. В. Назаров; Под ред. Д. Д. Кловского. – М.: Радио и связь, 1998. – 433 с.
Дополнительная:
Прокис Дж. Цифровая связь: Пер. с англ. / Под ред. Д.Д. Кловского. – М.: Радио и связь, 2000. – 800 с.
Бернард Скляр. Цифровая связь. Теоретические основы и практическое применение: Пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 1104 с.
Сухоруков А.С. Теория электрической связи: Конспект лекций. Часть 1. – М.:МТУСИ, ЦЕНТР ДО, 2002. – 65 с.
Сухоруков А.С. Теория цифровой связи: Учебное пособие. Часть 2. – М.:МТУСИ, 2008. – 53 с.
Слайд 1313
Таким образом, в результате
изучения лекции № 6 удалось сделать следующие
выводы:
сообщения, сигналы и помехи как векторы (точки) в линейном пространстве можно описать через набор координат в заданном базисе;
для ТЭС наибольший интерес при отображении сигналов представляет n-мерное пространство Евклида , бесконечное пространство Гильберта и дискретное пространство Хэмминга. В этих пространствах вводится понятие скалярного произведения двух векторов (x,y);
любую непрерывную функцию времени как элемент можно представить обобщенным рядом Фурье по заданному ортонормированному базису.
Слайд 1414
СПИСОК ЛИТЕРАТУРЫ
Прокис Дж. Цифровая связь: Пер. с англ. / Под ред.
Д.Д. Кловского. – М.: Радио и связь, 2000. – 800 с.
Бернард Скляр. Цифровая связь. Теоретические основы и практическое применение: Пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 1104 с.
Сухоруков А.С. Теория электрической связи: Конспект лекций. Часть 1. – М.:МТУСИ, ЦЕНТР ДО, 2002. – 65 с.
Сухоруков А.С. Теория цифровой связи: Учебное пособие. Часть 2. – М.:МТУСИ, 2008. – 53 с.
Аджемов А.С. Мир информационной реальности. – М.: ИРИАС, 2006. – 296 с.
Каганов В.И., Битюков В.К. Основы радиоэлектроники и связи: Учеб. пособие для вузов. – М.: Горячая линия-Телеком, 2007. – 542 с.
Стеценко О.А. Радиотехнические цепи и сигналы: Учебник. – М.: Высш. шк., 2007. – 432 с.
Санников В.Г. Сборник задач по курсу «Теория электрической связи»: Учеб. пособие. Часть 1. – М.: МТУСИ, 1992. – 62 с.
Санников В.Г. Сборник задач по курсу «Теория электрической связи»: Учеб. пособие. Часть 2. – М.: МТУСИ, 2001. – 65 с.
Санников В.Г. Дифференциальная импульсно-кодовая модуляция: Учеб. пособие. – М.: МТУСИ, 2006. – 56 с.
Бернард Скляр. Цифровая связь. Теоретические основы и практическое применение: Пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 1104 с.
Сухоруков А.С. Теория электрической связи: Конспект лекций. Часть 1. – М.:МТУСИ, ЦЕНТР ДО, 2002. – 65 с.
Сухоруков А.С. Теория цифровой связи: Учебное пособие. Часть 2. – М.:МТУСИ, 2008. – 53 с.
Аджемов А.С. Мир информационной реальности. – М.: ИРИАС, 2006. – 296 с.
Каганов В.И., Битюков В.К. Основы радиоэлектроники и связи: Учеб. пособие для вузов. – М.: Горячая линия-Телеком, 2007. – 542 с.
Стеценко О.А. Радиотехнические цепи и сигналы: Учебник. – М.: Высш. шк., 2007. – 432 с.
Санников В.Г. Сборник задач по курсу «Теория электрической связи»: Учеб. пособие. Часть 1. – М.: МТУСИ, 1992. – 62 с.
Санников В.Г. Сборник задач по курсу «Теория электрической связи»: Учеб. пособие. Часть 2. – М.: МТУСИ, 2001. – 65 с.
Санников В.Г. Дифференциальная импульсно-кодовая модуляция: Учеб. пособие. – М.: МТУСИ, 2006. – 56 с.
