- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Схемы программ (часть 1) презентация
Содержание
- 1. Схемы программ (часть 1)
- 2. Алгоритмы и машина Тьюринга Понятие алгоритма является
- 3. От алгоритма к программе Алгоритм как последовательность
- 4. От алгоритма к программе Переход от алгоритма
- 5. От программ к схемам программ Любое теоретическое
- 6. Операторный метод Начало теоретическому исследованию программ положили
- 7. Идея операторного метода Языки описания строения алгоритмов:
- 8. Идея операторного метода Поэтому базисные блоки в
- 9. Идея операторного метода Кроме того, вводятся дополнительные
- 10. Схемы Янова Идеи Ляпунова были развиты в
- 11. Схемы Янова
- 12. Продолжение работ Работу по эквивалентным преобразованиям операторных
- 13. Оптимизация и верификация программ Важность проблемы эквивалентных
- 14. Представления схем программ Схемы программ были введены
- 15. Текстовое представление схем программ Используемые для этого
- 16. Пример текстового представления схемы
- 17. Представление схем программ графами В графе, представляющем
- 18. Пример представления схемы в виде графа Ввод(x)
- 19. Интерпретация схемы Если на место каждого абстрактного
- 20. Назначение схем программ Схемы – это более
- 21. Классы схем программ Существуют различные классы схем
- 22. Характеризуются базисом и структурой схемы Базис класса
- 23. Полный базис В класса стандартных схем состоит
- 24. Х = {x, х1, х2..., у, у1
- 25. Р = {р(0), р(1), р(2)...; q(0), q(1),
- 26. Термами (функциональными выражениями) называются слова, построенные из
- 27. Тестами (логическими выражениями) называются логические константы и
- 28. Множество операторов включает пять типов: начальный оператор
- 29. условный оператор (тест) - логическое выражение; вхождения
- 30. Подклассы используют ограниченные базисы. Так, например, подкласс
- 31. Графы стандартных схем Для этой формы представления
- 32. Графы стандартных схем вершина-распознаватель, помеченная условным оператором;
- 33. Правильные схемы Переменная x∈ XS задана на
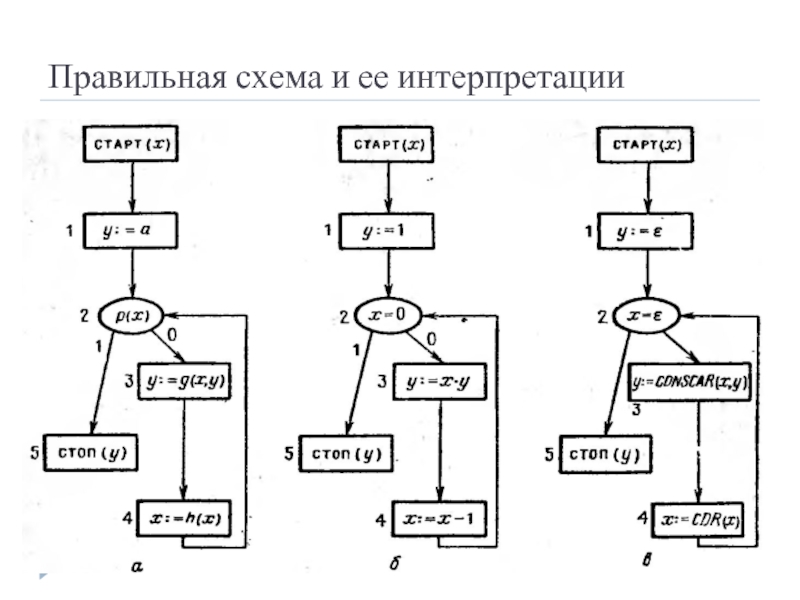
- 34. Правильная схема и ее интерпретации
- 35. Формальное определение интерпретации Интерпретацией базиса B в
- 36. Конечные интерпретации Определение интерпретации не уточняет природу
- 37. Стандартные программы Пара (S, I), где S
- 38. Примеры программ Базис: X = {x, y},
- 39. Память программы Памятью XS схемы S называется
- 40. Термами (функциональными выражениями) называются слова, построенные из
- 41. Тестами (логическими выражениями) называются логические константы и
- 42. Значения термов и тестов Значение терма τ
- 43. Конфигурация программы Конфигурацией программы (S,I) называется пара
Слайд 2Алгоритмы и машина Тьюринга
Понятие алгоритма является фундаментальным математическим понятием, которое не
Машина Тьюринга – это один из способов формализации понятия алгоритма, а точнее, понятия вычислимой функции
Тезис о возможности представления любого алгоритма эквивалентной машиной Тьюринга недоказуем именно в силу априорности понятия алгоритма
Слайд 3От алгоритма к программе
Алгоритм как последовательность «элементарных» операций над данными из
Такое представление называется программой. Пример – программа для машины Тьюринга
Слайд 4От алгоритма к программе
Переход от алгоритма к программе приводит к возникновению
проблема соответствия программы алгоритму ,
проблема однозначности программного представления алгоритма
Отсюда следует необходимость изучения программ как самостоятельных объектов
Слайд 5От программ к схемам программ
Любое теоретическое исследование начинается с построения модели
В случае программ такой теоретической моделью являются схемы программ
Схемы программ должны удовлетворять универсальным требованиям, предъявляемым к моделям:
игнорировать некоторые несущественные свойства, например, детали синтаксиса языка программирования;
воспроизводить все существенные для исследования свойства;
позволять изучать не отдельные программы, а их классы;
допускать возможность модификации и расширения
Слайд 6Операторный метод
Начало теоретическому исследованию программ положили работы отечественных учёных, относящиеся к
Он предложил операторный метод программирования, в котором впервые была предпринята формализация понятия программы и провозглашена, как фундаментальная, проблема разработки эквивалентных преобразований программ
Слайд 7Идея операторного метода
Языки описания строения алгоритмов: машины Тьюринга, продукции Поста, нормальные
Общий недостаток этих языков:
алгоритмы расчленяются на элементарные операции, что обусловливает огромные объемы описаний даже простейших реальных алгоритмов;
жесткий набор базисных элементарных операций не позволяет во всех случаях давать рациональное представление алгоритма
Слайд 8Идея операторного метода
Поэтому базисные блоки в описании должны быть достаточно крупными
Блоки должны связываться между собой логическими условиями, определяющими порядок выполнения блоков, обмен информацией и т.п.
Описание алгоритма через блоки и логические условия было названо Ляпуновым логической схемой алгоритма (схемой счета)
Блоки схемы счета Ляпунов называет операторами счета, а логические условия – распознавателями
Слайд 9Идея операторного метода
Кроме того, вводятся дополнительные блоки-операторы, получившие название операторов управления
Их назначение заключается в обеспечении нужной последовательности переходов в цепочке операторов счета и распознавателей
Пример логической схемы программы по Ляпунову:
x y z x A B y f z C t
1 2 2 1 2 3 3
Здесь A, B, C – операторы счета, x, y, z - переменные
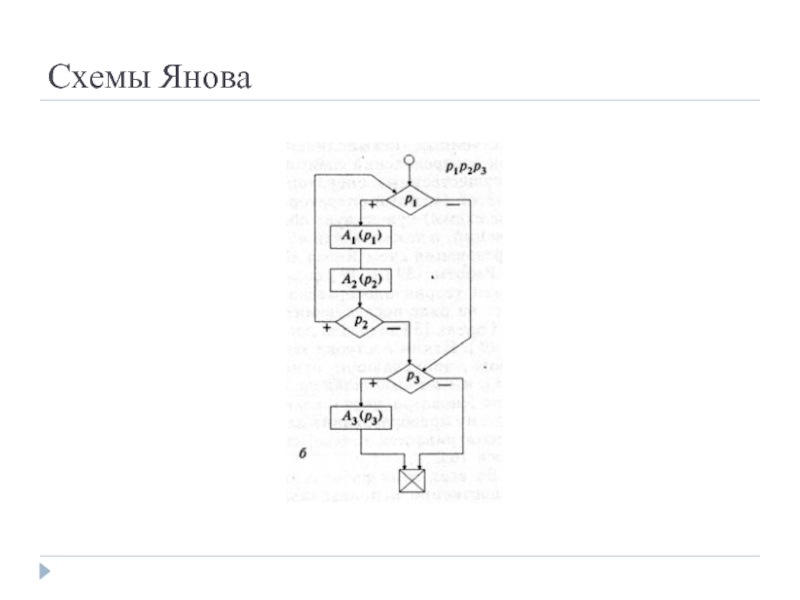
Слайд 10Схемы Янова
Идеи Ляпунова были развиты в работах его аспиранта Ю.И. Янова
В
дана формализация понятия схемы программы;
введено понятие эквивалентности схем;
предложен алгоритм, распознающий эквивалентность схем;
введена графовая форма представления схем
Слайд 12Продолжение работ
Работу по эквивалентным преобразованиям операторных схем программ продолжали и другие
Слушатели первого ляпуновского курса программирования А.П.Ершов, И.Б.Задыхайло, Э.З.Любимский, В.С.Штаркман участвовали в разработке первых в стране трансляторов, (программирующих программ)
Слайд 13Оптимизация и верификация программ
Важность проблемы эквивалентных преобразований вызвана потребностью улучшать те
Эта задача получила название проблемы оптимизации программ
Очень скоро к ней присоединилась проблема верификации программ, состоящая в проверке того, действительно ли программа реализует ту функцию, для вычисления которой она построена
Слайд 14Представления схем программ
Схемы программ были введены в качестве объектов, на которых
Схемы программ как и любая модель должны иметь какое-то представление
Для схем программ используются два основных представления – текстовое и графовое
Слайд 15Текстовое представление схем программ
Используемые для этого языки являются упрощенными копиями языков
Основное отличие текста программы от текста ее схемы состоит в следующем:
каждый оператор программы единственным образом задает некоторую вычислимую функцию над данными, а из этих отдельных функций образуется функция программы в целом;
в схемах индивидуальные операции и функции заменены абстрактными символами переменных-операций и переменных-предикатов
Слайд 17Представление схем программ графами
В графе, представляющем схему программы, вершины помечаются операторами
Представление схемы в виде графа является более наглядным, однако только при относительно малых своих объемах
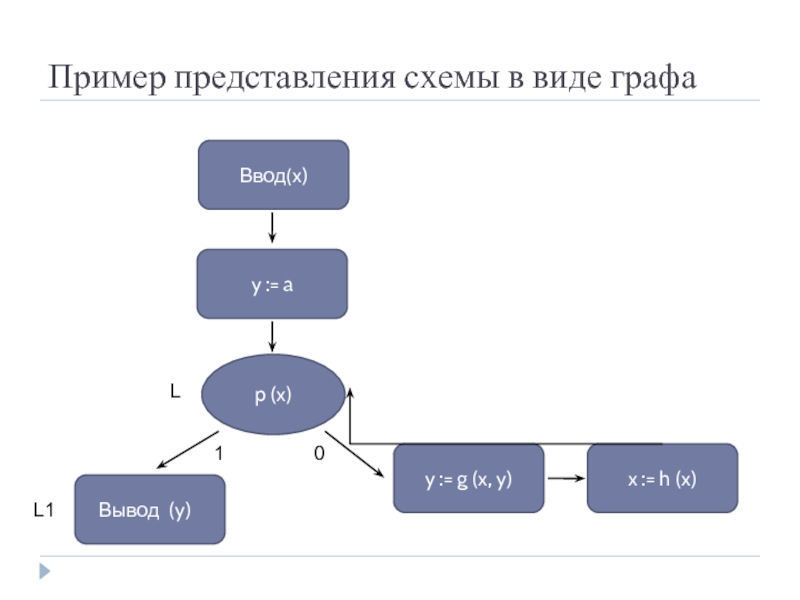
Слайд 18Пример представления схемы в виде графа
Ввод(x)
y := a
y := g (x,
x := h (x)
Вывод (y)
p (x)
L
L1
0
1
Слайд 19Интерпретация схемы
Если на место каждого абстрактного символа в схеме подставить соответствующую
Процесс такой подстановки называется интерпретацией схемы
Для одной и той же схемы могут быть предложены различные интерпретации и, соответственно, получены разные программы
Слайд 20Назначение схем программ
Схемы – это более простые объекты по сравнению с
Использование схем для анализа свойств программ делает этот анализ более простым
Результаты анализа схем носят более общий характер по сравнению с результатами анализа отдельных программ
Слайд 21Классы схем программ
Существуют различные классы схем программ, соответствующие либо различным классам
Для унификации описания различных схем вводится понятие класса стандартных схем, в качестве подклассов которого могут быть получены отдельные виды программных схем
Слайд 22Характеризуются базисом и структурой схемы
Базис класса стандартных схем:
фиксирует символы, из которых
указывает их роль (переменные, функциональные символы и др.),
задает вид выражений и операторов схем
Стандартные схемы программ
Слайд 23Полный базис В класса стандартных схем состоит из 4-х непересекающихся, счетных
Полный базис
Слайд 24Х = {x, х1, х2..., у, у1 у2..., z, z1, z2...}
F = {f(0), f(1), f(2)..., g(0), g(1), g(2)..., h(0), h(1), h(2)...} - множество функциональных символов; верхний символ задает местность символа; нульместные символы называют константами и обозначают начальными буквами латинского алфавита a, b, c...;
Множества символов полного базиса
Слайд 25Р = {р(0), р(1), р(2)...; q(0), q(1), q(2)...; } - множество
{start, stop, ..., := и т. д.} - множество специальных символов
Множества символов полного базиса
Слайд 26Термами (функциональными выражениями) называются слова, построенные из переменных, функциональных и специальных
односимвольные слова, состоящие из переменных или констант, являются термами;
слово τ вида f(n)(τ1, τ2, ..., τn), где τ1, τ2, ..., τn - термы, является термом;
те и только те слова, о которых говорится в п.п. 1,2, являются термами
Примеры термов: х, f(0), а, f(1)(х), g(2)(x, h(3)(y, a))
Термы
Слайд 27Тестами (логическими выражениями) называются логические константы и слова вида р(n)(τ1, τ2,...,
Примеры: p(0), p(0)(х), q(3)(x, y, z), p(2)(f(2)(x, y))
Допускается в функциональных и логических выражениях опускать индексы местности, если это не приводит к двусмысленности или противоречию.
Тесты
Слайд 28Множество операторов включает пять типов:
начальный оператор - слово вида start(х1, х2...хк),
заключительный оператор - слово вида stop(τ1, τ2,..., τn), где n ≥ 0, а τ1, τ2,..., τn - термы; вхождения переменных в термы τ называются аргументами этого оператора;
оператор присваивания - слово вида х := τ, где х – переменная (результат оператора), а τ - терм; вхождения переменных в термы называются аргументами этого оператора;
Операторы
Слайд 29условный оператор (тест) - логическое выражение; вхождения переменных в логическое выражение
оператор петли - односимвольное слово loop.
Среди операторов присваивания выделим случаи: когда τ - переменная, то оператор называется пересылкой (х:=у) и когда τ - константа, то оператор называется засылкой (х:=а).
Операторы
Слайд 30Подклассы используют ограниченные базисы. Так, например, подкласс V1 имеет базис: {х1,
Подклассы стандартных схем
Слайд 31Графы стандартных схем
Для этой формы представления стандартной схемой в базисе В
начальная вершина (единственная), помеченная начальным оператором; имеет одну выходящую дугу и не имеет входящих дуг;
заключительная вершина , помеченная заключительным оператором; не имеет выходящих дуг;
вершина преобразователь, помеченная оператором присваивания; имеет одну входящую дугу и одну выходящую;
Слайд 32Графы стандартных схем
вершина-распознаватель, помеченная условным оператором; имеет одну входящую дугу и
вершина-петля, помеченная оператором петли; не имеет выходящих дуг
Множество переменных, используемых в схеме S, составляет ее память XS
Для удобства дальнейших рассуждений будем снабжать вершины графа схемы именами, используя в качестве таковых целые числа
Начальная вершина имеет имя 0
Слайд 33Правильные схемы
Переменная x∈ XS задана на дуге e схемы S, если
Схема называется правильной, если на каждой ее дуге е заданы все переменные, которые являются аргументами оператора, помечающего конечную вершину этой дуги
Разметкой графа схемы называется процесс сопоставления каждой из его дуг множества заданных на ней переменных
Слайд 35Формальное определение интерпретации
Интерпретацией базиса B в области интерпретации D называется функция
каждой переменной x из базиса B – некоторый элемент d=I(x) из области интерпретации D;
каждой константе a из базиса B – некоторый элемент d=I(a) из области интерпретации D;
каждому функциональному символу f(n) (n≥1) – всюду определенную функцию F(n) = I(f(n)): D(n) → D;
каждой логической константе p(0) – один из символов множества {0,1};
каждому предикатному символу p(n) (n≥1) – всюду определенный предикат P(n) = I(p(n)): D(n) → {0,1};
Слайд 36Конечные интерпретации
Определение интерпретации не уточняет природу объектов области интерпретации (множества D
В частности это могут быть множества всех целых чисел, всех слов в некотором алфавите или подмножества этих множеств
Интерпретация I называется конечной, если ее область D – конечное множество
Слайд 37Стандартные программы
Пара (S, I), где S –схема в базисе B, а
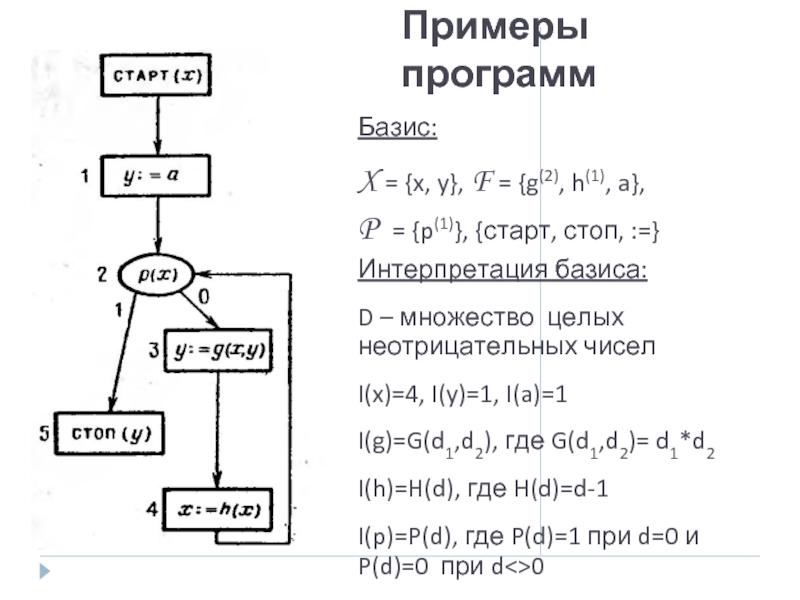
Слайд 38Примеры программ
Базис:
X = {x, y}, F = {g(2), h(1), a},
P
Интерпретация базиса:
D – множество целых неотрицательных чисел
I(x)=4, I(y)=1, I(a)=1
I(g)=G(d1,d2), где G(d1,d2)= d1*d2
I(h)=H(d), где H(d)=d-1
I(p)=P(d), где P(d)=1 при d=0 и P(d)=0 при d<>0
Слайд 39Память программы
Памятью XS схемы S называется конечное множество переменных, упоминаемых в
Состоянием памяти программы (S,I) называется функция W: XS → D, которая каждой переменной x из памяти схемы S сопоставляет элемент из области интерпретации D
Элемент W(x) называется значением переменной x в состоянии W
Слайд 40Термами (функциональными выражениями) называются слова, построенные из переменных, функциональных и специальных
односимвольные слова, состоящие из переменных или констант, являются термами;
слово τ вида f(n)(τ1, τ2, ..., τn), где τ1, τ2, ..., τn - термы, является термом;
те и только те слова, о которых говорится в п.п. 1,2, являются термами
Примеры термов: х, f(0), а, f(1)(х), g(2)(x, h(3)(y, a))
Термы
Слайд 41Тестами (логическими выражениями) называются логические константы и слова вида р(n)(τ1, τ2,...,
Примеры: p(0), p(0)(х), g(3)(x, y, z), p(2)(f(2)(x, y))
Допускается в функциональных и логических выражениях опускать индексы местности, если это не приводит к двусмысленности или противоречию.
Тесты
Слайд 42Значения термов и тестов
Значение терма τ при интерпретации I и состоянии
если τ = x , где x – переменная, то τI (W ) = W (x);
если τ = a, где a – константа, то τI (W ) = I (a);
если τ = f(n) (τ1, τ2, . . . , τn), то τI (W ) = I (f(n) ) (τ1I (W ) , τ2I (W ) , . . . , τnI (W ) );
Аналогично определяется значение теста π при интерпретации I и состоянии памяти W (обозначение: πI (W ) ): если π = p(n)(τ1, τ2, . . . , τn), n≥0, то
πI (W ) = I (p(n) ) (τ1I (W ) , τ2I (W ) , . . . , τnI (W ) );
Слайд 43Конфигурация программы
Конфигурацией программы (S,I) называется пара u=(k,W), где k – метка
Выполнение программы описывается конечной или бесконечной последовательностью конфигураций, которая называется протоколом выполнения программы