- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение уравнений с использованием ЭВМ презентация
Содержание
Слайд 2«Численные
методы решения нелинейных уравнений на
ЭВМ».
Задача отыскания корней нелинейного
уравнения вида f (x)
= 0 , где f (x) — непрерыв-
ная на отрезке [a,b] функция, не теряет акту-
альности и в наши дни, хотя имеет многове-
ковую историю. Она может быть использована
при решении уравнений, которые возникают
в математике, физике, технике и т. д. Суще-
ствует много методов, позволяющих достаточно
быстро находить приближённое значение корня
с требуемой точностью. В этой разработке рас-
сматривают метод деления отрезка пополам
(дихотомии) и метод Ньютона (касательных)
в программе Microsoft Excel, системах програм-
мирования TurboPascal, VB5.0 CCE, математи-
ческой системе автоматического проектирова-
ния Mathcad.
ная на отрезке [a,b] функция, не теряет акту-
альности и в наши дни, хотя имеет многове-
ковую историю. Она может быть использована
при решении уравнений, которые возникают
в математике, физике, технике и т. д. Суще-
ствует много методов, позволяющих достаточно
быстро находить приближённое значение корня
с требуемой точностью. В этой разработке рас-
сматривают метод деления отрезка пополам
(дихотомии) и метод Ньютона (касательных)
в программе Microsoft Excel, системах програм-
мирования TurboPascal, VB5.0 CCE, математи-
ческой системе автоматического проектирова-
ния Mathcad.
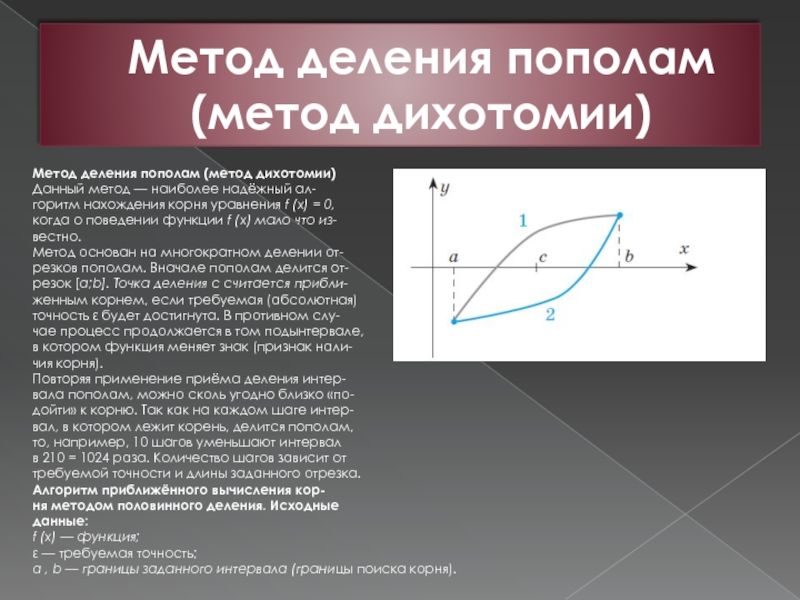
Слайд 3Метод деления пополам (метод дихотомии)
Метод деления пополам (метод дихотомии)
Данный метод —
наиболее надёжный ал-
горитм нахождения корня уравнения f (x) = 0,
когда о поведении функции f (x) мало что из-
вестно.
Метод основан на многократном делении от-
резков пополам. Вначале пополам делится от-
резок [a;b]. Точка деления c считается прибли-
женным корнем, если требуемая (абсолютная)
точность ε будет достигнута. В противном слу-
чае процесс продолжается в том подынтервале,
в котором функция меняет знак (признак нали-
чия корня).
Повторяя применение приёма деления интер-
вала пополам, можно сколь угодно близко «по-
дойти» к корню. Так как на каждом шаге интер-
вал, в котором лежит корень, делится пополам,
то, например, 10 шагов уменьшают интервал
в 210 = 1024 раза. Количество шагов зависит от
требуемой точности и длины заданного отрезка.
Алгоритм приближённого вычисления кор-
ня методом половинного деления. Исходные
данные:
f (x) — функция;
ε — требуемая точность;
a , b — границы заданного интервала (границы поиска корня).
горитм нахождения корня уравнения f (x) = 0,
когда о поведении функции f (x) мало что из-
вестно.
Метод основан на многократном делении от-
резков пополам. Вначале пополам делится от-
резок [a;b]. Точка деления c считается прибли-
женным корнем, если требуемая (абсолютная)
точность ε будет достигнута. В противном слу-
чае процесс продолжается в том подынтервале,
в котором функция меняет знак (признак нали-
чия корня).
Повторяя применение приёма деления интер-
вала пополам, можно сколь угодно близко «по-
дойти» к корню. Так как на каждом шаге интер-
вал, в котором лежит корень, делится пополам,
то, например, 10 шагов уменьшают интервал
в 210 = 1024 раза. Количество шагов зависит от
требуемой точности и длины заданного отрезка.
Алгоритм приближённого вычисления кор-
ня методом половинного деления. Исходные
данные:
f (x) — функция;
ε — требуемая точность;
a , b — границы заданного интервала (границы поиска корня).