- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение инженерных задач на ЭВМ. Лекция 4 презентация
Содержание
- 1. Решение инженерных задач на ЭВМ. Лекция 4
- 2. ФОРМУЛИРОВКА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- 3. т.е. при
- 4. СТАЦИОНАРНЫЕ КРАЕВЫЕ ЗАДАЧИ Рассмотрим некоторую двумерную
- 5. Искомая функция U = U(x,y) внутри области
- 7. Первая краевая задача (Дирихле) Пусть задана прямоугольная
- 8. Вторая краевая задача (Неймана) Пусть задана
- 9. Третья краевая задача (смешанная) На контуре
- 10. Собственно - смешанная краевая задача Краевые условия
- 11. К собственно – смешанным задачам относятся контактные
- 12. Однако точные методы применимы в основном к
- 13. Решение инженерных задач на
- 14. Среди них чаще всего применяют разностные методы,
- 15. 1. Для применения этого разностного метода в
- 16. Требуется найти функцию U(x,y) внутри некоторой
- 17. Рассмотрим частный случай квадратной ячейки h =
- 18. Граничный узел 2-го рода – не
- 19. x y Gk Гh h h
- 20. Рассмотрим внутренний узел области G.
- 21. Для каждой внутренней точки области G, т.е.
- 22. 3. Получим СЛАУ (5.5) – (5.6) относительно
- 23. Самостоятельно: Записать преобразованные с помощью конечно-разностных выражений:
- 24. x y h=1
- 25. x h=1 h=1 a =6 b=4
- 26. x
Слайд 2ФОРМУЛИРОВКА КРАЕВЫХ ЗАДАЧ ДЛЯ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
В этих КЗ обязательно заданы
Динамические КЗ формулируются для уравнений гиперболического и параболического типов.
Краевые задачи для уравнений математической физики подразделяются на
ДИНАМИЧЕСКИЕ
СТАЦИОНАРНЫЕ
Слайд 3
т.е. при U ≡ 0
Например, для КЗ колебания растянутой струны условие будет записано так:
U t = 0 = f(x);
U ×= 0 = 0 ; U × = l = 0
t = 0= F(x)
(4.1)
Если рассматривать колебания бесконечно длинной струны, то краевые условия выполняются автоматически,
U t = 0 = f(x);
t = 0= F(x)
(4.2)
начальные условия
краевые условия
начальные условия
Слайд 4СТАЦИОНАРНЫЕ КРАЕВЫЕ ЗАДАЧИ
Рассмотрим некоторую двумерную область G с граничным
Покажем на примере уравнения Лапласа формулировку всех КЗ для двумерной области (для других областей – формулировка аналогична).
формулируются для эллиптических уравнений
В зависимости от вида краевых условий стационарные КЗ подразделяются на 3 класса.
x
y
G
Г
Слайд 5Искомая функция U = U(x,y) внутри области G удовлетворяет ДУ Лапласа,
U Г = f(x,y)
Первая краевая задача (Дирихле)
(4.3)
Вторая краевая задача (Неймана)
Искомая функция U = U(x,y) внутри области G удовлетворяет ДУ Лапласа, а на контуре Г нормальная производная совпадает с заданной функцией φ(x,y)
Г = φ (x,y)
(4.4)
краевое условие Дирихле
краевое условие Неймана
n
n
Слайд 6
Искомая функция U = U(x,y) внутри области G удовлетворяет ДУ
(αU + ) Г = ψ (x,y)
3. Третья краевая задача (смешанная)
(4.5)
Покажем на примере формулировку трех типов краевых задач.
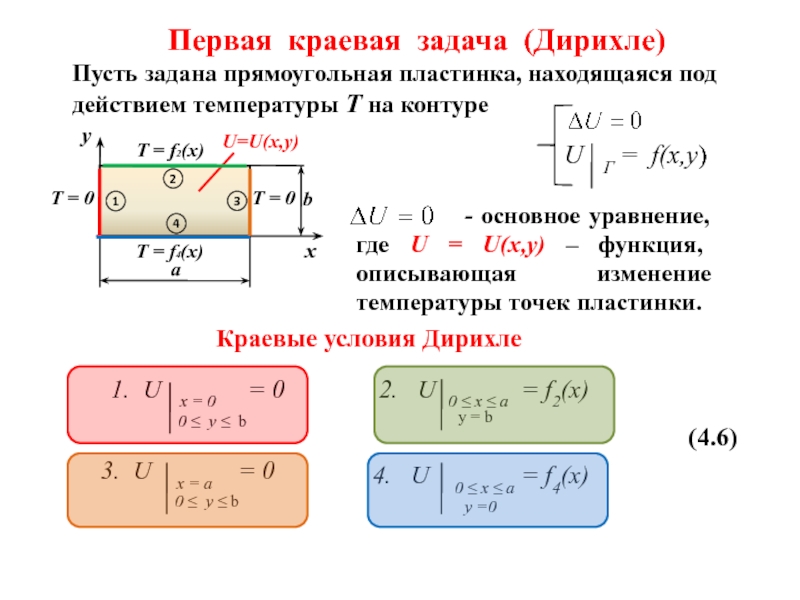
Слайд 7Первая краевая задача (Дирихле)
Пусть задана прямоугольная пластинка, находящаяся под действием температуры
U Г = f(x,y)
- основное уравнение, где U = U(x,y) – функция, описывающая изменение температуры точек пластинки.
x
y
a
b
T = f4(x)
T = 0
T = f2(x)
T = 0
4
1
2
3
U=U(x,y)
Краевые условия Дирихле
3. U x = a = 0
1. U x = 0 = 0
2. U 0 ≤ x ≤ a = f2(x)
(4.6)
0 ≤ y ≤ b
y = b
4. U 0 ≤ x ≤ a = f4(x)
y =0
0 ≤ y ≤ b
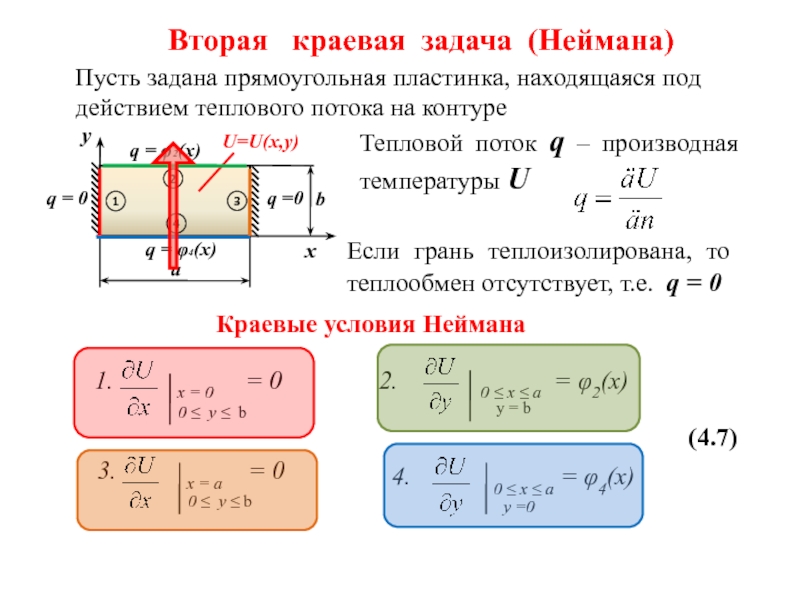
Слайд 8Вторая краевая задача (Неймана)
Пусть задана прямоугольная пластинка, находящаяся под действием
x
y
a
b
q = φ4(x)
q = 0
q = φ2(x)
q =0
4
1
2
3
U=U(x,y)
Краевые условия Неймана
3. x = a = 0
1. x = 0 = 0
2. 0 ≤ x ≤ a = φ2(x)
(4.7)
0 ≤ y ≤ b
y = b
4. 0 ≤ x ≤ a = φ4(x)
y =0
0 ≤ y ≤ b
Тепловой поток q – производная температуры U
Если грань теплоизолирована, то теплообмен отсутствует, т.е. q = 0
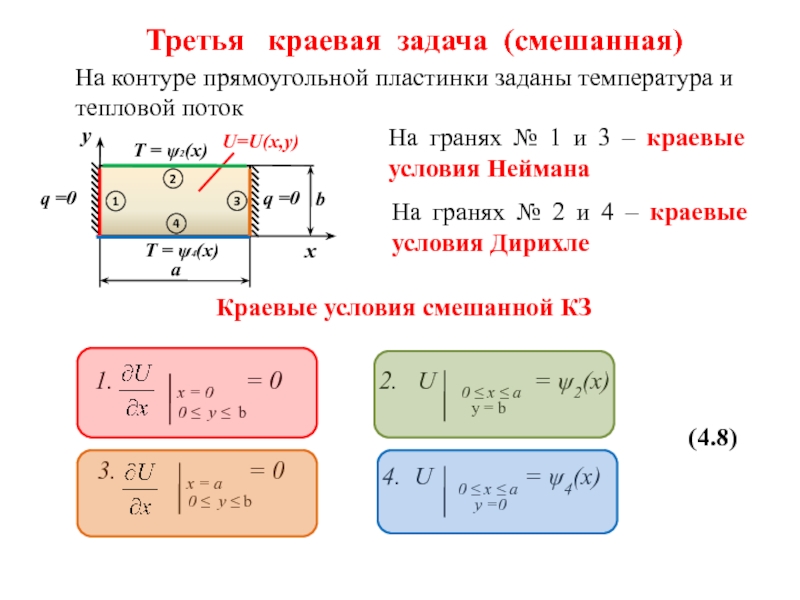
Слайд 9Третья краевая задача (смешанная)
На контуре прямоугольной пластинки заданы температура и
x
y
a
b
Т = ψ4(x)
q =0
Т = ψ2(x)
q =0
4
1
2
3
U=U(x,y)
Краевые условия смешанной КЗ
3. x = a = 0
1. x = 0 = 0
2. U 0 ≤ x ≤ a = ψ2(x)
(4.8)
0 ≤ y ≤ b
y = b
4. U 0 ≤ x ≤ a = ψ4(x)
y =0
0 ≤ y ≤ b
На гранях № 1 и 3 – краевые условия Неймана
На гранях № 2 и 4 – краевые условия Дирихле
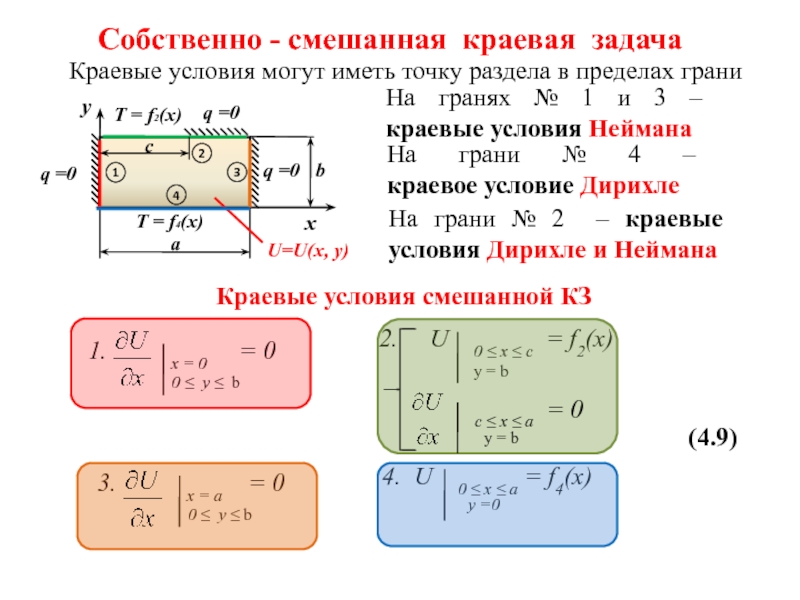
Слайд 10Собственно - смешанная краевая задача
Краевые условия могут иметь точку раздела в
x
y
a
b
Т = f4(x)
q =0
Т = f2(x)
q =0
4
1
2
3
U=U(x, y)
Краевые условия смешанной КЗ
3. x = a = 0
1. x = 0 = 0
2. U 0 ≤ x ≤ c = f2(x)
(4.9)
0 ≤ y ≤ b
y = b
4. U 0 ≤ x ≤ a = f4(x)
y =0
0 ≤ y ≤ b
На гранях № 1 и 3 – краевые условия Неймана
На грани № 4 – краевое условие Дирихле
q =0
c
На грани № 2 – краевые условия Дирихле и Неймана
с ≤ x ≤ а = 0
y = b
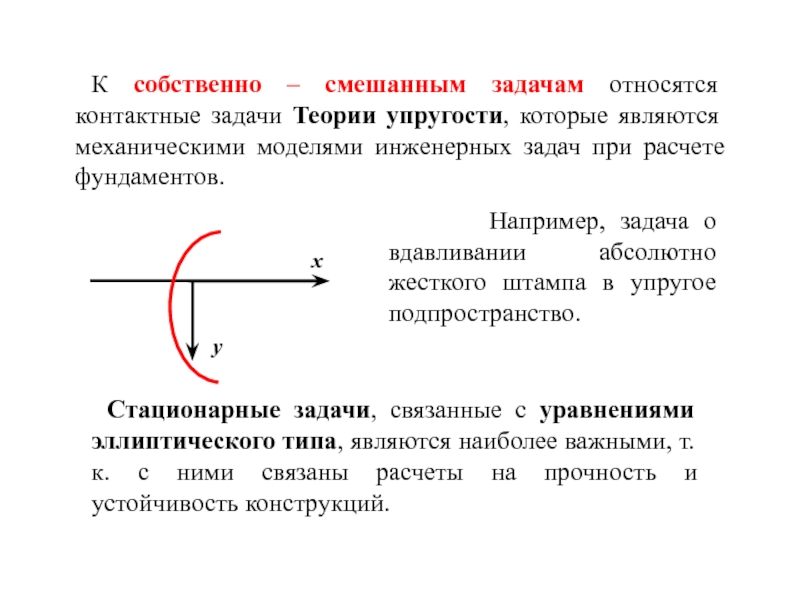
Слайд 11К собственно – смешанным задачам относятся контактные задачи Теории упругости, которые
Стационарные задачи, связанные с уравнениями эллиптического типа, являются наиболее важными, т.к. с ними связаны расчеты на прочность и устойчивость конструкций.
Например, задача о вдавливании абсолютно жесткого штампа в упругое подпространство.
x
y
Слайд 12Однако точные методы применимы в основном к линейным задачам в областях
ЧИСЛЕННЫЕ МЕТОДЫ ДЛЯ РЕШЕНИЯ
ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Для многочисленных задач МФ не существует универсального метода, пригодного для всех задач.
В курсах уравнений МФ изложен ряд методов, позволяющих для некоторых классов задач найти точное решение: метод распространяющихся волн, метод разделения переменных, метод функций источника и др.
Слайд 14Среди них чаще всего применяют разностные методы, благодаря их универсальности и
Задачи для нелинейных уравнений с коэффициентами достаточно общего вида
Задачи для линейных уравнений, но в областях сложной формы
редко удается решить классическими методами.
Основным способом решения таких задач являются ЧИСЛЕННЫЕ МЕТОДЫ
МЕТОД СЕТОК – обобщение Метода конечных разностей для случая многих неизвестных.
Слайд 151. Для применения этого разностного метода в области изменения функции U(x,y)
МЕТОД СЕТОК
4. Решая полученную алгебраическую систему, находят приближенное (разностное) решение в узлах сетки
3. Получающиеся при этом алгебраические уравнения называют разностной схемой.
2. Все производные, входящие в ДУ и краевые условия, заменяют разностями значений функции U(x,y) в узлах сетки.
АЛГОРИТМ РЕАЛИЗАЦИИ МЕТОДА
Слайд 16Требуется найти функцию U(x,y) внутри некоторой области G
U Г = ψ(x,y)
Рассмотрим применение метода сеток для решения краевой задачи Дирихле в случае уравнения Пуассона (плоский случай).
(5.1)
(5.2)
x
y
G
Г
Предполагается, что среда сплошная и искомое решение U = U(x,y) не имеет особенностей.
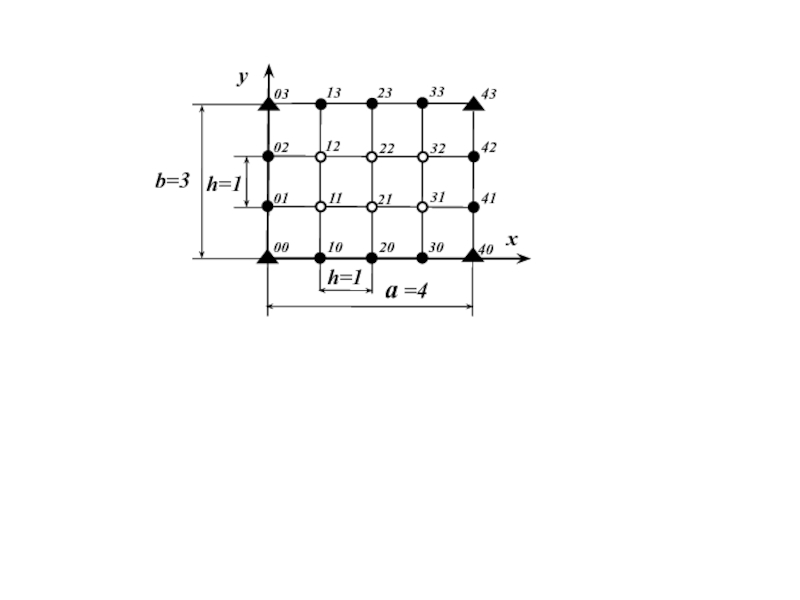
Слайд 17Рассмотрим частный случай квадратной ячейки h = l.
xi = x0
1. В плоской области G строится сеточная область GК , состоящая из одинаковых прямоугольных ячеек и приближающая данную область.
x
y
G
Г
ИДЕЯ МЕТОДА СЕТОК
Сетка строится путем проведения системы равноотстоящих линий
yk = y0 +k ∙l, k = 0, 1, …, m
Конфигурацию узлов называют шаблоном.
Шаблон может прямоугольным, квадратным, треугольным.
Узлы сетки принадлежат области G или отстоят на расстояние, не превышающее h.
От выбора основного размера ячеек зависит точность решения.
Слайд 18
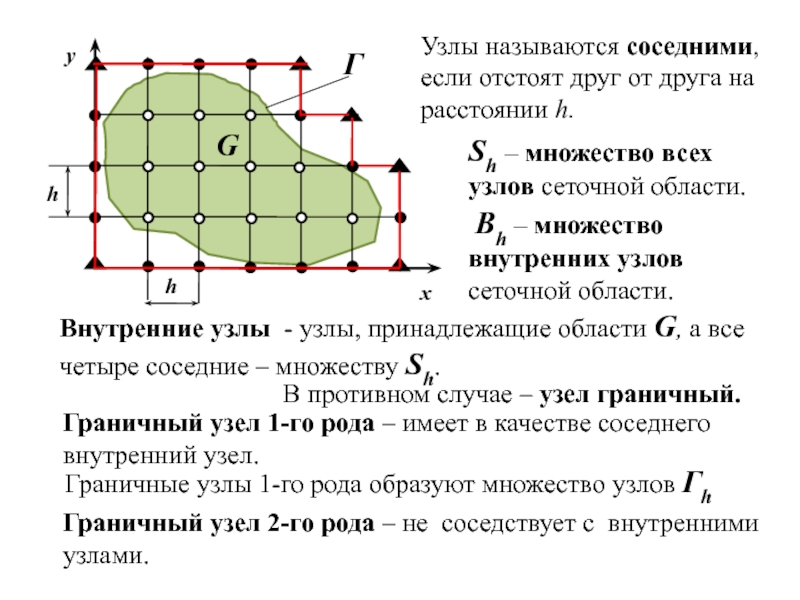
Граничный узел 2-го рода – не соседствует с внутренними узлами.
Вh
Узлы называются соседними, если отстоят друг от друга на расстоянии h.
x
y
G
Г
Sh – множество всех узлов сеточной области.
Внутренние узлы - узлы, принадлежащие области G, а все четыре соседние – множеству Sh.
В противном случае – узел граничный.
Граничный узел 1-го рода – имеет в качестве соседнего внутренний узел.
Граничные узлы 1-го рода образуют множество узлов Гh
h
h
Слайд 19x
y
Gk
Гh
h
h
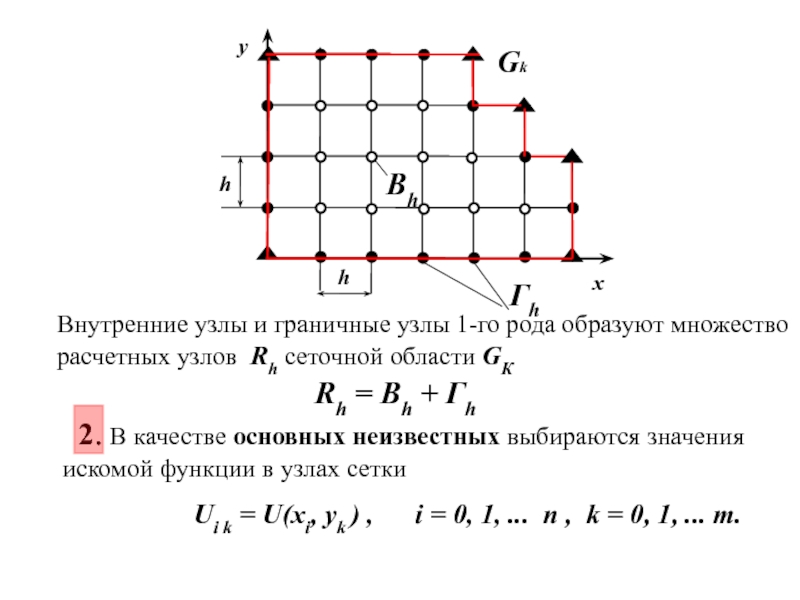
Внутренние узлы и граничные узлы 1-го рода образуют множество расчетных узлов
Rh = Вh + Гh
Вh
2. В качестве основных неизвестных выбираются значения искомой функции в узлах сетки
Ui k = U(xi, yk ) , i = 0, 1, ... n , k = 0, 1, ... m.
Слайд 20Рассмотрим внутренний узел области G.
i, k
i -1, k
i+1, k
i, k-1
i,
В каждом узле можно использовать конечно-разностные уравнения, обобщив их на случай частных производных
(5.3)
(5.4)
Слайд 21Для каждой внутренней точки области G, т.е. для каждого внутреннего узла
Для уравнения Пуассона ΔU = f(x , y) или
где fi , k = f(xi , yk ), i = 1, … n -1 , k = 1, ... m -1.
(5.5)
На основании краевых условий (5.2) устанавливаются значения искомого решения в граничных узлах области GК.
В граничных узлах 1-го рода
U (Гh ) = ψ (С ),
где С – ближайшая к Гh точка контура Г области G.
(5.6)
Слайд 223. Получим СЛАУ (5.5) – (5.6) относительно неизвестных Ui k
Количество уравнений
Rh = Вh + Гh
Количество неизвестных СЛАУ равно числу расчетных узлов Rh сеточной области GК (внутренние узлы + граничные узлы 1-го рода)
Система уравнений (5.5) и (5.6) всегда совместна, когда речь идет о решении задачи Дирихле.
Лишние неизвестные (Гh ) в системе (5.5) исключаются с помощью краевых условий (5.6).
4. Решив полученную систему уравнений, определяем приближенные значения искомой функции в узлах сеточной области GК.
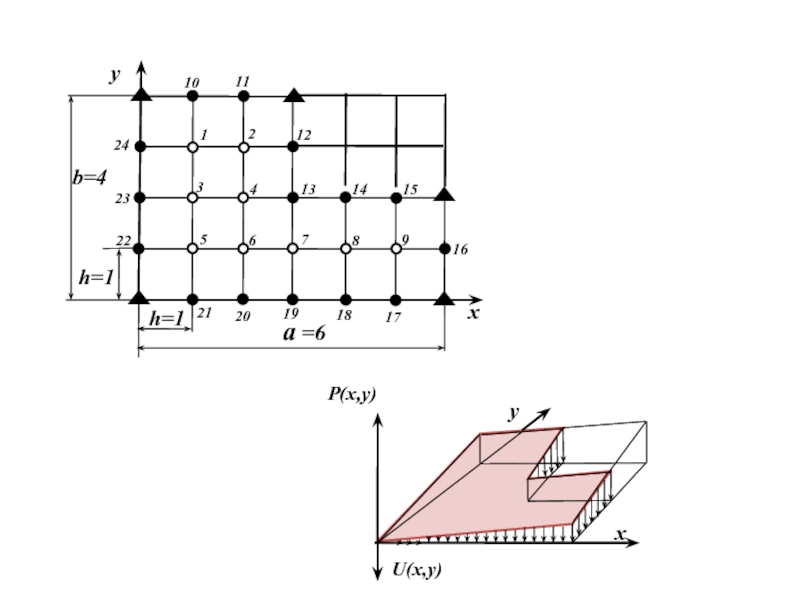
Слайд 23Самостоятельно:
Записать преобразованные с помощью конечно-разностных выражений:
для сетки с прямоугольной (l = h) и квадратной (l = h) ячейкой.