4 семестр
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Рекурсия. Состояние стека и дерево рекурсии при вычислении чисел Фибоначчи презентация
Содержание
- 1. Рекурсия. Состояние стека и дерево рекурсии при вычислении чисел Фибоначчи
- 2. Объект называется рекурсивным, если он содержит сам себя или определен с помощью самого себя
- 5. Состояние стека и дерево рекурсии при вычислении
- 6. Применение принципа «Разделяй и властвуй» для поиска
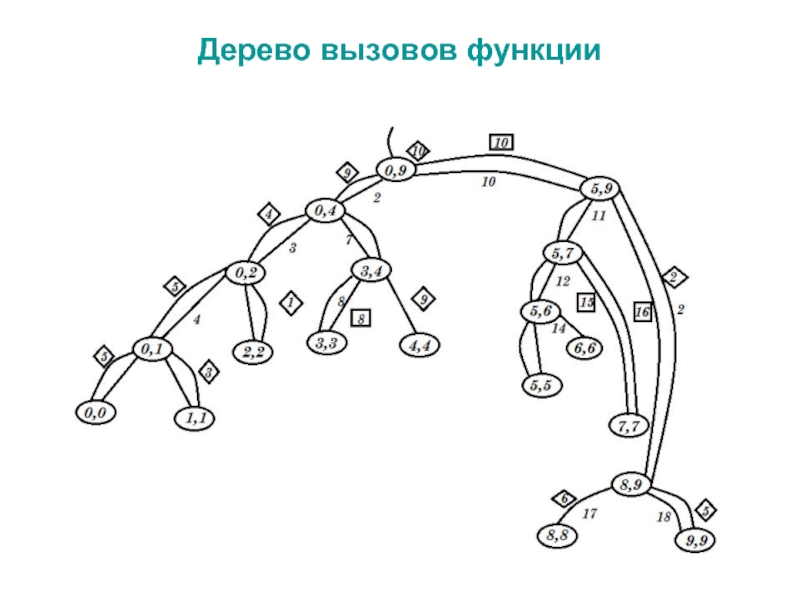
- 7. Дерево вызовов функции
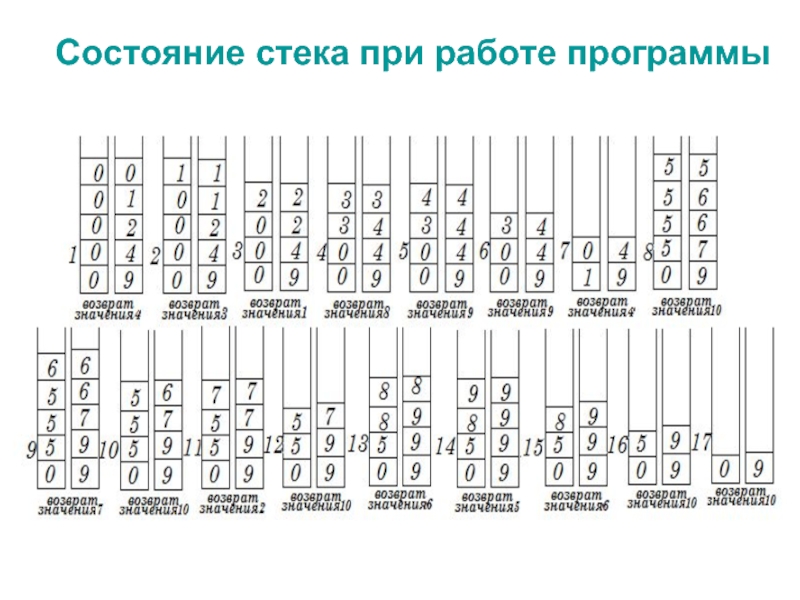
- 8. Состояние стека при работе программы
- 9. Ханойские башни
- 10. Стержни: А – исходный, С – целевой,
- 11. Программная реализация void main() { . .
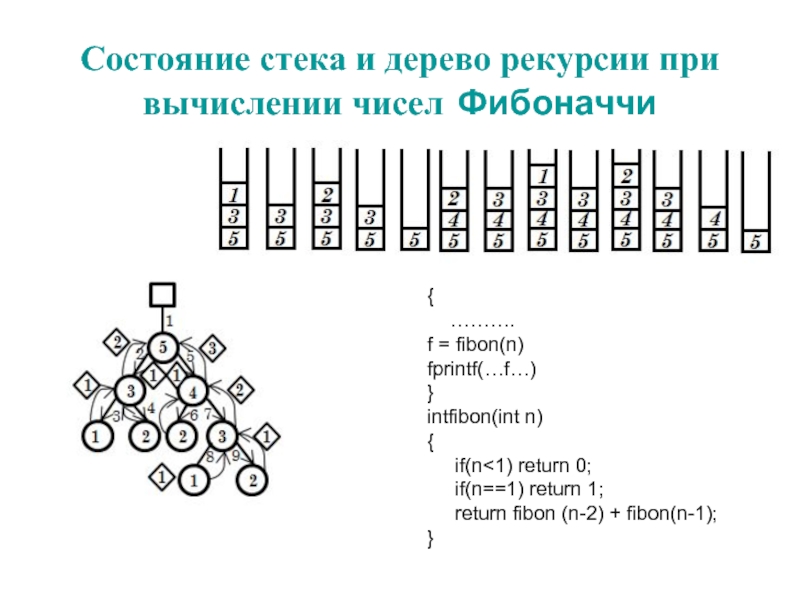
Слайд 5Состояние стека и дерево рекурсии при вычислении чисел Фибоначчи
{
……….
f = fibon(n)
fprintf(…f…)
}
intfibon(int n)
{
if(n<1) return 0;
if(n==1) return 1;
return fibon (n-2) + fibon(n-1);
}
Слайд 6Применение принципа «Разделяй и властвуй» для поиска максимума массива
int q[10]=
{4, 3, 1, 8, 9, 10, 7, 2, 6, 5};
………………
int max (int, int); - прототип функции
void main (void)
{
int m, l = 0, r = 9;
…………….
for (int i = 0; i<10; i++) fprintf (fout, “%d…”, a[i]);
m = max (l, r);
……………
}
int max (int l, int r);
{
int mid, n, v
if (l == r) return a[l]; - ограничение рекурсии
mid = (l + r)/2;
n = max (l, mid);
v = max (mid+1, r);
if (n > v) return n;
else return v;
}
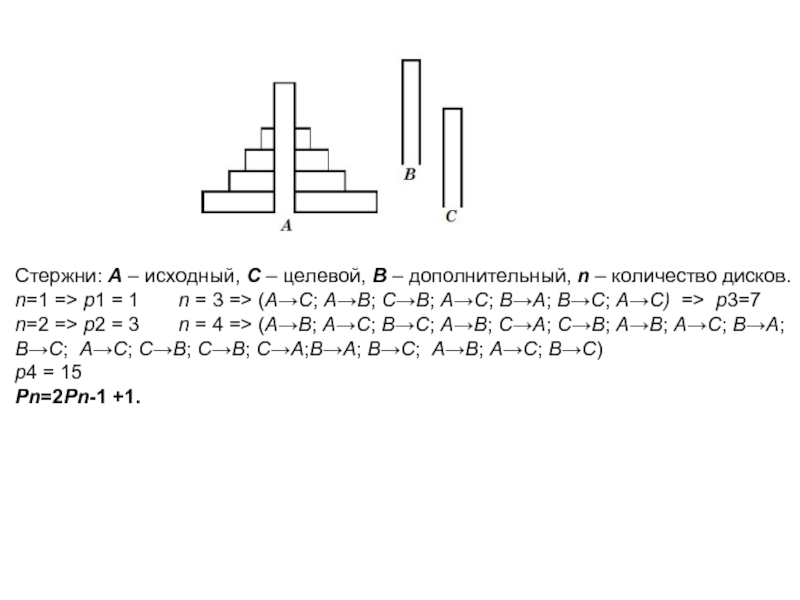
Слайд 10Стержни: А – исходный, С – целевой, В – дополнительный, n
– количество дисков.
n=1 => p1 = 1 n = 3 => (A→С; A→B; C→B; A→C; B→A; B→C; A→C) => р3=7
n=2 => p2 = 3 n = 4 => (A→B; A→C; B→C; A→B; C→A; C→B; A→B; A→C; B→A;
В→C; A→C; C→B; C→B; C→A;B→A; B→C; A→B; A→C; B→C) p4 = 15 Pn=2Pn-1 +1.
В→C; A→C; C→B; C→B; C→A;B→A; B→C; A→B; A→C; B→C) p4 = 15 Pn=2Pn-1 +1.
Слайд 11Программная реализация
void main()
{ . . .
put_disk( n, ’A’, ‘B’,
‘C’);
. . .
}
void put_disk(int n, char s1, char s2, char s3)
{ if (n == 1) //последняя перестановка единственного диска
printf (“%c --->%c \n", s1, s3);
else
{//Всю верхушку башни, кроме самого большого диска, перекладываем
// на свободный стержень (временно используется для этого s2)
put_disk(n - 1, s1, s3, s2); //s1->s2 через s3
//Самый большой диск кладём на 'место назначения'
printf (“%c --->%c \n", s1, s3);
//Перекладываем на него все остальные, используя
освободившийся стержень
put_disk(n-1,s2,s1,s3); //s2->s3 через s1
}
}
. . .
}
void put_disk(int n, char s1, char s2, char s3)
{ if (n == 1) //последняя перестановка единственного диска
printf (“%c --->%c \n", s1, s3);
else
{//Всю верхушку башни, кроме самого большого диска, перекладываем
// на свободный стержень (временно используется для этого s2)
put_disk(n - 1, s1, s3, s2); //s1->s2 через s3
//Самый большой диск кладём на 'место назначения'
printf (“%c --->%c \n", s1, s3);
//Перекладываем на него все остальные, используя
освободившийся стержень
put_disk(n-1,s2,s1,s3); //s2->s3 через s1
}
}




![Применение принципа «Разделяй и властвуй» для поиска максимума массива int q[10]= {4, 3, 1, 8,](/img/tmb/1/7143/d346627c9d632bcdae211f8b0f30a73e-800x.jpg)