Р.Н.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Рекурсия. Сложность алгоритмов презентация
Содержание
- 1. Рекурсия. Сложность алгоритмов
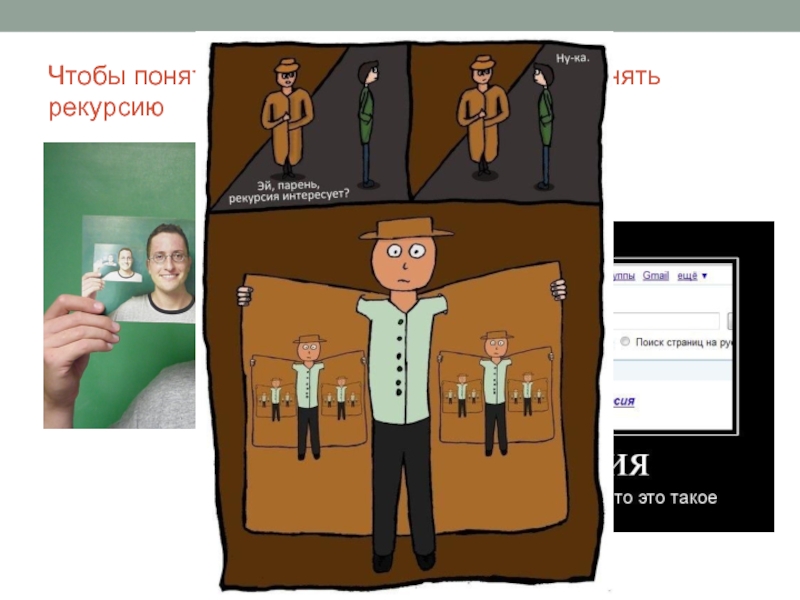
- 2. Чтобы понять рекурсию, …нужно сначала понять рекурсию
- 3. Чтобы понять рекурсию, …нужно сначала понять
- 4. { ... = НОД( Math.Max(A,
- 5. { if (!путь_из_(1, 1))
- 6. Обход конём [не]шахматной доски int[] dx =
- 7. Мат. анализ: «О» большое Пишется: f(x) =
- 8. Сложность алгоритмов Говорят: «Сложность алгоритма есть O(N2)»
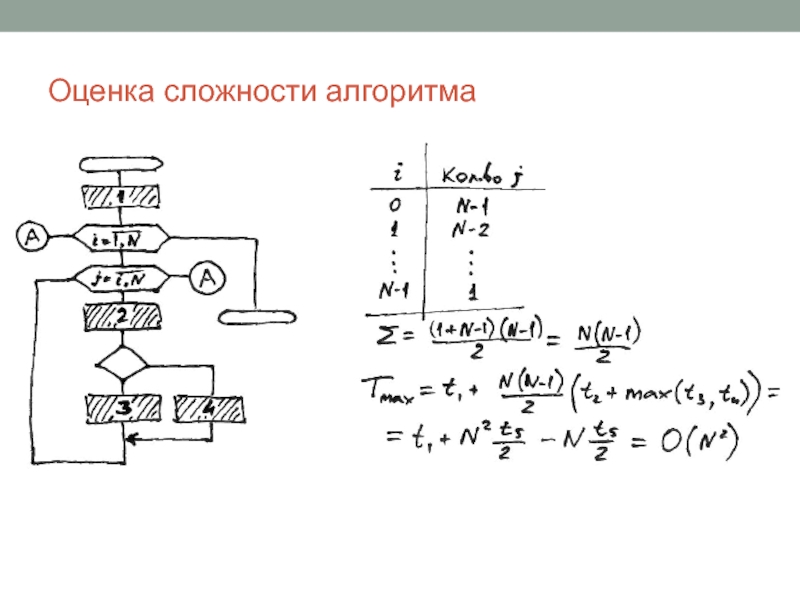
- 9. Оценка сложности алгоритма
Чтобы понять рекурсию, …нужно сначала понять рекурсию
Слайд 1Программирование
на языке высокого уровня
Лекция 13.
Рекурсия. Сложность алгоритмов
Кафедра АСОИУ ОмГТУ, 2013
Богатов
Слайд 3
Чтобы понять рекурсию, …нужно сначала понять рекурсию
Рекурсия — см. Рекурсия.
Рекурсивная функция
— функция, которая определяется через себя же.
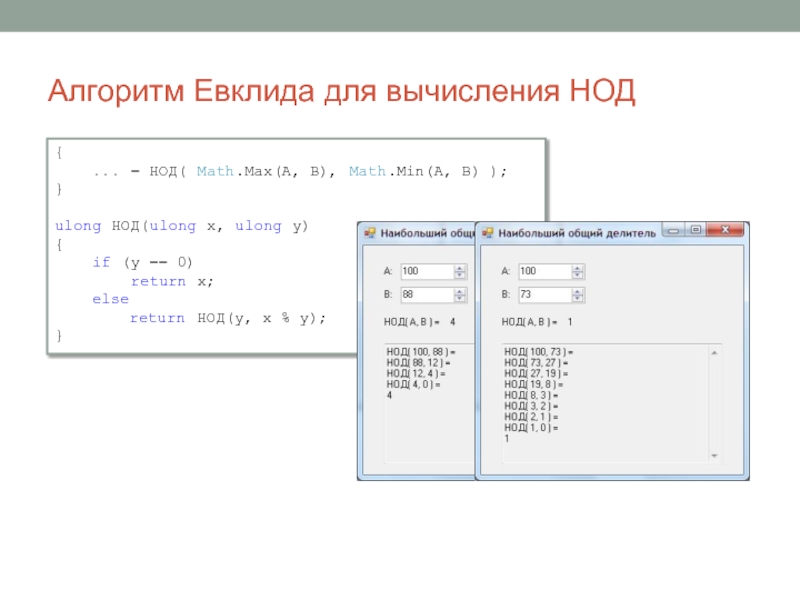
Слайд 4{
... = НОД( Math.Max(A, B), Math.Min(A, B) );
}
ulong НОД(ulong
x, ulong y)
{
if (y == 0)
return x;
else
return НОД(y, x % y);
}
{
if (y == 0)
return x;
else
return НОД(y, x % y);
}
Алгоритм Евклида для вычисления НОД
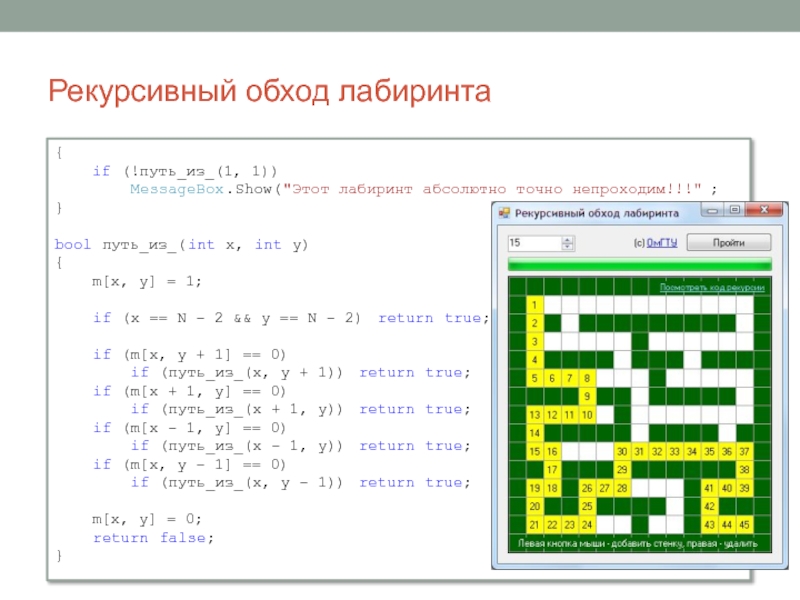
Слайд 5{
if (!путь_из_(1, 1))
MessageBox.Show("Этот лабиринт абсолютно
точно непроходим!!!";
}
bool путь_из_(int x, int y)
{
m[x, y] = 1;
if (x == N - 2 && y == N - 2) return true;
if (m[x, y + 1] == 0)
if (путь_из_(x, y + 1)) return true;
if (m[x + 1, y] == 0)
if (путь_из_(x + 1, y)) return true;
if (m[x - 1, y] == 0)
if (путь_из_(x - 1, y)) return true;
if (m[x, y - 1] == 0)
if (путь_из_(x, y - 1)) return true;
m[x, y] = 0;
return false;
}
}
bool путь_из_(int x, int y)
{
m[x, y] = 1;
if (x == N - 2 && y == N - 2) return true;
if (m[x, y + 1] == 0)
if (путь_из_(x, y + 1)) return true;
if (m[x + 1, y] == 0)
if (путь_из_(x + 1, y)) return true;
if (m[x - 1, y] == 0)
if (путь_из_(x - 1, y)) return true;
if (m[x, y - 1] == 0)
if (путь_из_(x, y - 1)) return true;
m[x, y] = 0;
return false;
}
Рекурсивный обход лабиринта
Слайд 6Обход конём [не]шахматной доски
int[] dx = new int[] { 1, 2,
2, 1, -1, -2, -2, -1 };
int[] dy = new int[] { -2, -1, 1, 2, 2, 1, -1, -2 };
void прыгнуть_в_(int x, int y)
{
Доска[x + 2, y + 2] = ход;
if (ход == последний) решений++;
else
{
ход++;
// перебираем ячейки под ударом
for (int i = 0; i < 8; i++)
if (Доска[x + 2 + dx[i], y + 2 + dy[i]] == 0)
прыгнуть_в_(x + dx[i], y + dy[i]);
ход-;
}
Доска[x + 2, y + 2] = 0;
}
int[] dy = new int[] { -2, -1, 1, 2, 2, 1, -1, -2 };
void прыгнуть_в_(int x, int y)
{
Доска[x + 2, y + 2] = ход;
if (ход == последний) решений++;
else
{
ход++;
// перебираем ячейки под ударом
for (int i = 0; i < 8; i++)
if (Доска[x + 2 + dx[i], y + 2 + dy[i]] == 0)
прыгнуть_в_(x + dx[i], y + dy[i]);
ход-;
}
Доска[x + 2, y + 2] = 0;
}
Слайд 7Мат. анализ: «О» большое
Пишется: f(x) = O(g(x))
Читается: f является «О» большим
от g
Формальное определение: f(x) = O(g(x)), если Ǝ x0 и c0 | f(x) < c0g(x) при x > x0
Формальное определение: f(x) = O(g(x)), если Ǝ x0 и c0 | f(x) < c0g(x) при x > x0
Слайд 8Сложность алгоритмов
Говорят: «Сложность алгоритма есть O(N2)»
Значит: при больших N время
работы алгоритма (или количество операций) не более чем c∙N2, где c – положительная константа
N – обычно объём входных данных
N – обычно объём входных данных
