- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Re-definition of the generator презентация
Содержание
- 1. Re-definition of the generator
- 2. GOALS FOR A GENERATOR We have defined
- 3. GOALS FOR A GENERATOR Speed Ability to
- 4. GOALS FOR A GENERATOR Expressivity & Diversity
- 5. TAXONOMY Togelius et al. set a Taxonomy
- 6. TAXONOMY Online v. Offline Location of the
- 7. TAXONOMY Generic v. Adaptive Does it adapt
- 8. EXAMPLE TAXA Faster than Light Online Necessary
- 11. QUICK AND DIRTY SUMMARY Class is biomodal
- 12. WHY THIS COURSE Interested/Interesting Perspective area of
- 13. RETURN Implementation of skills Examples Advantages and Disadvantages
- 14. PORTFOLIO 2 Elements @ 20% each 4
- 15. TEXTURES AND LANDSCAPES
- 17. SPECTRUM OF NEED Flight Simulation Non-consequential to
- 18. SPECTRUM OF NEED FPS Somewhat Essential
- 19. REPRESENTATION Intensity and Height Maps Grid of Values
- 20. PURE RANDOMNESS For each square – take
- 21. FORCED TO BE SMOOTH -INTERPOLATION Real terrain
- 23. LATTICE SIZE Larger Lattice – Places large
- 24. BILINEAR Weighted Average coming from the value
- 25. ALSO WORKS FOR TEXTURES
- 26. BICUBIC Linear is perhaps not as realistic,
- 27. BICUBIC Example x=1 10% distance of the
- 28. MOVING PAST DIRECT GENERATORS Idea till now
- 29. AGENT GENERATION
- 30. DORAN AND PARBERRY 2010 Use the definition
- 31. INITIAL STATE Flat World bellow a waterline
- 32. COASTLINE AGENT Starts with a seed location,
- 33. COASTLINE AGENT When done subdivision will begin
- 34. SMOOTHING AGENT Makes a random walk about
- 35. BEACH AGENTS Search the area on the
- 37. MOUNTAIN AGENTS Starts at a random location
- 38. HILL AGENTS Similar to Mountain agents Expend
- 39. RIVER AGENTS Begin on the coastline Will
- 41. ASHLOCK AND MCGUINESS 2013 Evolutionary Approach to
- 42. METHOD Recursive quartering of the map space
- 43. AUTOMATION Representation is an automation of transitions
- 44. EA SYSTEM Create a randomized population made
- 45. CROSSOVER IN A GA ON STRINGS One
- 46. CROSSOVER AND MUTATION OPERATIONS Treats the structure
- 47. EVALUATION AGAINST A TARGET
- 49. BEYOND SQUARES Hex based Games instead of squares Height map values -> biomes
- 50. CIV 5?
- 51. FACTALS
- 52. FRACTALS Self Similar Mathematical Structures Recursive Definitions
- 53. KOCH CURVE Each line has a triangle
- 54. MIDPOINT DISPLACEMENT FRACTAL Midpoint_Displacement(Startx,Endx,Run) Select the midpoint Midx
- 55. Iteration 0
- 56. DIAMOND SQUARE ALGORITHM Fournier et al. (1982),
- 57. DIAMOND-SQUARE Average over the 4 points (3
- 58. DSFACTAL DSFractal(startx,starty,endx,endy,run) midx
- 59. Square Diamond Square Diamond
- 60. TORUS x Mod Xn y Mod Yn
- 61. BROWN ET AL. (2011) Fractal Photomosaic
- 63. MOSACS Coloured Shards of Pottery, Stone, or
- 64. PHOTO MOSAICS First algorithmic version by R.
- 65. MAKING A PHOTO MOSAIC Break Images into
- 66. LENNA IMAGE Scanned in from a Playboy
- 69. MANDELBROT SET
- 71. DATA STRUCTURE X,Y values of the location
- 72. COLOURING Colouring based on the escape value
- 73. SEARCH THROUGH FRACTALS Genetic Algorithm Image Structure
- 74. EXPANDING ON THESE TECHNIQUES Target v. generation
Слайд 2GOALS FOR A GENERATOR
We have defined the process mechanically, but what
In Procedural Content Generation for Games a set of desirable traits for a generator to have are discussed. A good generation must meet with requirements of:
Speed
Reliability
Controllability
Expressivity & Diversity
Creativity & Believability
Слайд 3GOALS FOR A GENERATOR
Speed
Ability to have content not slow the game
Reliability
The Generator must meet with the constraints placed upon it, not introduce game breaking aspects
Level without an exit v. Flower with lopsided petals
Controllability
Ability of a human designer or algorithmic method to specify aspects of the generation
This level must have 5 enemies which are suitable to be faced by a level 10 Wizard or a level 4 Barbarian
Слайд 4GOALS FOR A GENERATOR
Expressivity & Diversity
The generated assets should not be
A number of different but equally relevant content
Hard to Measure (Defined Objective Measure)
Creativity & Believability
The generation should not feel `different` from one produced by a designer
Again Hard to Measure Objectively
Слайд 5TAXONOMY
Togelius et al. set a Taxonomy on how a generation can
Online v. Offline
Necessary v. Optional
Degree and Dimensions of Control
Generic v. Adaptive
Stochastic v. Deterministic
Constructive v. Generate and Test
Automatic v. Mixed Construction
Слайд 6TAXONOMY
Online v. Offline
Location of the generation on the host machine during
Necessary v. Optional
Generator builds key mechanical parts of the game or is it to increase the functionality
Degree and Dimensions of Control
The level to which a developer or player has input into the generation method
Слайд 7TAXONOMY
Generic v. Adaptive
Does it adapt to the player’s actions or will
Stochastic v. Deterministic
The generated content uses a random element in it’s creation or not
Constructive v. Generate and Test
The algorithm creates a or uses a search based approach
Automatic v. Mixed Construction
Does the generator act as the only designer or does a human designer use it as a tool
Слайд 8EXAMPLE TAXA
Faster than Light
Online
Necessary
Little Control
Generic
Stochastic
Constructive
Automatic
Speed Tree
Offline
Optional
Large Control
Generic
Deterministic
Constructive
Mixed
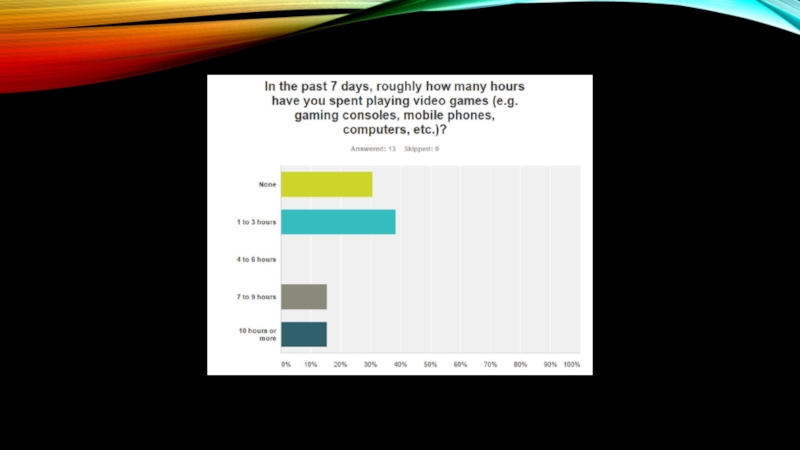
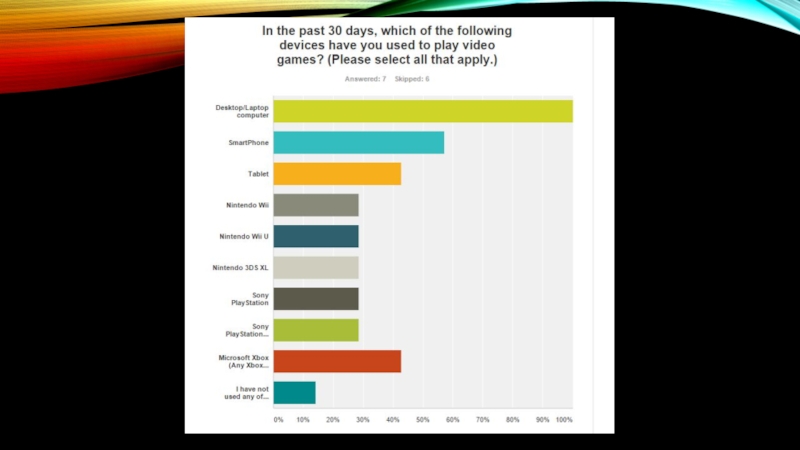
Слайд 11QUICK AND DIRTY SUMMARY
Class is biomodal in their time playing games
Large
PC gamers and cellphone games
Low usage of Consoles
Слайд 12WHY THIS COURSE
Interested/Interesting
Perspective area of employment
Understand why this technique is not
Слайд 14PORTFOLIO
2 Elements @ 20% each
4 Categories
Implement a research paper
Implement a small
Implement a PCG method for a new creative domain outside of games
Implement basic Maze/Texture generations and make comparisons
Both Elements due on May 1
Can ask for an examination before with no penalty in order to know what to improve upon
Слайд 17SPECTRUM OF NEED
Flight Simulation
Non-consequential to gameplay mechanics
Pure Aesthetics but low detail
Allows
Little Restriction on Player Movement
Open World FP
Essential to gameplay mechanics
Aesthetics are important for a local detail
On demand generation ability limited (Object Persistence)
Some Restrictions on Player Movement
Слайд 18SPECTRUM OF NEED
FPS
Somewhat Essential to Gameplay mechanics
Aesthetics are important for
On demand generation ability limited (Object Persistence)
Large Restrictions on Player Movement
RTS
Essential to Gameplay Mechanics
Aesthetics are not as important
No on-demand generation ability
Defines tactics of movement
Слайд 20PURE RANDOMNESS
For each square – take a number from a random
Problems
You get spikes in all the wrong places
Doesn’t hold with reality
Unplayable for games
Слайд 21FORCED TO BE SMOOTH -INTERPOLATION
Real terrain is not random - smoother
Idea
Calculate the intermediary points to fit with the grid
Loss of some features
We cannot make shear rock faces easily
Слайд 23LATTICE SIZE
Larger Lattice – Places large peaks and valleys
Smaller Lattice –
Hybrid – A larger lattice which determines the location of smaller lattices
Assume for the next set that our Lattice contains a 11x11 square of the total map
Ex. Between Height[0,0] to Height[10,10]
Move over the space, vertically or horizontally, and interpolate the other points
Слайд 24BILINEAR
Weighted Average coming from the value of both points, interpolate the
Height[0,y] = (10-y)/10 Height[0,0] + (y)/10 Height[0,10]
Height[10,y] = (10-y)/10 Height[10,0] + (y)/10 Height[10,10]
We now have the linear interpolation for the Y direction, we now make a second linear interpolation for the X for the remainder
Height[x,y] = (10-x)/10 Height[0,y] + (x)/10 Height[10,y]
Слайд 26BICUBIC
Linear is perhaps not as realistic, we want a smooth transition
Transition equation was a linear calculation, keep the same basic method but edit the equation
Slope Function in Bilinear is S(x)=x
Common slope function S(x)=-2x3+3x2
Слайд 27BICUBIC
Example x=1
10% distance of the slope face
S(.1) = .028
2.8% up
Height[0,y] = S(.1)y Height[0,0] + (1-S(.1))y Height[0,10]
Height[0,y] = (.972)y Height[0,0] + (.028)y Height[0,10]
Слайд 28MOVING PAST DIRECT GENERATORS
Idea till now have been to generate the
Alternative – place slopes directly
Interpolation leads to breaks along the lines of the lattice – the lattice becomes visible
The lattice can be formed to meet with the gradients
Слайд 30DORAN AND PARBERRY 2010
Use the definition of an agent as:
Agents perceives
Number of types of agents with different effector goals
Coastline Agents
Smoothing Agents
Beech Agents
Mountain Agents
River Agents
Each of these agents is given a number of tokens which they expend to change the environment
An agent without tokens dies
Слайд 31INITIAL STATE
Flat World bellow a waterline
Representation as a height map
A single
Слайд 32COASTLINE AGENT
Starts with a seed location, a preferred direction (repulsor, attactor
Capable of Producing Other Agents
Bifocates
Hands them a set of tokens (reducing its own)
New agent is given a different repulsor and attactor
Scores a point in the map P by dr(P)-da(P)+3de(P)
Dr – square of the distance to the repulsor
Da – square of the distance to the attractor
De – square of the distance to the edges
Wants to move close to the center
Слайд 33COASTLINE AGENT
When done subdivision will begin to spend tokens
Selects a random
The point with the highest score is filled in as part of the island
Process continues till all tokens are spent
Слайд 34SMOOTHING AGENT
Makes a random walk about the space and changes a
Слайд 35BEACH AGENTS
Search the area on the coastline and reduce their height
Has
Mountains beside the water will form cliffs
Makes random walks inland and will not progress father than a limit
Beaches should not extend in too deep
Слайд 37MOUNTAIN AGENTS
Starts at a random location and has a preferred direction
Will move toward that point rising the land like a V to either side of the walk
Will continue on their path unless blocked by water
Слайд 38HILL AGENTS
Similar to Mountain agents
Expend more tokens for each increase in
Слайд 39RIVER AGENTS
Begin on the coastline
Will walk from the coastline to a
Will stop their walk
if the mountain is too far away
If the mountain is too close
If there is no uphill or equal point ahead
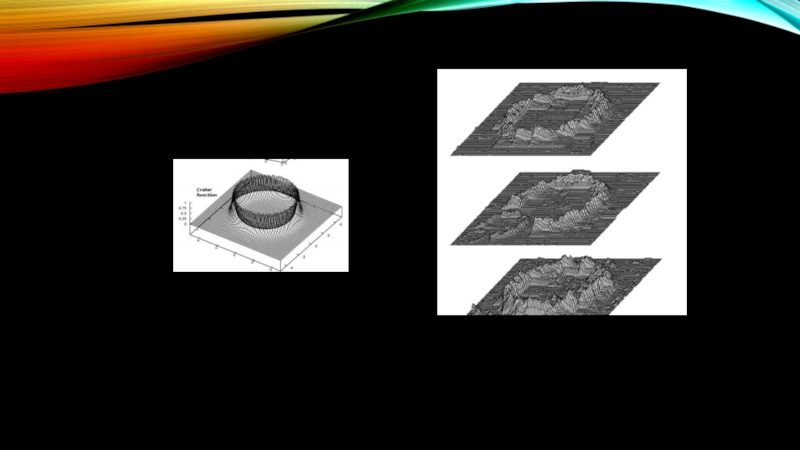
Слайд 41ASHLOCK AND MCGUINESS 2013
Evolutionary Approach to Landscapes
Matches a Target functions –
Allows for variation about this idea
Limited Application unless there is a placement of landscape ideals
Create a number of functions with desired properties (craters, mountains, rivers)
Merge these functions via some method F=Max(f1,f2,f3,…,fn)
Use the evolution to ensure a ‘interesting skinning’
Huge space savings – hold an agent not the texture
Слайд 42METHOD
Recursive quartering of the map space
Automation holds a state for each
The automation recusively calls itself in each location applying first an increase to the affected area equal to the automation value times the current multipliers
Multipliers are <1, it will progressively make smaller changes to smaller areas
Final height map is then interpolated
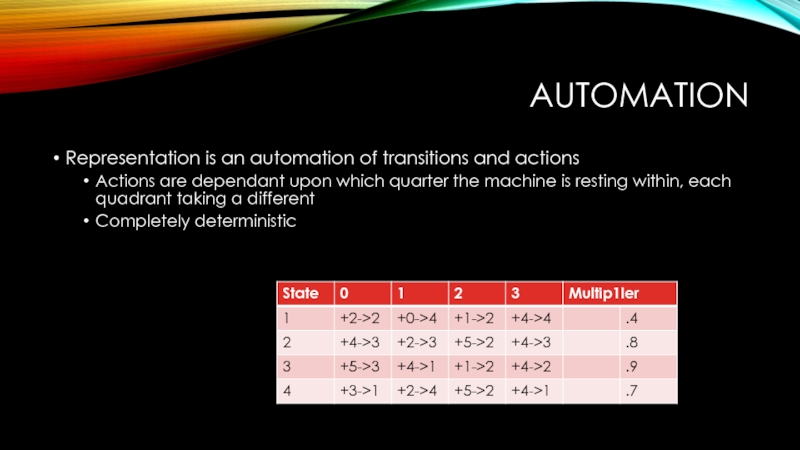
Слайд 43AUTOMATION
Representation is an automation of transitions and actions
Actions are dependant upon
Completely deterministic
Слайд 44EA SYSTEM
Create a randomized population made up of chromosomes, data structures
Until
Find an objective/fitness score for each member of the population
Select members to act upon using some variation operators
Apply operations on the members
Crossover
Mutations
Replace some members of the population with these children from the variation operators
Keep some members from the previous population in the new population, i.e. elitism/inheritance
Слайд 45CROSSOVER IN A GA ON STRINGS
One Point – Select One Point
Two Point – Select Two Point at Random and Swap
Uniform Order – Swap all with Probability of .5
Слайд 46CROSSOVER AND MUTATION OPERATIONS
Treats the structure as linear about states
Two point
Mutations change state transitions and make small changes to the multiplier in the range [-0.1,0.1]
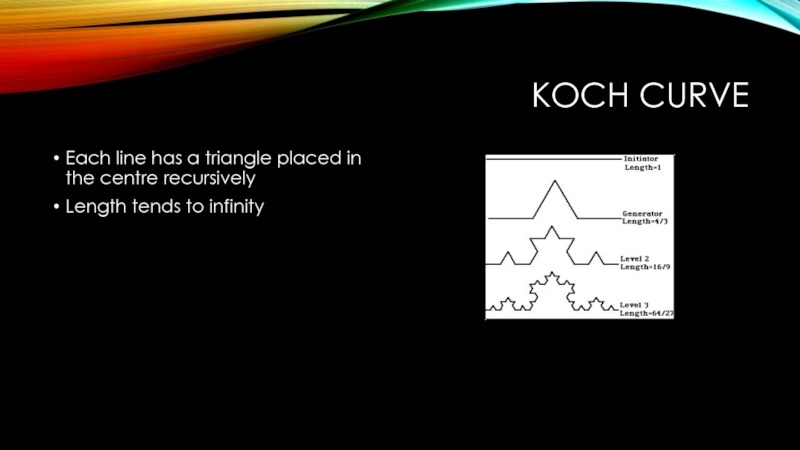
Слайд 52FRACTALS
Self Similar Mathematical Structures
Recursive Definitions
Create structures which have interesting complexity from
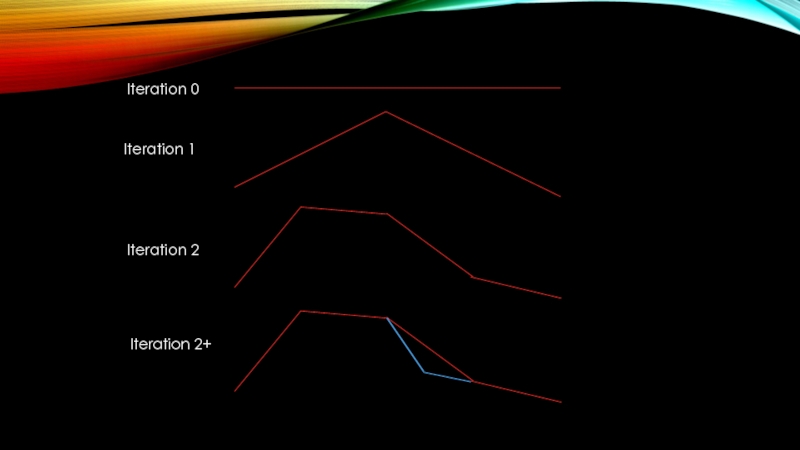
Слайд 54MIDPOINT DISPLACEMENT FRACTAL
Midpoint_Displacement(Startx,Endx,Run)
Select the midpoint
Midx
Midx.height = Midx.height+RandD(Run);
Recuse over the two halves of the space
Midpoint_Displacement(Midx,Endx,Run+1)
Midpoint_Displacement(Startx,Midx,Run+1)
Can be made Iterative – pregen the run values
Слайд 56DIAMOND SQUARE ALGORITHM
Fournier et al. (1982), purposed for terrain by Gavin
Four Seeding Values - one on each corner of the generation space
Extension of the ideas from the midpoint displacement moving it into 3 dimensions
Слайд 57DIAMOND-SQUARE
Average over the 4 points (3 if on edge)
Add a random
Square-step
Find the midpoint of a square of points
Add a random value
Diamond Step
Find the midpoint of a diamond of points
Add a random value
Alternate between Diamonds and Squares
Слайд 60TORUS
x Mod Xn
y Mod Yn
Note in C/C++ that mod is defined
(v-1)+n Mod n
Слайд 61BROWN ET AL. (2011)
Fractal Photomosaic images
Idea – to tile an
Computer Art
Слайд 63MOSACS
Coloured Shards of Pottery, Stone, or Glass plastered to walls
Mathematical and
Слайд 64PHOTO MOSAICS
First algorithmic version by R. Silvers
Holds Patent on his
Thesis is Robert Silvers “Photomosaics: Putting Pictures in Their Place” MIT 1996.
Sub-picture Resolution
Colour and Semantic Channels
Слайд 65MAKING A PHOTO MOSAIC
Break Images into Blocks
Take a set of ‘photos’
This
For each block in the image, search through the set and test against the target for closeness
RMS Error
Structurally
Слайд 66LENNA IMAGE
Scanned in from a Playboy Centerfold Lena Söderberg in 1973
Commonly used test image in graphical processing
Canonical Test Image
512x512 pixels, human face
Has lead to some issues in the field regarding it as sexist
Lena attended the 50th Anniversary of the Society for Imaging Science and Technology
Слайд 71DATA STRUCTURE
X,Y values of the location of the start of the
L defining the length of the window – zoom
Two Values for each of the 3 colour channels to define the colouring algorithm
Multiplier
Adder
Слайд 72COLOURING
Colouring based on the escape value of the factal
Colouring is defined
Red Green Blue
0-255
128*cos(S*n*P)+127
Слайд 73SEARCH THROUGH FRACTALS
Genetic Algorithm
Image Structure in box and Colour – Defined
RMS error between pixel colour and
Each Box searched on separately
Builds the image box by box
Слайд 74EXPANDING ON THESE TECHNIQUES
Target v. generation
Animation of the process?
Growth into final
Cell Shaded Games
Alternative technique other than realistic
























![BICUBICExample x=110% distance of the slope faceS(.1) = .028 2.8% up the slopeHeight[0,y] = S(.1)y](/img/tmb/3/201747/3b744106ae15e7a7484e2f34b0b3d7d8-800x.jpg)