- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПЯВУ. Основы программирования. Лекция 7. Массив. Простейшие алгоритмы. Форматы вывода чисел презентация
Содержание
- 1. ПЯВУ. Основы программирования. Лекция 7. Массив. Простейшие алгоритмы. Форматы вывода чисел
- 2. Контрольные вопросы Что такое массив? Как объявить
- 3. Содержание Простейшие алгоритмы Алгоритм подсчета количества Алгоритм
- 4. Алгоритм подсчета количества Задача. Подсчитать количество элементов
- 5. Подсчет количества int n = 0;
- 6. Среднее арифметическое Задача. Найти среднее арифметическое элементов
- 7. Среднее арифметическое double sum = 0, avrg;
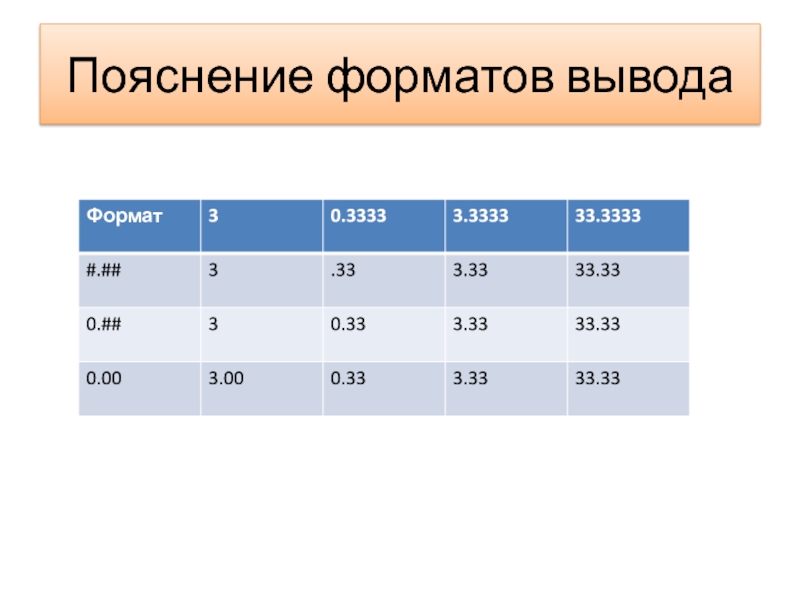
- 8. Пояснение форматов вывода
- 9. Алгоритм подсчета количества слов в строке Будем
- 10. Алгоритм подсчета количества слов. Флаг состояния Введем
- 11. Композиция алгоритмов Известные алгоритмы могут комбинироваться в
- 12. Поиск заданного элемента массива Задача. Найти номер
- 13. Поиск заданного элемента массива Задача. Найти номер
- 14. Упражнения Какие из изученных алгоритмов являются композицией
- 15. Сортировка массива Сортировка – расположение элементов массива
- 16. Алгоритм сортировки пузырьком Однократный проход for(int
- 17. Иллюстрация прохода 3 6 1 4 5 9 2 8 7
- 18. Иллюстрация прохода 3 6 1 4 5 9 8 2 7
- 19. Иллюстрация прохода 3 6 1 4 9 5 8 2 7
- 20. Иллюстрация прохода 3 6 1 9 4 5 8 2 7
- 21. Иллюстрация прохода 3 6 9 1 4 5 2 8 7
- 22. Иллюстрация прохода 3 9 6 1 4 5 2 8 7
- 23. Иллюстрация прохода 9 3 6 1 4 5 2 8 7
- 24. Сортировка пузырьком Всего однократный проход нужно применить
- 25. Сортировка пузырьком. Оптимизация. Количество итераций внутреннего цикла
- 26. Улучшенная сортировка пузырьком Количество итераций оригинального алгоритма
- 27. Анализ сортировки пузырьком Количество итераций = (N-1)+(N-2)+…+1
- 28. Циклические перестановки массива 1, 2, 3, 4,
- 29. Алгоритм циклической перестановки Против часовой стрелки:
- 30. Контрольные вопросы Что означает термин “Сортировка” в
- 31. Задачи Разработайте алгоритм инвертирования массива целых? (Инвертирование
Слайд 2Контрольные вопросы
Что такое массив?
Как объявить массив?
Как узнать количество элементов массива?
Как нумеруются
элементы массива?
Где применяется (в C#) и что означает слово break? continue?
Где применяется (в C#) и что означает слово break? continue?
Слайд 3Содержание
Простейшие алгоритмы
Алгоритм подсчета количества
Алгоритм нахождения сумы и среднего арифметического
Алгоритм подсчета количества
слов в строке
Форматы вывода чисел
Поиск элемента массива, удовлетворяющего заданному условию
Сортировка массива “пузырьком”
Алгоритм циклической перестановки массива
Форматы вывода чисел
Поиск элемента массива, удовлетворяющего заданному условию
Сортировка массива “пузырьком”
Алгоритм циклической перестановки массива
Слайд 4Алгоритм подсчета количества
Задача. Подсчитать количество элементов массива целых, делящихся на 3.
//Подготовим
пример исходных данных
Random r = new Random();
int [] a = new int[10];
for(int i = 0; i < a.Length; i++)
a[i] = r.Next(25);
for(int i = 0; i < a.Length; i++)
Console.Write(“{0}, ”, a[i]);
Console.WriteLine();
Random r = new Random();
int [] a = new int[10];
for(int i = 0; i < a.Length; i++)
a[i] = r.Next(25);
for(int i = 0; i < a.Length; i++)
Console.Write(“{0}, ”, a[i]);
Console.WriteLine();
Слайд 5Подсчет количества
int n = 0;
for(int i = 0; i
a.Length; i++)
if(a[i] % 3 == 0)
n++;
//Вывод результата для контроля
Console.WriteLine(“N = {0}”, n);
if(a[i] % 3 == 0)
n++;
//Вывод результата для контроля
Console.WriteLine(“N = {0}”, n);
Слайд 6Среднее арифметическое
Задача. Найти среднее арифметическое элементов массива действительных чисел.
//Подготовим пример исходных
данных
Random r = new Random();
double [] a = new double[10];
for(int i = 0; i < a.Length; i++)
a[i] = 10*r.NextDouble() - 5;
for(int i = 0; i < a.Length; i++)
Console.Write(“{0:0.##}, ”, a[i]);
Console.WriteLine();
Random r = new Random();
double [] a = new double[10];
for(int i = 0; i < a.Length; i++)
a[i] = 10*r.NextDouble() - 5;
for(int i = 0; i < a.Length; i++)
Console.Write(“{0:0.##}, ”, a[i]);
Console.WriteLine();
Слайд 7Среднее арифметическое
double sum = 0, avrg;
for(int i = 0; i
< a.Length; i++)
sum += a[i];
avrg = sum/a.Length;
//Вывод результата для контроля
Console.WriteLine(“Среднее = {0:0.##}”, avrg);
sum += a[i];
avrg = sum/a.Length;
//Вывод результата для контроля
Console.WriteLine(“Среднее = {0:0.##}”, avrg);
Слайд 9Алгоритм подсчета количества слов в строке
Будем считать, что строка имеет вид:
__ХХХХХХХ______ХХХХХХХ__...
Т.е.,
что состоит из слов и разделителей.
Что считать, начала слов или окончания?
__ХХХХХХХ__ __ХХХХХХХ__
Удобнее начала.
Что считать, начала слов или окончания?
__ХХХХХХХ__ __ХХХХХХХ__
Удобнее начала.
Слайд 10Алгоритм подсчета количества слов.
Флаг состояния
Введем булевскую переменную, которая будет определять, находимся
ли мы в слове или вне слова:
bool outOfWord = true;
0. Занулим счетчик слов n.
Цикл по всем символам строки ci
Если ci – разделитель, то outOfWord = true;
Иначе, если outOfWord истино (нашли начало слова), то outOfWord = false и увеличить счетчик слов.
Конец цикла.
bool outOfWord = true;
0. Занулим счетчик слов n.
Цикл по всем символам строки ci
Если ci – разделитель, то outOfWord = true;
Иначе, если outOfWord истино (нашли начало слова), то outOfWord = false и увеличить счетчик слов.
Конец цикла.
Слайд 11Композиция алгоритмов
Известные алгоритмы могут комбинироваться в совместный алгоритм для решения новой
задачи.
Задача. Подсчитать количество чисел массива больших среднего.
Вычислить среднее (avrg).
Подсчитать количество чисел, больших avrg.
Задача. Подсчитать количество чисел массива больших среднего.
Вычислить среднее (avrg).
Подсчитать количество чисел, больших avrg.
Слайд 12Поиск заданного элемента массива
Задача. Найти номер первого элемента массива удовлетворяющего заданному
условию, или установить, что такого элемента нет.
Задача уже решалась, как часть задачи “Поиск условного наибольшего”
Задача уже решалась, как часть задачи “Поиск условного наибольшего”
Слайд 13Поиск заданного элемента массива
Задача. Найти номер первого элемента массива делящегося на
3 или установить, что такого элемента нет.
int iFound = -1;
for(int i = 0; i < a.Length; i++)
if(a[i] % 3 == 0)
{
iFound = i;
break;
}
// Здесь в iFound содержится номер искомого элемента массива // или -1, если такого элемента нет
int iFound = -1;
for(int i = 0; i < a.Length; i++)
if(a[i] % 3 == 0)
{
iFound = i;
break;
}
// Здесь в iFound содержится номер искомого элемента массива // или -1, если такого элемента нет
Слайд 14Упражнения
Какие из изученных алгоритмов являются композицией других алгоритмов?
Подсчет количество слов в
строке.
Поиск наибольшего/наименьшего элемента массива.
Поиск элемента массива, удовлетворяющего заданному условию.
Подсчет количества элементов, удовлетворяющих заданному условию.
Поиск условно наибольшего/наименьшего элемента массива.
Поиск элементов массива больших среднего.
Какие из задач являются конкретизациями алгоритмов, приведенных выше?
Подсчитать количество пробелов в строке.
Найти первый наибольший среди элементов массива, которые делятся на 3.
Поясните, что означают коды форматирования # и 0.
Поиск наибольшего/наименьшего элемента массива.
Поиск элемента массива, удовлетворяющего заданному условию.
Подсчет количества элементов, удовлетворяющих заданному условию.
Поиск условно наибольшего/наименьшего элемента массива.
Поиск элементов массива больших среднего.
Какие из задач являются конкретизациями алгоритмов, приведенных выше?
Подсчитать количество пробелов в строке.
Найти первый наибольший среди элементов массива, которые делятся на 3.
Поясните, что означают коды форматирования # и 0.
Слайд 15Сортировка массива
Сортировка – расположение элементов массива в порядке возрастания или убывания.
Сортировка
– важная задача обработки информации. (Проще искать в отсортированном массиве: телефонный справочник, список группы и т.п.)
Имеются более 100 алгоритмов сортировки.
Имеются более 100 алгоритмов сортировки.
Слайд 16Алгоритм сортировки пузырьком
Однократный проход
for(int i = 0; i < a.Length -
1; i++)
if(a[i]>a[i + 1])
{
double x = a[i];
a[i] = a[i + 1];
a[i + 1] = x;
}
Самый большой элемент массива окажется последним. Т.е. он будет находиться на своем месте.
Останется отсортировать только первые a.Length-1 элементов.
if(a[i]>a[i + 1])
{
double x = a[i];
a[i] = a[i + 1];
a[i + 1] = x;
}
Самый большой элемент массива окажется последним. Т.е. он будет находиться на своем месте.
Останется отсортировать только первые a.Length-1 элементов.
Слайд 24Сортировка пузырьком
Всего однократный проход нужно применить N-1 раз, где N –
длина массива. (Массив из 1 элемента всегда отсортирован!)
for(int j = 1; j < a.Length; j++)
for(int i = 0; i < a.Length - 1; i++)
if(a[i]>a[i + 1])
{
double x = a[i];
a[i] = a[i + 1];
a[i + 1] = x;
}
Вложенные циклы
for(int j = 1; j < a.Length; j++)
for(int i = 0; i < a.Length - 1; i++)
if(a[i]>a[i + 1])
{
double x = a[i];
a[i] = a[i + 1];
a[i + 1] = x;
}
Вложенные циклы
Слайд 25Сортировка пузырьком. Оптимизация.
Количество итераций внутреннего цикла не зависит от номера итерации
внешнего цикла.
Было установлено, что неотсортированная часть массива после каждого прохода сокращается на 1 элемент.
Рассмотрим:
for(int j = 1; j < a.Length; j++)
for(int i = 0; i < a.Length - j; i++)
if(a[i]>a[i + 1])
{
double x = a[i];
a[i] = a[i + 1];
a[i + 1] = x;
}
Было установлено, что неотсортированная часть массива после каждого прохода сокращается на 1 элемент.
Рассмотрим:
for(int j = 1; j < a.Length; j++)
for(int i = 0; i < a.Length - j; i++)
if(a[i]>a[i + 1])
{
double x = a[i];
a[i] = a[i + 1];
a[i + 1] = x;
}
Слайд 26Улучшенная сортировка пузырьком
Количество итераций оригинального алгоритма не зависит от исходного порядка
элементов массива. (Даже если массив изначально упорядочен!)
Улучшенный пузырек:
for(int j = 1; j < a.Length; j++)
{
bool sorted = true;
for(int i = 0; i < a.Length - j; i++)
if(a[i]>a[i + 1])
{
double x = a[i];
a[i] = a[i + 1];
a[i + 1] = x;
sorted = false;
}
if(sorted)
break;
}
Улучшенный пузырек:
for(int j = 1; j < a.Length; j++)
{
bool sorted = true;
for(int i = 0; i < a.Length - j; i++)
if(a[i]>a[i + 1])
{
double x = a[i];
a[i] = a[i + 1];
a[i + 1] = x;
sorted = false;
}
if(sorted)
break;
}
Слайд 27Анализ сортировки пузырьком
Количество итераций = (N-1)+(N-2)+…+1
= N*(N-1)/2
Количество сравнений = N*(N-1)/2
Среднее количество
перестановок
= N*(N-1)/4
= N*(N-1)/4
Слайд 28Циклические перестановки массива
1, 2, 3, 4, 5
По часовой стрелке:
5, 1, 2,
3, 4
Против часовой стрелки:
2, 3, 4, 5, 1
Против часовой стрелки:
2, 3, 4, 5, 1
Слайд 29Алгоритм циклической перестановки
Против часовой стрелки:
int x = a[0];
for(int i = 1;
i < a.Length; i++)
a[i-1]=a[i];
a[a.Length-1] = x;
По часовой стрелке:
int x = a[a.Length-1];
for(int i = a.Length-1; i > 0; i--)
a[i]=a[i-1];
a[0] = x;
a[i-1]=a[i];
a[a.Length-1] = x;
По часовой стрелке:
int x = a[a.Length-1];
for(int i = a.Length-1; i > 0; i--)
a[i]=a[i-1];
a[0] = x;
Слайд 30Контрольные вопросы
Что означает термин “Сортировка” в информатике?
Зачем применяется сортировка?
От чего и
как зависит количество операций при сортировке пузырьком?
Как мог бы выглядеть алгоритм решения задачи: “Найти 5 наибольших элементов массива чисел”?
Как можно доработать алгоритм циклической перестановки, что бы перестановка осуществлялась на N позиций?
Как мог бы выглядеть алгоритм решения задачи: “Найти 5 наибольших элементов массива чисел”?
Как можно доработать алгоритм циклической перестановки, что бы перестановка осуществлялась на N позиций?
Слайд 31Задачи
Разработайте алгоритм инвертирования массива целых? (Инвертирование – расположение элементов в обратном
порядке, например, 1,2,3=>3,2,1)
Разработайте алгоритм “перетасовки” массива (как колоды карт). Например:1,2,3,4,5,6,7 после перетасовки должен с равной вероятностью принимать значение любой перестановки.
Поясните, почему любой элемент массива может в конце оказаться на любом месте.
3. Разработайте алгоритм, который для произвольной перестановки чисел 1,2,3,4,5,6,7 подсчитывает количество инверсий.
Говорят, что перестановка содержит инверсию, если больший элемент расположен левее меньшего. Например, перестановка 1,2,3,4,7, 5,6 содержит 2 инверсии: 7-5 и 7-6.
Замечание. Четность числа инверсий определяет четность перестановки!
Разработайте алгоритм “перетасовки” массива (как колоды карт). Например:1,2,3,4,5,6,7 после перетасовки должен с равной вероятностью принимать значение любой перестановки.
Поясните, почему любой элемент массива может в конце оказаться на любом месте.
3. Разработайте алгоритм, который для произвольной перестановки чисел 1,2,3,4,5,6,7 подсчитывает количество инверсий.
Говорят, что перестановка содержит инверсию, если больший элемент расположен левее меньшего. Например, перестановка 1,2,3,4,7, 5,6 содержит 2 инверсии: 7-5 и 7-6.
Замечание. Четность числа инверсий определяет четность перестановки!




![Подсчет количестваint n = 0; for(int i = 0; i < a.Length; i++) if(a[i] % 3](/img/tmb/6/507328/a165d7da7378633e458ced8515f8be32-800x.jpg)









![Алгоритм сортировки пузырькомОднократный проходfor(int i = 0; i < a.Length - 1; i++) if(a[i]>a[i + 1]) { double](/img/tmb/6/507328/e892cb2eb157e7d9533eaafdf5dd4210-800x.jpg)












![Алгоритм циклической перестановкиПротив часовой стрелки:int x = a[0];for(int i = 1; i < a.Length; i++) a[i-1]=a[i];a[a.Length-1]](/img/tmb/6/507328/6adb733d7fa8d34821e124fab1e49f5d-800x.jpg)







