- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Приближенные схемы. Задачи теории расписаний презентация
Содержание
- 1. Приближенные схемы. Задачи теории расписаний
- 2. Полиномиальная приближенная схема (PTAS)
- 3. Вполне полиномиальная приближенная схема (FPTAS)
- 4. Как построить PTAS Упрощение
- 5. Упрощение примера I. Первая
- 6. P2||Cmax J={1,..., n} – работы. {M1,
- 7. Нижняя оценка
- 8. Как упростить пример? ( I→ I# )
- 9. Оценка на оптимум Лемма 6.1
- 10. Доказательство Xi – размер всех маленьких работ,
- 11. Как решить упрощенный пример? Как много работ
- 12. Как вернуться к исходной задаче? Пусть σ#
- 13. Процедура ( σ#(I#)→ σ(I) ) Большие работы
- 14. Оценка качества
- 15. Алгоритм PTAS-1 Input ( J={1,..., n},
- 16. Точность алгоритма PTAS-1 Теорема 6.2
- 17. Разбиение пространства решений
- 18. Общая схема Разбиение на области. Выбор
- 19. P2||Cmax J={1,..., n} – работы. {M1,
- 20. Как разбить на области Big = {
- 21. Сколько получилось областей? Число больших работ ≤
- 22. Как выбрать «хорошего» представителя? Назначение больших работ
- 23. А хорош ли представитель? Если A(l) =T,
- 24. Алгоритм PTAS-2 Input ( J={1,..., n},
- 25. Точность алгоритма PTAS-2 Теорема 6.3
- 26. Структурирование работы алгоритма Основная идея рассмотреть точный,
- 27. P2||Cmax J={1,..., n} – работы. {M1,
- 28. Краткая запись решения Обозначим через σk допустимое
- 29. Алгоритм «Динамическое программирование» Input (
- 30. Трудоемкость алгоритма Координаты всех векторов целые числа
- 31. Как упростить множество векторов? Все вектора соответствуют
- 32. Отсев векторов Пусть два вектора [x1,y1] и
- 33. Алгоритм FPTAS Input ( J={1,..., n},
- 34. Трудоемкость алгоритма FPTAS Множество векторов в Vi#
- 35. Оценка на вектора в Vi и Vi#
- 36. Доказательство (по индукции) i =1: (x1/Δ ≤
- 37. Точность алгоритма FPTAS Теорема 6.5
- 38. Доказательство
- 39. Практика При построении PTAS-1 маленькие работы склеивались
Слайд 2Полиномиальная приближенная схема (PTAS)
Семейство приближенных алгоритмов для
задачи Π, {Aε}ε называется полиномиальной приближенной схемой, если алгоритм Aε ― (1+ε)-приближенный алгоритм и время его работы ограничено полиномом от размера входа при фиксированном ε.
Слайд 3Вполне полиномиальная приближенная схема (FPTAS)
Семейство приближенных алгоритмов
для задачи Π, {Aε}ε называется вполне полиномиальной приближенной схемой, если алгоритм Aε ― (1+ε)-приближенный алгоритм и время его работы ограничено полиномом от размера входа и 1/ε.
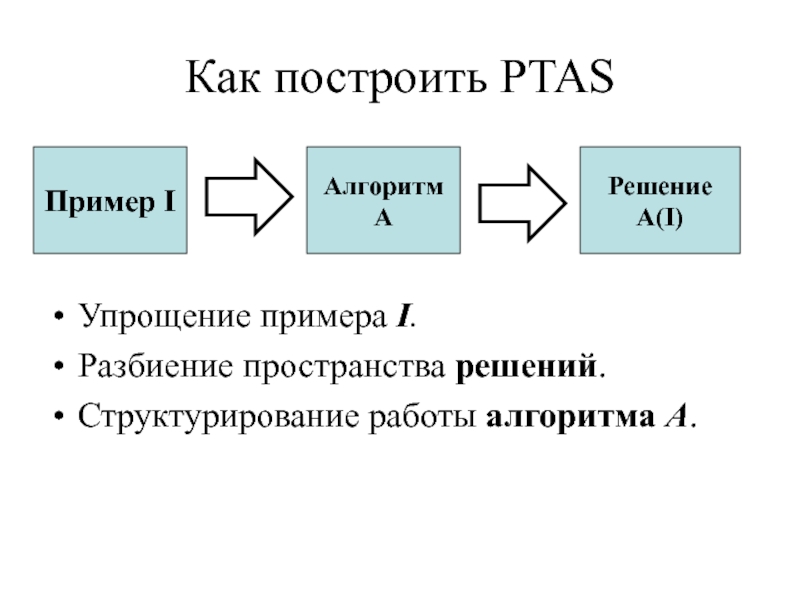
Слайд 4Как построить PTAS
Упрощение примера I.
Разбиение пространства решений.
Структурирование работы алгоритма A.
Пример
I
Алгоритм A
Решение A(I)
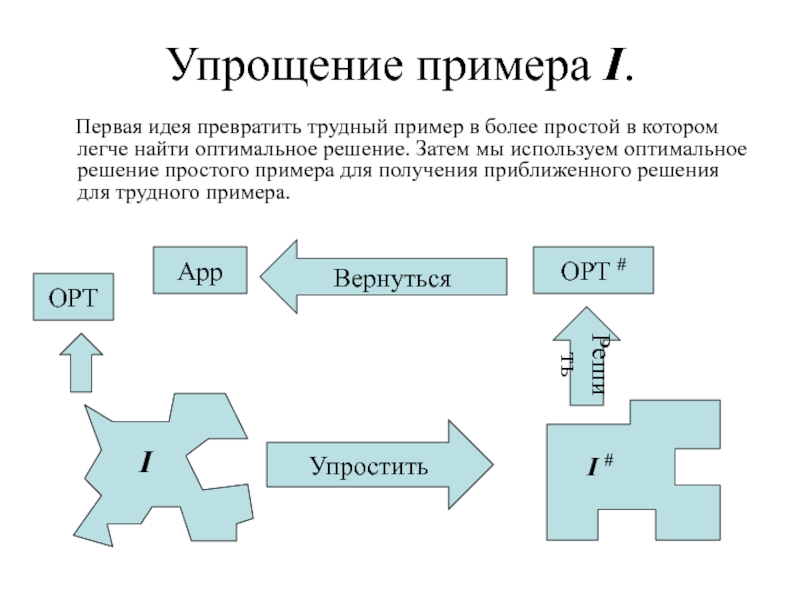
Слайд 5Упрощение примера I.
Первая идея превратить трудный пример в
более простой в котором легче найти оптимальное решение. Затем мы используем оптимальное решение простого примера для получения приближенного решения для трудного примера.
Упростить
Решить
OPT #
Вернуться
OPT
App
I
I #
Слайд 6P2||Cmax
J={1,..., n} – работы.
{M1, M2} – одинаковые машины.
j : pj
> 0 (i=1,…, n).
Каждая работа должна быть выполнена на одной из двух машин.
Минимизировать длину расписания (Cmax).
Прерывания запрещены.
Каждая машина обслуживает не более одной работы одновременно.
Каждая работа должна быть выполнена на одной из двух машин.
Минимизировать длину расписания (Cmax).
Прерывания запрещены.
Каждая машина обслуживает не более одной работы одновременно.
Слайд 8Как упростить пример? ( I→ I# )
Big = { j ∈
J| pj ≥ εL}
Новый пример I# содержит все большие работы из I.
Small = { j ∈ J| pj < εL}
Пусть X= Σj∈Small pj .
Новый пример I# содержит ⎣ X/εL ⎦ работ длины εL.
Маленькие работы, как бы склеиваются вместе и разрезаются на маленькие одинаковые кусочки.
Новый пример I# содержит все большие работы из I.
Small = { j ∈ J| pj < εL}
Пусть X= Σj∈Small pj .
Новый пример I# содержит ⎣ X/εL ⎦ работ длины εL.
Маленькие работы, как бы склеиваются вместе и разрезаются на маленькие одинаковые кусочки.
Слайд 10Доказательство
Xi – размер всех маленьких работ, выполняемых на машине Mi в
оптимальном расписании для I.
Оставим все большие работы на тех машинах, где они были в оптимальном расписании.
Заменим все маленькие работы на машине Mi на ⎡Xi /εL⎤ работ длины εL.
⎡X1 /εL⎤ + ⎡X2 /εL⎤ ≥ ⎣ X1 /εL + X2 /εL ⎦ = ⎣ X/εL ⎦
⎡Xi /εL⎤εL – Xi ≤ (Xi /εL + 1) εL – Xi ≤ εL
OPT(I#) ≤ OPT + εL ≤ (1+ ε)OPT(I)
Оставим все большие работы на тех машинах, где они были в оптимальном расписании.
Заменим все маленькие работы на машине Mi на ⎡Xi /εL⎤ работ длины εL.
⎡X1 /εL⎤ + ⎡X2 /εL⎤ ≥ ⎣ X1 /εL + X2 /εL ⎦ = ⎣ X/εL ⎦
⎡Xi /εL⎤εL – Xi ≤ (Xi /εL + 1) εL – Xi ≤ εL
OPT(I#) ≤ OPT + εL ≤ (1+ ε)OPT(I)
Слайд 11Как решить упрощенный пример?
Как много работ в I#?
pj ≥ εL для
всех работ в I#.
Общая длина всех работ в I# ≤ psum ≤ 2L.
Число работ в I# ≤ 2L/εL= 2/ε.
Число работ в I# не зависит от n!
Найдем все возможные расписания.
Число различных расписаний ≤ 22/ε !
Общая длина всех работ в I# ≤ psum ≤ 2L.
Число работ в I# ≤ 2L/εL= 2/ε.
Число работ в I# не зависит от n!
Найдем все возможные расписания.
Число различных расписаний ≤ 22/ε !
Слайд 12Как вернуться к исходной задаче?
Пусть σ# – оптимальное расписание для I#.
Li#
– нагрузка машины Mi в σ#.
Bi# – общая длина больших работ на Mi в σ#.
Xi#– размер всех маленьких работ на Mi в σ#.
Li# = Bi# + Xi#.
Bi# – общая длина больших работ на Mi в σ#.
Xi#– размер всех маленьких работ на Mi в σ#.
Li# = Bi# + Xi#.
Слайд 13Процедура ( σ#(I#)→ σ(I) )
Большие работы выполняются на той же машине,
что и в σ#.
Выделим интервал длины X1# + 2εL на машине M1 и X2# на машине M2.
Будем последовательно упаковывать маленькие работы в выделенный интервал на M1, пока не встретим работу, которая туда не поместится.
Оставшиеся маленькие работы упакуем в выделенный интервал на M2.
Выделим интервал длины X1# + 2εL на машине M1 и X2# на машине M2.
Будем последовательно упаковывать маленькие работы в выделенный интервал на M1, пока не встретим работу, которая туда не поместится.
Оставшиеся маленькие работы упакуем в выделенный интервал на M2.
Слайд 15Алгоритм PTAS-1
Input ( J={1,..., n}, p: J → Z+)
Определим Big
= { j ∈ J| pj ≥ εL} и Small = { j ∈ J| pj < εL}
Заменим все маленькие работы на машине Mi на ⎡X /εL⎤ работ длины εL.
Найдем оптимальное расписание σ# в новом примере I#, перебрав все допустимые назначения работ по машинам.
По расписанию σ# построим допустимое расписание σ исходной задачи, используя описанную выше процедуру ( σ#(I#)→ σ(I) ).
Output (σ )
Заменим все маленькие работы на машине Mi на ⎡X /εL⎤ работ длины εL.
Найдем оптимальное расписание σ# в новом примере I#, перебрав все допустимые назначения работ по машинам.
По расписанию σ# построим допустимое расписание σ исходной задачи, используя описанную выше процедуру ( σ#(I#)→ σ(I) ).
Output (σ )
Слайд 16Точность алгоритма PTAS-1
Теорема 6.2
Алгоритма PTAS-1 – (1+ε)-приближенный алгоритм для
задачи P2||Cmax.
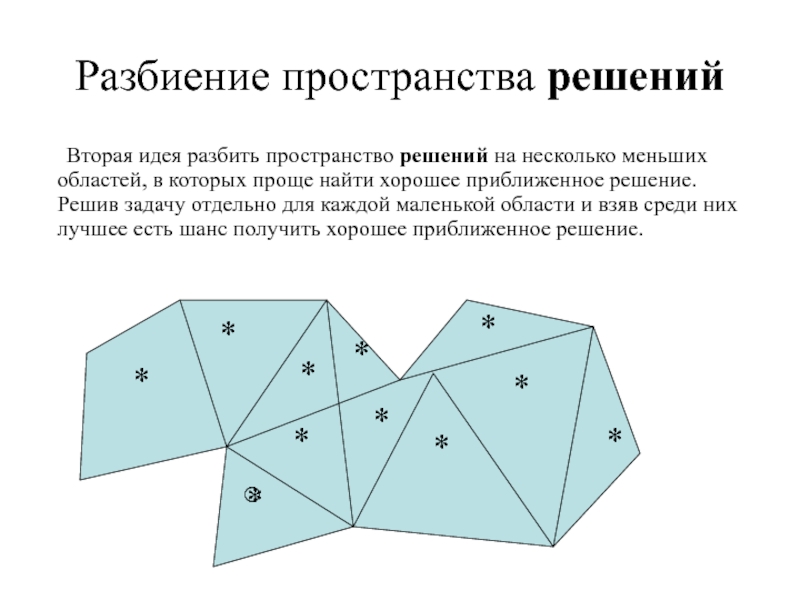
Слайд 17Разбиение пространства решений
Вторая идея разбить пространство решений
на несколько меньших областей, в которых проще найти хорошее приближенное решение. Решив задачу отдельно для каждой маленькой области и взяв среди них лучшее есть шанс получить хорошее приближенное решение.
*
*
*
*
*
*
*
*
*
*
*
○
Слайд 18Общая схема
Разбиение на области.
Выбор «хорошего» представителя в каждой области.
Выбор из
множества хороших представителей наилучшего.
Слайд 19P2||Cmax
J={1,..., n} – работы.
{M1, M2} – одинаковые машины.
j : pj
> 0 (i=1,…, n).
Каждая работа должна быть выполнена на одной из двух машин.
Минимизировать длину расписания (Cmax).
Прерывания запрещены.
Каждая машина обслуживает не более одной работы одновременно.
Каждая работа должна быть выполнена на одной из двух машин.
Минимизировать длину расписания (Cmax).
Прерывания запрещены.
Каждая машина обслуживает не более одной работы одновременно.
Слайд 20Как разбить на области
Big = { j ∈ J| pj ≥
εL}
Small = { j ∈ J| pj < εL}
Φ – множество допустимых расписаний
Расписание σ∈Φ – назначение работ на машины.
Определим области Φ(1), Φ(2),…согласно назначению больших работ: σ1 и σ2 лежат в одной области тогда и только тогда, когда каждая большая работа выполняется в σ1 на той же машине, что и в σ2.
Small = { j ∈ J| pj < εL}
Φ – множество допустимых расписаний
Расписание σ∈Φ – назначение работ на машины.
Определим области Φ(1), Φ(2),…согласно назначению больших работ: σ1 и σ2 лежат в одной области тогда и только тогда, когда каждая большая работа выполняется в σ1 на той же машине, что и в σ2.
Слайд 21Сколько получилось областей?
Число больших работ ≤ 2L/εL= 2/ε.
Число способов разместить большие
работы по двум машинам ≤ 22/ε.
Число различных областей ≤ 22/ε !
Число различных областей зависит от ε и не зависит от размера входа!
Число различных областей ≤ 22/ε !
Число различных областей зависит от ε и не зависит от размера входа!
Слайд 22Как выбрать «хорошего» представителя?
Назначение больших работ зафиксировано в Φ(l).
OPT(l) – длина
оптимального расписания в Φ(l).
Bi(l) – общая длина больших работ на Mi.
T := max{Bi(1), Bi(2)} ≤ OPT(l)
Пусть Bi(l) начальная загрузка машины Mi.
Назначим маленькие работы одну за другой по следующему правилу: каждый раз работа назначается на машину с меньшей нагрузкой на этот момент.
Полученное расписание σ(l) длины A(l) выберем представителем от Φ(l).
Bi(l) – общая длина больших работ на Mi.
T := max{Bi(1), Bi(2)} ≤ OPT(l)
Пусть Bi(l) начальная загрузка машины Mi.
Назначим маленькие работы одну за другой по следующему правилу: каждый раз работа назначается на машину с меньшей нагрузкой на этот момент.
Полученное расписание σ(l) длины A(l) выберем представителем от Φ(l).
Слайд 23А хорош ли представитель?
Если A(l) =T, то A(l) = OPT(l).
Пусть A(l)
>T.
Рассмотрим машину с большей загрузкой в σ(l).
Последняя назначенная на нее работа маленькая и ее длина меньше εL.
В момент назначения этой работы загрузка этой машины не превышала psum / 2.
A(l) ≤ (psum / 2) + εL ≤ (1 + ε)OPT ≤ (1 + ε)OPT(l)
Рассмотрим машину с большей загрузкой в σ(l).
Последняя назначенная на нее работа маленькая и ее длина меньше εL.
В момент назначения этой работы загрузка этой машины не превышала psum / 2.
A(l) ≤ (psum / 2) + εL ≤ (1 + ε)OPT ≤ (1 + ε)OPT(l)
Слайд 24Алгоритм PTAS-2
Input ( J={1,..., n}, p: J → Z+)
Определим
Big = { j ∈ J| pj ≥ εL} и Small = { j ∈ J| pj < εL}
Определим области Φ(1), Φ(2),…, Φ(h) согласно назначению больших работ по машинам.
Сформируем задачи I(1), I(2),…, I(h) , в которых назначение больших работ по машинам фиксировано и задано на входе.
Решим каждую из задач I(k) , k = 1,…,h, назначая маленькие работы одну за другой на машину с меньшей нагрузкой на текущий момент.
Пусть σ* - лучшее из полученных расписаний на шаге 4.
Output (σ* )
Определим области Φ(1), Φ(2),…, Φ(h) согласно назначению больших работ по машинам.
Сформируем задачи I(1), I(2),…, I(h) , в которых назначение больших работ по машинам фиксировано и задано на входе.
Решим каждую из задач I(k) , k = 1,…,h, назначая маленькие работы одну за другой на машину с меньшей нагрузкой на текущий момент.
Пусть σ* - лучшее из полученных расписаний на шаге 4.
Output (σ* )
Слайд 25Точность алгоритма PTAS-2
Теорема 6.3
Алгоритма PTAS-2 – (1+ε)-приближенный алгоритм для
задачи P2||Cmax.
Слайд 26Структурирование работы алгоритма
Основная идея рассмотреть точный, но медленный алгоритм.
Если алгоритм получает
и перерабатывает огромное количество различных значений, то мы можем отбросить часть из них и ускорить работу алгоритма.
Слайд 27P2||Cmax
J={1,..., n} – работы.
{M1, M2} – одинаковые машины.
j : pj
> 0 (i=1,…, n).
Каждая работа должна быть выполнена на одной из двух машин.
Минимизировать длину расписания (Cmax).
Прерывания запрещены.
Каждая машина обслуживает не более одной работы одновременно.
Каждая работа должна быть выполнена на одной из двух машин.
Минимизировать длину расписания (Cmax).
Прерывания запрещены.
Каждая машина обслуживает не более одной работы одновременно.
Слайд 28Краткая запись решения
Обозначим через σk допустимое расписание k первых работ {1,...,
k}.
Закодируем расписание σk с нагрузками машин L1 и L2 двумерным вектором [L1, L2].
Пусть Vk обозначает множество векторов, соответствующих допустимым расписаниям k первых работ {1,..., k}.
Закодируем расписание σk с нагрузками машин L1 и L2 двумерным вектором [L1, L2].
Пусть Vk обозначает множество векторов, соответствующих допустимым расписаниям k первых работ {1,..., k}.
Слайд 29Алгоритм «Динамическое программирование»
Input ( J={1,..., n}, p: J → Z+)
Положим V0={[0,0]}, i=0.
While i ≠ n do:
для каждого вектора [x,y]∈ Vi добавить вектора [x + pi ,y] и [x,y + pi ] в Vi+1;
i:= i +1;
3) Найти [x*,y*]∈ Vn , который минимизирует величину max [x,y]∈Vn{x,y}
Output ([x*,y*])
While i ≠ n do:
для каждого вектора [x,y]∈ Vi добавить вектора [x + pi ,y] и [x,y + pi ] в Vi+1;
i:= i +1;
3) Найти [x*,y*]∈ Vn , который минимизирует величину max [x,y]∈Vn{x,y}
Output ([x*,y*])
Слайд 30Трудоемкость алгоритма
Координаты всех векторов целые числа от 0 до psum.
Число различных
векторов в Vi ограничено (psum)2.
Общее количество векторов, вычисляемых алгоритмом не превосходит n(psum)2.
Трудоемкость алгоритма O(n(psum)2).
Размер входа |I| ограничен O(log(psum))=O(ln(psum)) или O(n log pmax).
Трудоемкость алгоритма не ограничена полиномом от размера входа!
Общее количество векторов, вычисляемых алгоритмом не превосходит n(psum)2.
Трудоемкость алгоритма O(n(psum)2).
Размер входа |I| ограничен O(log(psum))=O(ln(psum)) или O(n log pmax).
Трудоемкость алгоритма не ограничена полиномом от размера входа!
Слайд 31Как упростить множество векторов?
Все вектора соответствуют точкам плоскости в квадрате [0,
psum]×[0, psum].
Разделим этот квадрат вертикальными и горизонтальными линиями на клетки (квадратики).
В обоих направлениях линии имеют координаты Δi, где Δ = 1+ (ε/2n), i = 1, 2, …, K.
K = ⎡logΔ(psum)⎤= ⎡ln(psum)/ln Δ⎤= ⎡((1+2n )/ε) ln(psum)⎤
Разделим этот квадрат вертикальными и горизонтальными линиями на клетки (квадратики).
В обоих направлениях линии имеют координаты Δi, где Δ = 1+ (ε/2n), i = 1, 2, …, K.
K = ⎡logΔ(psum)⎤= ⎡ln(psum)/ln Δ⎤= ⎡((1+2n )/ε) ln(psum)⎤
Слайд 32Отсев векторов
Пусть два вектора [x1,y1] и [x2,y2] попали в одну клетку.
x1/Δ ≤ x2 ≤ x1Δ и y1/Δ ≤ y2 ≤ y1Δ .
Из каждой клетки, имеющей непустое пересечение с Vi , выберем один вектор и добавим его в «урезанное» множество векторов Vi#.
Слайд 33Алгоритм FPTAS
Input ( J={1,..., n}, p: J → Z+)
Положим
V0#={[0,0]}, i=0.
While i ≠ n do:
для каждого вектора [x,y]∈ Vi# добавить вектора [x + pi ,y] и [x,y + pi ] в Vi+1;
i:= i +1;
Преобразовать Vi в Vi#.
3) Найти [x*,y*]∈Vn# , который минимизирует величину max [x,y]∈Vn#{x,y}
Output ([x*,y*])
While i ≠ n do:
для каждого вектора [x,y]∈ Vi# добавить вектора [x + pi ,y] и [x,y + pi ] в Vi+1;
i:= i +1;
Преобразовать Vi в Vi#.
3) Найти [x*,y*]∈Vn# , который минимизирует величину max [x,y]∈Vn#{x,y}
Output ([x*,y*])
Слайд 34Трудоемкость алгоритма FPTAS
Множество векторов в Vi# содержит не более одного вектора
из каждой клетки.
Всего клеток K2.
Трудоемкость алгоритма FPTAS O(nK2).
nK2 = n⎡((1+2n )/ε) ln(psum)⎤2
Алгоритм FPTAS – полиномиален от размера входа и 1/ε.
Всего клеток K2.
Трудоемкость алгоритма FPTAS O(nK2).
nK2 = n⎡((1+2n )/ε) ln(psum)⎤2
Алгоритм FPTAS – полиномиален от размера входа и 1/ε.
Слайд 35Оценка на вектора в Vi и Vi#
Лемма 6.4
Для каждого вектора [x,y]∈ Vi существует вектор [x#,y#]∈ Vi# , такой что x# ≤ Δix и y# ≤ Δiy.
Слайд 36Доказательство (по индукции)
i =1: (x1/Δ ≤ x2 ≤ x1Δ и y1/Δ
≤ y2 ≤ y1Δ )
i ‒1 → i: Пусть [x,y]∈ Vi .
Тогда ∃ [a,b]∈ Vi-1 , и либо [x,y]= [a+pk,b], либо [x,y]= [a,b+pk].
Тогда ∃ [a#,b#]∈ : a# ≤ Δi ‒ 1a, b# ≤ Δi ‒ 1b .
Алгоритм FPTAS строит вектор [a#+pk ,b#] и выбирает [α,β], такой что α ≤ Δ(a#+pk ) и β ≤ Δb# .
Имеем α ≤ Δ(a#+pk ) ≤ Δi a + Δpk ≤ Δi(a+pk) =Δix и β ≤ Δiy.
i ‒1 → i: Пусть [x,y]∈ Vi .
Тогда ∃ [a,b]∈ Vi-1 , и либо [x,y]= [a+pk,b], либо [x,y]= [a,b+pk].
Тогда ∃ [a#,b#]∈ : a# ≤ Δi ‒ 1a, b# ≤ Δi ‒ 1b .
Алгоритм FPTAS строит вектор [a#+pk ,b#] и выбирает [α,β], такой что α ≤ Δ(a#+pk ) и β ≤ Δb# .
Имеем α ≤ Δ(a#+pk ) ≤ Δi a + Δpk ≤ Δi(a+pk) =Δix и β ≤ Δiy.
Слайд 37Точность алгоритма FPTAS
Теорема 6.5
Алгоритма FPTAS – (1+ε)-приближенный алгоритм для
задачи P2||Cmax.
Слайд 39Практика
При построении PTAS-1 маленькие работы склеивались в одну и разрезались на
одинаковые кусочки. Рассмотрим другой способ построения упрощенного примера. Рассмотрим множество маленьких работ. Если в нем есть две работы длины меньше чем εL склеим их, то есть две работы с длительностями p′, p′′ < εL заменим одной работой с длительностью p′ + p′′. Продолжим склеивание до тех пор пока в примере останется не больше одной работы с p < εL. Приведет ли такое упрощение к приближенной схеме?
Выполняется ли аналог леммы 6.1 ?
Можно ли оценить число работ в упрощенном примере ?
Как трансформировать оптимальное решение упрощенного примера в приближенное решение исходного примера?
Выполняется ли аналог леммы 6.1 ?
Можно ли оценить число работ в упрощенном примере ?
Как трансформировать оптимальное решение упрощенного примера в приближенное решение исходного примера?

























![Алгоритм «Динамическое программирование» Input ( J={1,..., n}, p: J → Z+) Положим V0={[0,0]}, i=0. While](/img/tmb/4/376090/2d5588cd4b7bdb0dbed6447357ef3ee0-800x.jpg)

![Как упростить множество векторов?Все вектора соответствуют точкам плоскости в квадрате [0, psum]×[0, psum].Разделим этот квадрат](/img/tmb/4/376090/8738ca7bc15bb31139e9e56503a6ce9d-800x.jpg)
![Отсев векторовПусть два вектора [x1,y1] и [x2,y2] попали в одну клетку. x1/Δ ≤ x2 ≤](/img/tmb/4/376090/53800c22191822003c24824a91becb5c-800x.jpg)
![Алгоритм FPTAS Input ( J={1,..., n}, p: J → Z+) Положим V0#={[0,0]}, i=0. While i](/img/tmb/4/376090/e1c373e1a8f3ea869a5b8adaba5bac0d-800x.jpg)

![Оценка на вектора в Vi и Vi# Лемма 6.4 Для каждого вектора [x,y]∈ Vi](/img/tmb/4/376090/37b14f9a80c4b3a92974c551427d4de2-800x.jpg)









