- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Представление и обработка чисел в компьютере презентация
Содержание
- 1. Представление и обработка чисел в компьютере
- 2. Система счисления- это правило записи чисел с
- 3. Перевод целых чисел из одной системы счисления
- 4. Способ 2 вытекает из соотношения (4.4); действия
- 5. Перевод дробных чисел из одной системы счисления
- 6. Если вновь позаимствовать в PASCAL'e обозначение функции
- 7. Понятие экономичности системы счисления Число в системе
- 8. Наиболее экономичной оказывается троичная система счисления,причем,
- 9. Для нахождения положения максимума нужно найти производную
- 10. Перевод чисел между системами счисления 2 ↔
- 11. Теорема 1. Для преобразования целого числа Zp
- 12. Вынесем множитель рr из всех слагаемых, у
- 13. Теорема 2. Для преобразования целого числа Zp
- 14. Преобразование нормализованных чисел Вещественное число X
- 15. Общий алгоритм нормализации можно изобразить в виде
- 16. Пусть, имеется число Хр = ±Мр
- 17. Различаются также ситуации kp ≥ 0 и
- 18. Кодирование чисел в компьютере и действия над
- 19. Кодирование и обработка в компьютере целых чисел
- 20. Сложение производится согласно таблице сложения, которая для
- 21. Кодирование и обработка в компьютере целых чисел
- 22. Кодирование и обработка в компьютере вещественных чисел
- 23. Следствие 2. Поскольку код вещественного числа в
- 24. Сложение нормализованных чисел Пусть имеются два
- 25. Умножение нормализованных чисел X1+X2 производится в соответствии
- 26. Общие замечания. 1)В компьютерах арифметические устройства
Слайд 2Система счисления- это правило записи чисел с помощью заданного набора специальных
Унарная-это система счисления,в которой для записи чисел используется только один знак - I(«палочка»). Следующее число получается из предыдущего добавлением новой I; их количество (сумма) равно самому числу.
Позиционными называются системы счисления, в которых значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр.
Общее количество входящих в него единиц,не зависит от способа его представления и остается одинаковым во всех системах счисления; различаются только формы представления одного и того же количественного содержания числа.
Система счисления с основанием 2 называется двоичной.Цифрами двоичной системы являются 0 и 1.
Слайд 3Перевод целых чисел из одной системы счисления
в другую
Два способа перевода целых
Способ 1 является следствием соотношений (4.3), из которых просматривается следующий алгоритм перевода:
целочисленное разделить исходное число (Z10) на основание новой системы счисления (q) и найти остаток от деления - это будет цифра 0-го разряда числа Zq;
частное от деления снова целочисленно разделить на q с выделением остатка; процедуру продолжать до тех пор, пока частное от деления не окажется меньше q;
образовавшиеся остатки от деления, поставленные в порядке, обратном порядку их получения, и представляют Zq.
Слайд 4Способ 2 вытекает из соотношения (4.4); действия производятся в соответствии со
1) определить т - 1 - максимальный показатель степени в представления числа по форме (4.1) для основания q;
2) целочисленно разделить исходное число (Z10) на основание новой системы счисления в степени т - 1 (т.е. qm-1 ) и найти остаток от деления; результат деления определит первую цифру числа Zq;
3) остаток от деления целочисленно разделить на qm-2 , результат деления принять за вторую цифру нового числа; найти остаток; продолжать эту последовательность действий, пока показатель степени q не достигнет значения 0.
Слайд 5Перевод дробных чисел из одной системы счисления
в другую.
Вещественное число, в общем
Правильную дробь в исходной системе счисления р будем записывать в виде 0, Yр; Дробь в системе q - 0, Yq, а преобразование - в виде 0, Yp → 0, Yq
Алгоритмы перевода 0,Y10→ 0,Yq выводится путем следующих рассуждений. Если основание системы счисления q, простая дробь содержит n цифр и bk - цифры дроби (1 ≤ k ≤ п, 0 ≤ bk ≤q -1), то она может быть представлена в виде суммы:
Часть дроби от разряда i до ее конца обозначим εi и примем εn = bn/q (очевидно, ε1 = О, Yq); тогда в (4.5) легко усматривается рекуррентное соотношение:
Слайд 6Если вновь позаимствовать в PASCAL'e обозначение функции - на этот раз
Соотношения (4.7) задают алгоритм преобразования 0, Y10→ 0,Yq:
умножить исходную дробь в 10-ной системе счисления на q, выделить целую часть - она будет первой цифрой новой дроби; отбросить целую часть;
для оставшейся дробной части операцию умножения с выделением целой и дробных частей повторять, пока в дробной части не окажется 0 или не будет достигнута желаемая точность конечного числа (exact); появляющиеся при этом целые будут цифрами новой дроби;
записать дробь в виде последовательности цифр после ноля с разделителем в порядке их появления .
Слайд 7Понятие экономичности системы счисления
Число в системе счисления р с k разрядами,
Количество разрядов числа при переходе от одной системы счисления к другой в общем случае меняется. Очевидно, если р = qσ (σ - не обязательно целое), то (Zp)max = pk - 1 = qσk - 1. Т.е. количество разрядов числа в системах счисления р и q будут различаться в σ раз. Очевидно соотношение:
Под экономичностью системы счисления будем понимать то количество чисел, которое можно записать в данной системе с помощью определенного количества цифр.
Слайд 8
Наиболее экономичной оказывается троичная система счисления,причем, результат будет тем же, если
Точное расположение максимума экономичности может быть установлено путем следующих рассуждений. Пусть имеется п знаков для записи чисел, а основание системы счисления р. Тогда количество разрядов числа k = п/р, а общее количество чисел (N), которые могут быть составлены, равно:
Слайд 9Для нахождения положения максимума нужно найти производную функции N(p), приравнять ее
Приравнивая полученное выражение к нулю, получаем ln p = 1, или рт = е, где е = 2,71828... - основание натурального логарифма. Ближайшее к е целое число, очевидно, 3 - по этой причине троичная система счисления оказывается самой экономичной для представления чисел.
Слайд 10Перевод чисел между системами счисления 2 ↔ 8 ↔ 16
Двоичная система
Восьмеричная система счисления имеет основание 8 и цифры 0, 1.....7.
Шестнадцатеричная система счисления имеет основание 16 и цифры 0, 1, ..., 9, А, В, С, D, Е, F. При этом знак «А» является 16-ричной цифрой, соответствующей числу 10 в десятичной системе; В16 = 1110; С16 = 1210; D16 = 1310; Е16 = 1410; F16 = 1510. Другими словами, в данном случае А ... F - это не буквы латинского алфавита, а цифры 16-ричной системы счисления и поэтому они имеют только такое начертание (не могут быть представлены в виде, например, соответствующих строчных букв, как в текстах).
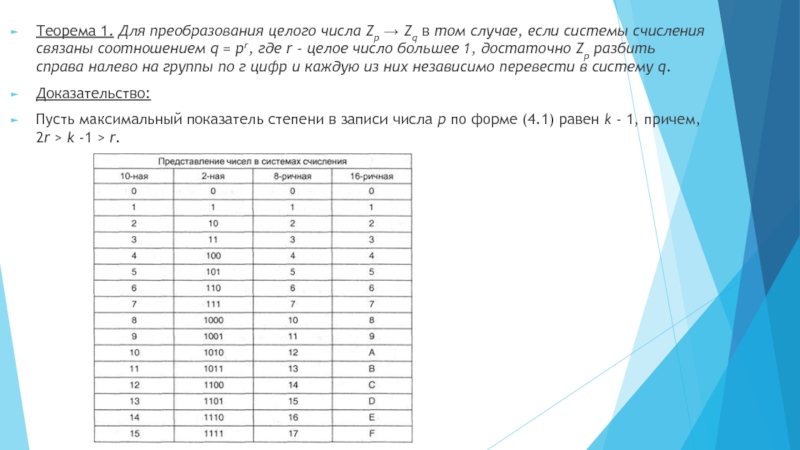
Слайд 11Теорема 1. Для преобразования целого числа Zp → Zq в том
Доказательство:
Пусть максимальный показатель степени в записи числа р по форме (4.1) равен k - 1, причем, 2r > k -1 > r.
Слайд 12Вынесем множитель рr из всех слагаемых, у которых j ≥ r.
Где:
Таким образом, r-разрядные числа системы с основанием р оказываются записанными как цифры системы с основанием q. Этот результат можно обобщить на ситуацию произвольного k-1 > r - в этом случае выделится не две, а больше (т) цифр числа с основанием q. Очевидно, Zq = (bm … b0 )q.
Слайд 13Теорема 2. Для преобразования целого числа Zp → Zq в том
Для каждой цифры справедливо: 0 ≤ ai ≤ р - 1 и поскольку р = qr, 0 ≤ ai ≤ qr-1, то в представлении этих цифр в системе счисления q максимальная степень многочленов (4.1) будет не более r - 1 и эти многочлены будут содержать по r цифр:
Тогда
причем, число Zq содержит 2r цифр. Доказательство легко обобщается на случай произвольного количества цифр в числе Zp.
Слайд 14Преобразование нормализованных чисел
Вещественное число X может быть представлено в двух формах
Число Х10 называется нормализованным, если оно представлено в виде Х10 = ± M10 ∙ 10±k10.
В этой записи М10 называется мантиссой нормализованного числа; значения мантиссы лежат в интервале 0,1 ≤ М10 ≤ 1. k10 называется порядком нормализованного числа - это целое положительное десятичное число
Аналогично нормализации десятичного числа можно в нормализованной форме представить и число в произвольной системе счисления р:
При этом значения мантиссы лежат в интервале р-1 ≤ Мр < 1 (т.е. первая значащая цифра мантиссы всегда ненулевая), а показатель степени представляется в системе р (kp). Например, для р = 2:
Мантисса располагается в промежутке 0,12 ≤ М2 < 1, что соответствует десятичному интервалу 0,510 ≤ M10 < 1.
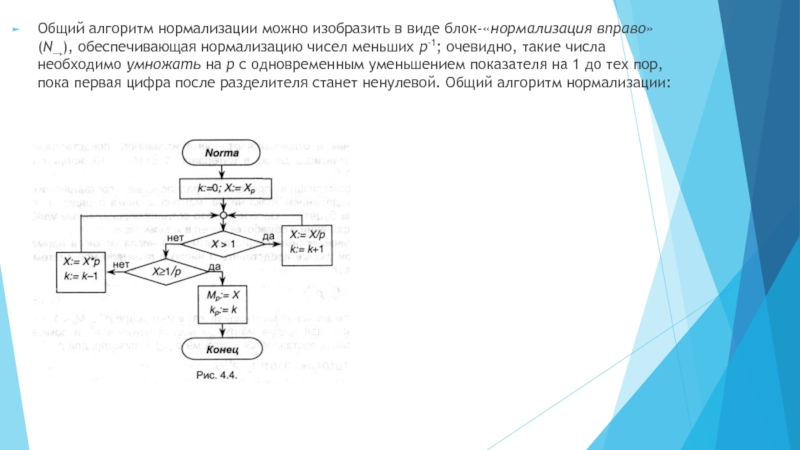
Слайд 15Общий алгоритм нормализации можно изобразить в виде блок-«нормализация вправо» (N→), обеспечивающая
Слайд 16
Пусть, имеется число Хр = ±Мр ∙ р±kp для которого необходимо
Из (4.13) вытекает, что для осуществления преобразования можно Мр умножить на рkp , т.е. перейти к естественной форме числа в системе р, перевести его в систему q, а затем нормализовать.
Слайд 17Различаются также ситуации kp ≥ 0 и kp < 0 -
Слайд 18Кодирование чисел в компьютере
и действия над ними
Методы кодировки и допустимые над
целые положительные числа (целые числа без знака);
целые числа со знаком;
вещественные нормализованные числа.
Слайд 19Кодирование и обработка в компьютере
целых чисел без знака
Будем исходить из
Для представления числа в регистре арифметико-логического устройства процессора, где формируется результат операции, имеется еще один дополнительный одноразрядный регистр, который называется регистром переноса и который можно рассматривать в качестве продолжения (т.е. 17-го бита) регистра результата.
Слайд 20Сложение производится согласно таблице сложения, которая для двоичных чисел имеет вид:
В последнем случае в том разряде, где находились слагаемые, оказывается 0, а 1 переносится в старший разряд. Место, где сохраняется переносимая в старший разряд 1 до того, как она будет использована в операции, называется битом переноса.
Умножение производится согласно таблице умножения, которая для двоичных чисел имеет предельно простой вид:
0 · 0 = 0
0 · 1 = 0
1 · 0 = 0
1 · 1 = 1
Слайд 21Кодирование и обработка в компьютере
целых чисел со знаком
Кодирование целых чисел, имеющих
Zmax = 215 - 1 = 3276710. Такое представление чисел называется прямым кодом.
Альтернативным вариантом является представление чисел со знаком в дополнительном коде.
Дополнением (D) k-разрядного целого числа Z в системе счисления р называется величина D(ZP, k) = pk - Z.
Данную формулу можно представить в ином виде: D(ZP, k) = ((pk - 1) - Z) + 1. Число pk - 1 согласно (4.8), состоит из k наибольших в данной системе счисления цифр (р - 1), например, 999910, FFF16 или 11111112. Поэтому (pk - 1) - Z можно получить путем дополнения до р-1 каждой цифры числа Z и последующим прибавлением к последнему разряду 1.
Слайд 22Кодирование и обработка в компьютере
вещественных чисел
Вещественные числа в компьютере заменяются их
Следствие 1 состоит в том, что строгие отношения между числами континуума превращаются в нестрогие для их компьютерных представителей, т.е.
Слайд 23Следствие 2. Поскольку код вещественного числа в компьютере является приблизительным представителем
Следствие 3. Наряду с понятием наибольшего вещественного числа (из-за ограниченности разрядной сетки) появляется понятие наименьшего числа или машинного нуля. Например, в типе Real языка PASCAL любое десятичное число, по модулю меньшее 2,3∙10-39 оказывается машинным нулем, т.е. считается равным 0 при сохранении и в операциях с ним. Таким образом, математическое понятие «0» как точное значение числа в компьютерном представлении заменяется понятием «машинный нуль» как значение числа меньшее некоторой определенной величины.
Как уже было сказано, основной формой представления кодов вещественных чисел в компьютере является двоичная нормализованная. При этом записываться и храниться в памяти компьютера должны все составляющие нормализованной формы , что требует нескольких ячеек памяти.
Поскольку значение мантиссы лежит в интервале 0,12 ≤ М2 < 1, ноль в разряде целых и разделитель десятичных разрядов в представление не включается, т.е. мантисса содержит только цифры дробной части.
Слайд 24Сложение нормализованных чисел
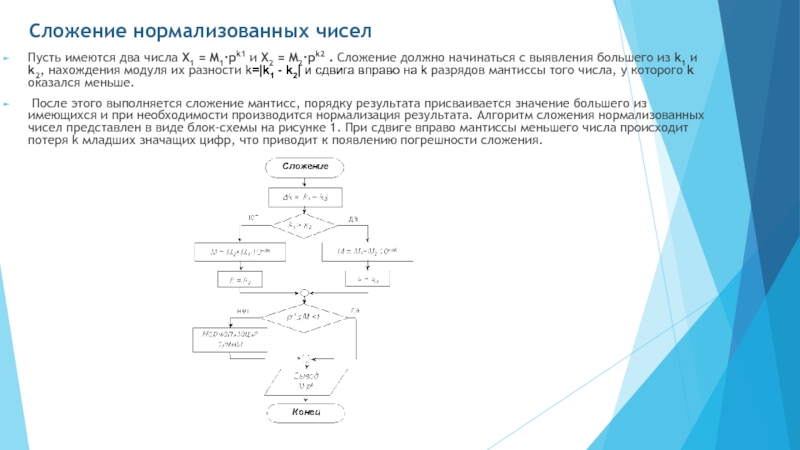
Пусть имеются два числа X1 = M1·pk1 и X2
После этого выполняется сложение мантисс, порядку результата присваивается значение большего из имеющихся и при необходимости производится нормализация результата. Алгоритм сложения нормализованных чисел представлен в виде блок-схемы на рисунке 1. При сдвиге вправо мантиссы меньшего числа происходит потеря k младших значащих цифр, что приводит к появлению погрешности сложения.
Слайд 25Умножение нормализованных чисел X1+X2 производится в соответствии с правилами: если по-прежнему
Операция деления, проводимая как над целыми, так и вещественными числами, приводит в общем случае к появлению вещественного числа, поэтому целые числа предварительно преобразуются в вещественный тип, т.е. переводятся в нормализованную форму.
Очевидно, при делении X1/X2 мантисса частного M = M1/M2, а порядок k = k1-k2. При этом непосредственно операция деления сводится к сдвигу делителя вправо и последовательному вычитанию его из делителя (т.е. сложения с дополнительным кодом вычитаемого). Как и в предыдущих операциях, результат деления при необходимости нормализуется.
Слайд 26Общие замечания.
1)В компьютерах арифметические устройства выполняют действия не с самими
2)Причиной отличий правил арифметики двоичных кодов от правил обычной арифметики является ограниченность разрядной сетки, применяемой для записи чисел в компьютере. По этой же причине отличаются понятия "нуль" и "машинный ноль", "бесконечность" – "максимальное число", а также становится возможной ситуация переполнения, что требует ее постоянного отслеживания.
3)Применение при вычислениях формы представления чисел с плавающей запятой обеспечивает единообразие при их записи и обработке, и, что важно, в результате автоматического масштабирования числа на каждом этапе его обработки сокращается погрешность вычислений.
4)Различие правил обработки целых и нормализованных чисел приводит к необходимости точного описания типов переменных перед их использованием в программах. Вторая причина описания типов состоит в оптимизации расходования памяти компьютера, поскольку числа разных типов требуют для хранения различных ресурсов памяти.