- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности. Непрерывные и дискретные поверхности презентация
Содержание
- 1. Поверхности. Непрерывные и дискретные поверхности
- 2. Непрерывные и дискретные поверхности Дискретные данные Изображение
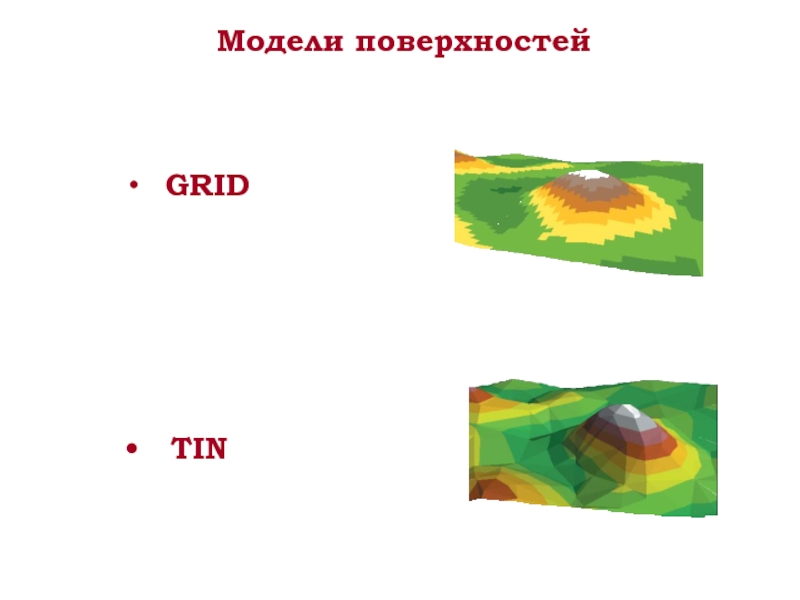
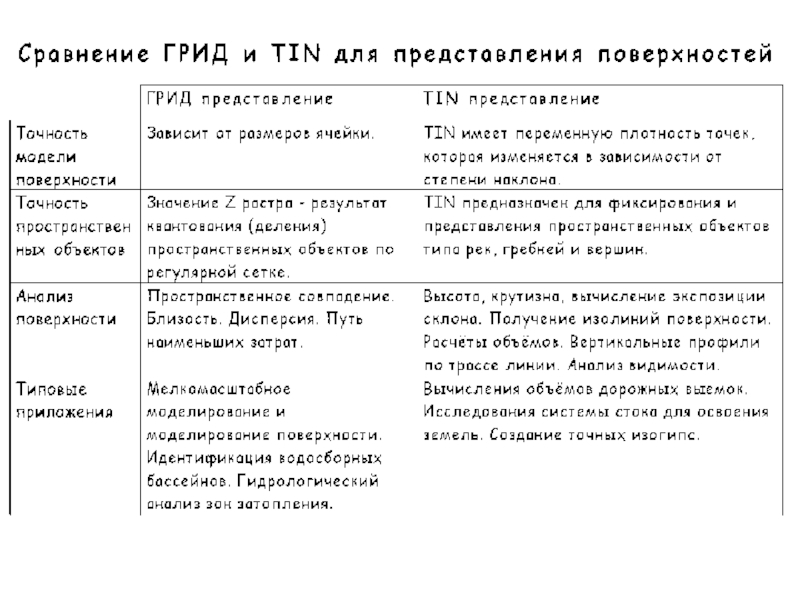
- 3. Модели поверхностей GRID TIN
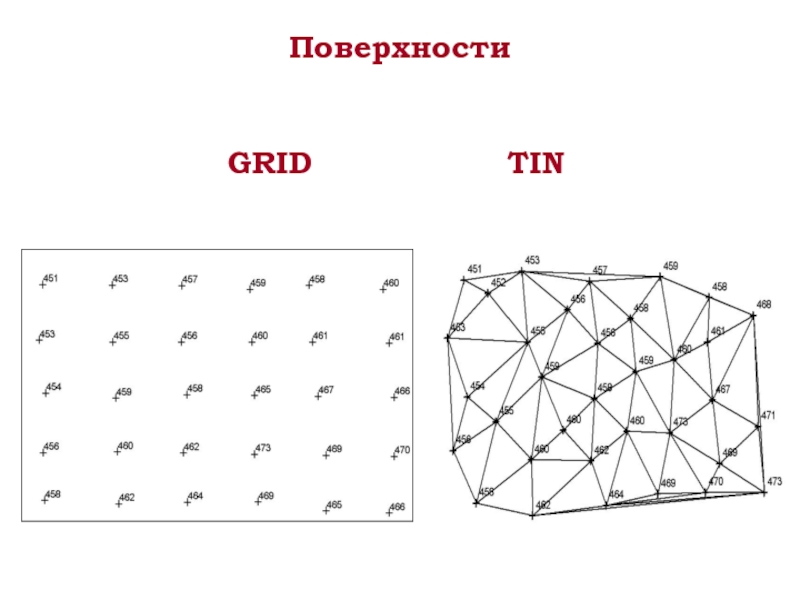
- 4. Поверхности GRID TIN
- 5. TIN - нерегулярные сети треугольников
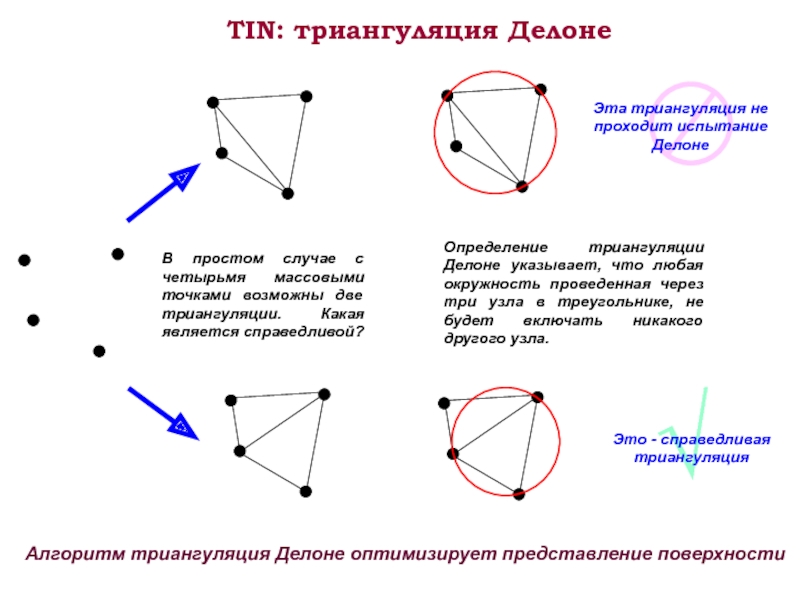
- 6. TIN: триангуляция Делоне Алгоритм триангуляция Делоне оптимизирует представление поверхности
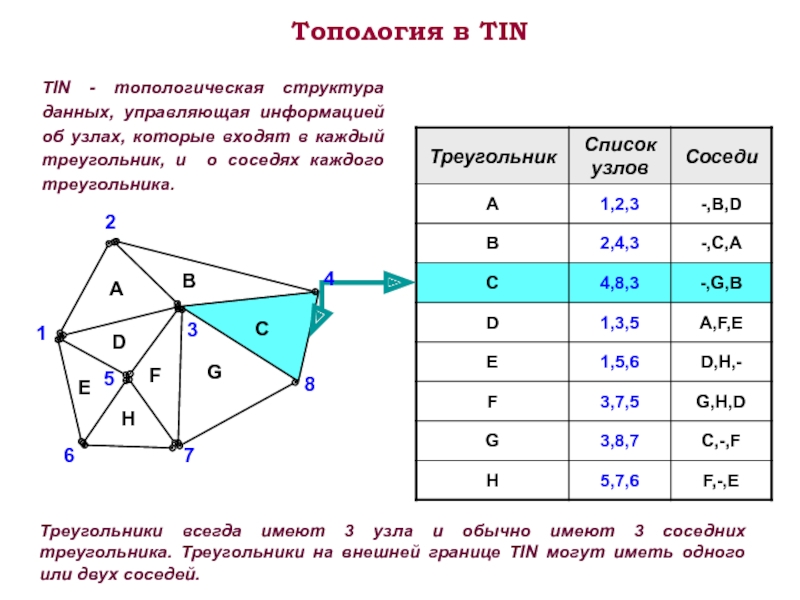
- 7. Топология в TIN TIN - топологическая структура
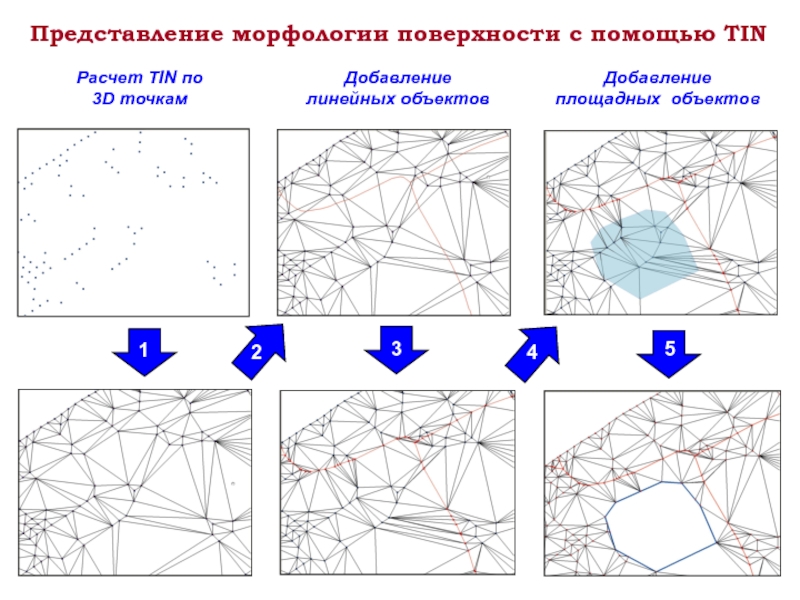
- 8. Представление морфологии поверхности с помощью TIN Расчет
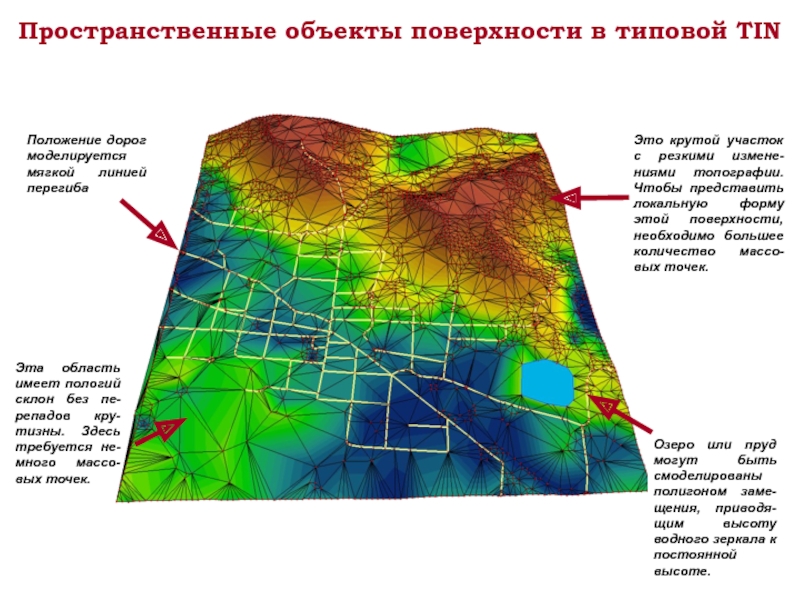
- 9. Пространственные объекты поверхности в типовой TIN Это
- 10. GRID - модель Гриды представляют поверхность по
- 12. Интерполяция Точечный набор известных значений Растр, интерполированный
- 13. Методы интерполяции Метод обратно взвешенных расстояний Сплайн Тренд Кригинг
- 14. Интерполяция: метод обратно взвешенных расстояний (IDW)
- 15. Метод обратно взвешенных расстояний (продолжение) интерполяция интерполяция с учетом барьеров
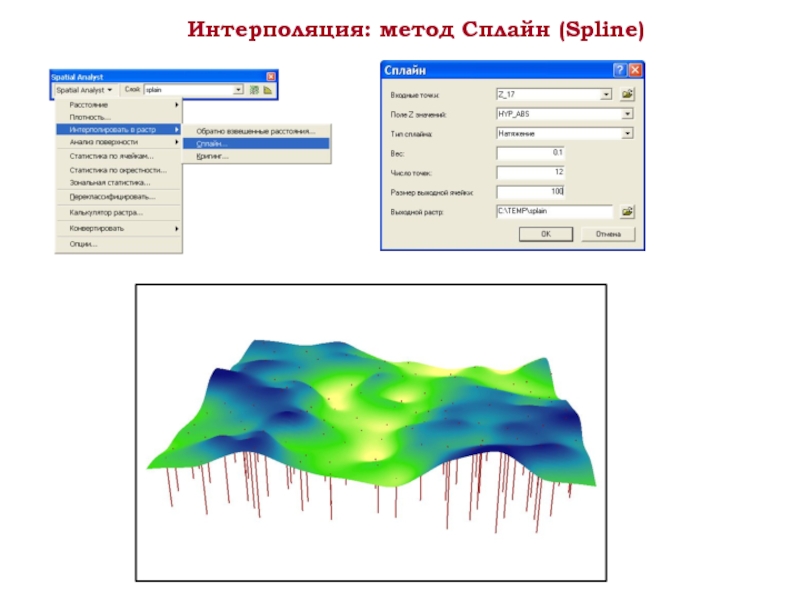
- 16. Интерполяция: метод Сплайн (Spline)
- 17. Интерполяция: метод Тренд (Trend) Аппроксимация поверхности тренда
- 18. Интерполяция: метод Кригинг Иллюстрация элементов кригинга. Дрейф
- 19. Метод Кригинг: вариограмма Образование пар точек:
- 20. Моделирование вариограммы Линейная модель Сферическая модель
- 21. Метод Кригинг: вычисление предполагаемых значений
- 22. Условия применения Кригинга Рельеф дна водохранилища, построенный
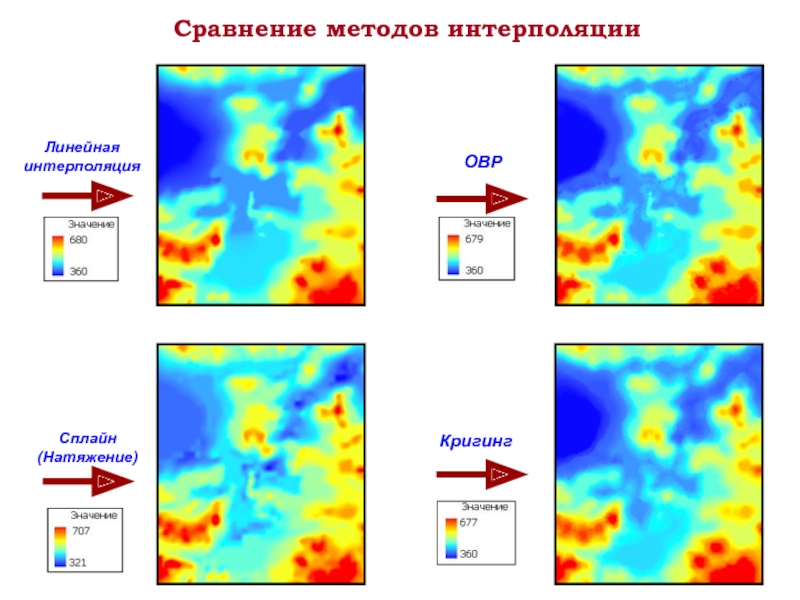
- 23. Сравнение методов интерполяции Линейная интерполяция ОВР Сплайн (Натяжение) Кригинг
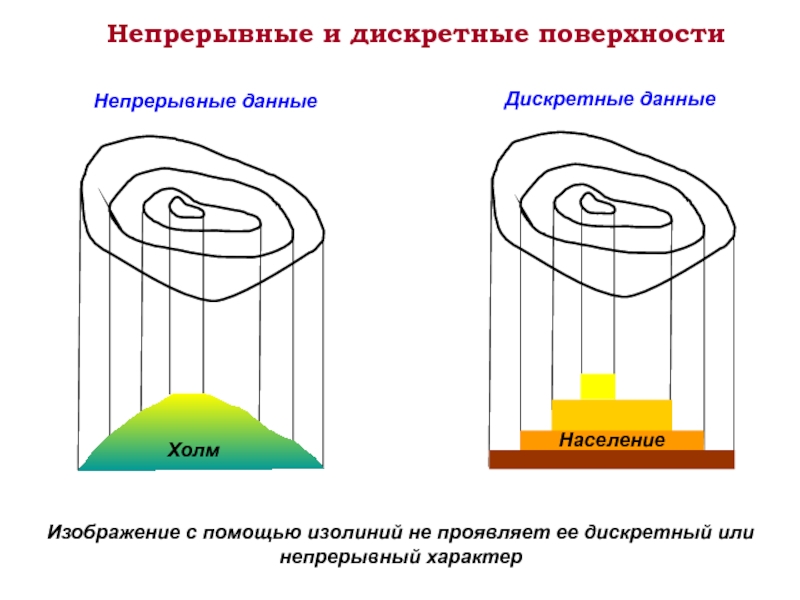
Слайд 2Непрерывные и дискретные поверхности
Дискретные данные
Изображение с помощью изолиний не проявляет ее
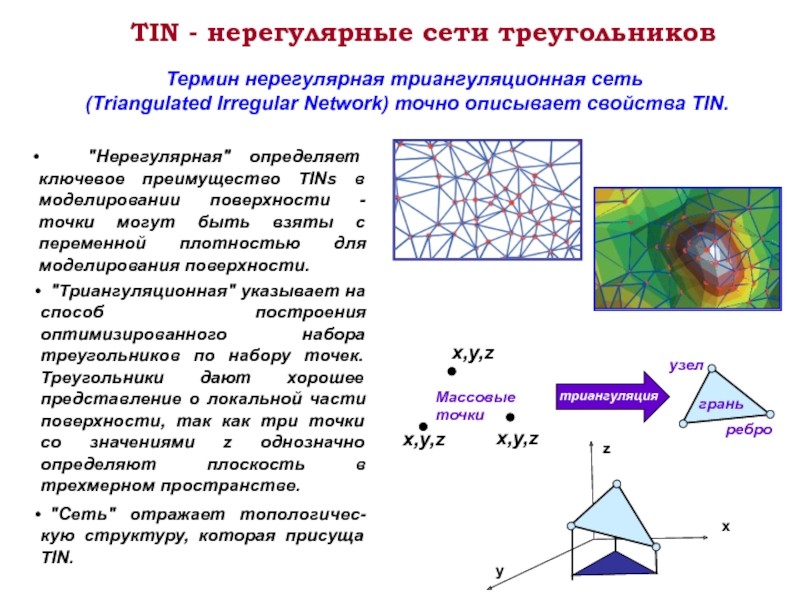
Слайд 5TIN - нерегулярные сети треугольников
"Нерегулярная" определяет ключевое преимущество TINs
Термин нерегулярная триангуляционная сеть
(Triangulated Irregular Network) точно описывает свойства TIN.
"Триангуляционная" указывает на способ построения оптимизированного набора треугольников по набору точек. Треугольники дают хорошее представление о локальной части поверхности, так как три точки со значениями z однозначно определяют плоскость в трехмерном пространстве.
"Сеть" отражает топологичес-кую структуру, которая присуща TIN.
x,y,z
x,y,z
x,y,z
Массовые точки
узел
ребро
грань
Слайд 7Топология в TIN
TIN - топологическая структура данных, управляющая информацией об узлах,
A
B
C
D
E
H
F
G
1
2
3
4
5
6
7
8
Треугольники всегда имеют 3 узла и обычно имеют 3 соседних треугольника. Треугольники на внешней границе TIN могут иметь одного или двух соседей.
Слайд 8Представление морфологии поверхности с помощью TIN
Расчет TIN по 3D точкам
Добавление линейных
Добавление площадных объектов
Слайд 9Пространственные объекты поверхности в типовой TIN
Это крутой участок с резкими измене-ниями
Эта область имеет пологий склон без пе-репадов кру-тизны. Здесь требуется не-много массо-вых точек.
Озеро или пруд могут быть смоделированы полигоном заме-щения, приводя-щим высоту водного зеркала к постоянной высоте.
Положение дорог моделируется мягкой линией перегиба
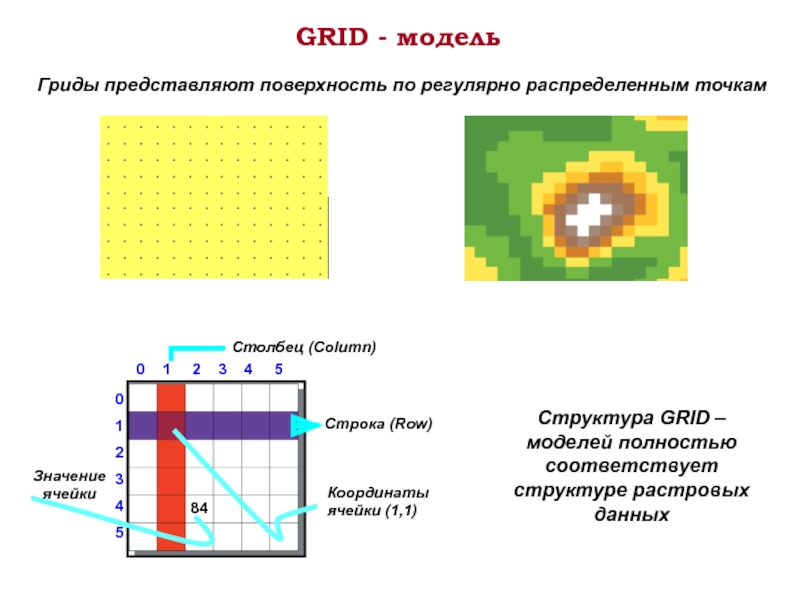
Слайд 10GRID - модель
Гриды представляют поверхность по регулярно распределенным точкам
Строка (Row)
Столбец
0 1 2 3 4 5
0
1
2
3
4
5
Координаты ячейки (1,1)
Значение ячейки
Структура GRID – моделей полностью соответствует структуре растровых данных
Слайд 12Интерполяция
Точечный набор известных
значений
Растр, интерполированный по точкам.
Ячейки, выделенные красным,
указывают точки исходного набора.
Интерполяция
интерполяция
High
Low
интерполяция
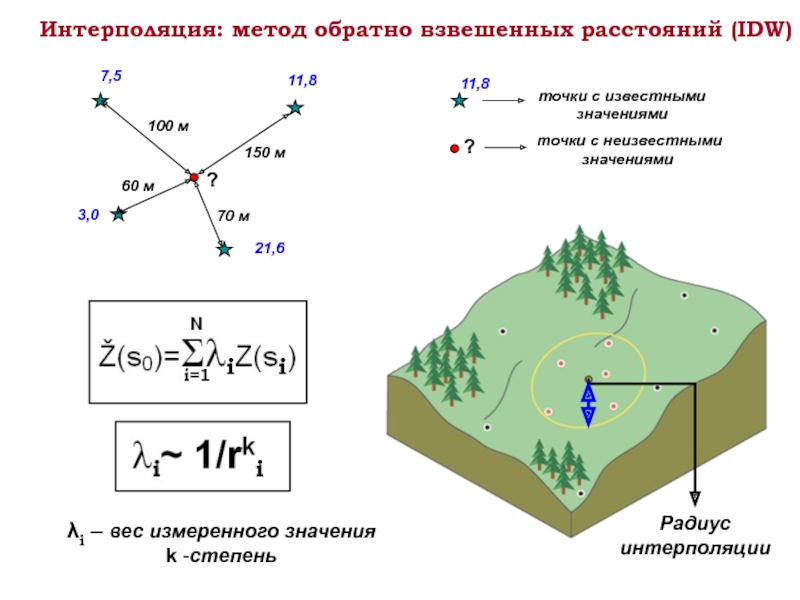
Слайд 14Интерполяция: метод обратно взвешенных расстояний (IDW)
λi – вес измеренного значения
k -степень
Радиус
11,8
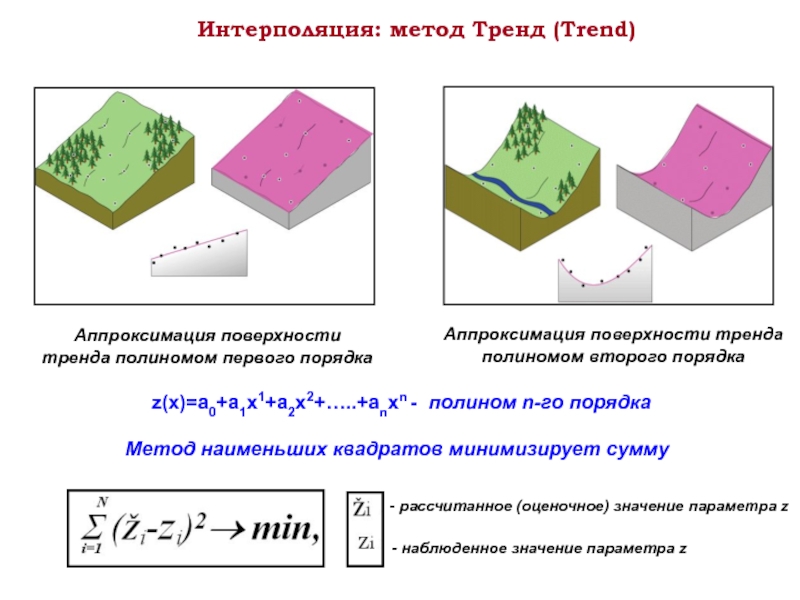
Слайд 17Интерполяция: метод Тренд (Trend)
Аппроксимация поверхности тренда полиномом первого порядка
Аппроксимация поверхности тренда
z(х)=a0+a1x1+a2x2+…..+anxn - полином n-го порядка
Метод наименьших квадратов минимизирует сумму
- рассчитанное (оценочное) значение параметра z
- наблюденное значение параметра z
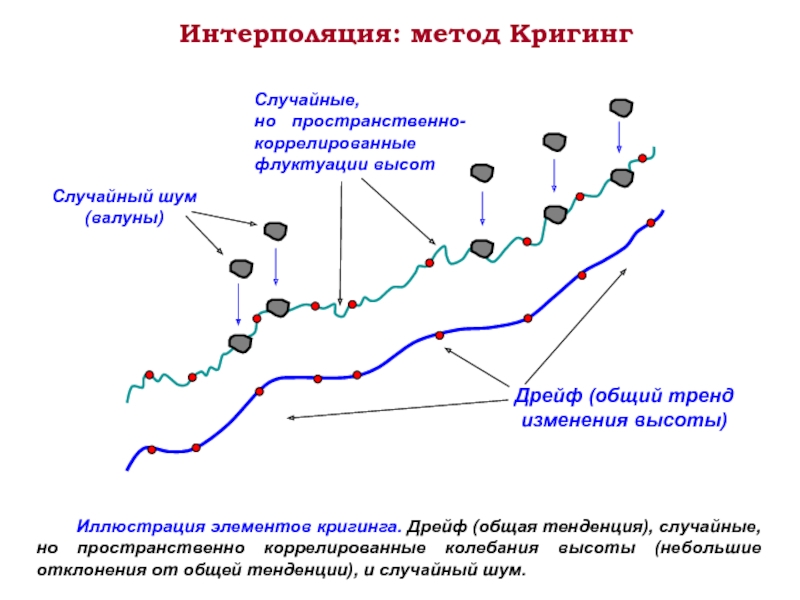
Слайд 18Интерполяция: метод Кригинг
Иллюстрация элементов кригинга. Дрейф (общая тенденция), случайные, но пространственно
Дрейф (общий тренд изменения высоты)
Случайные,
но пространственно- коррелированные флуктуации высот
Случайный шум (валуны)
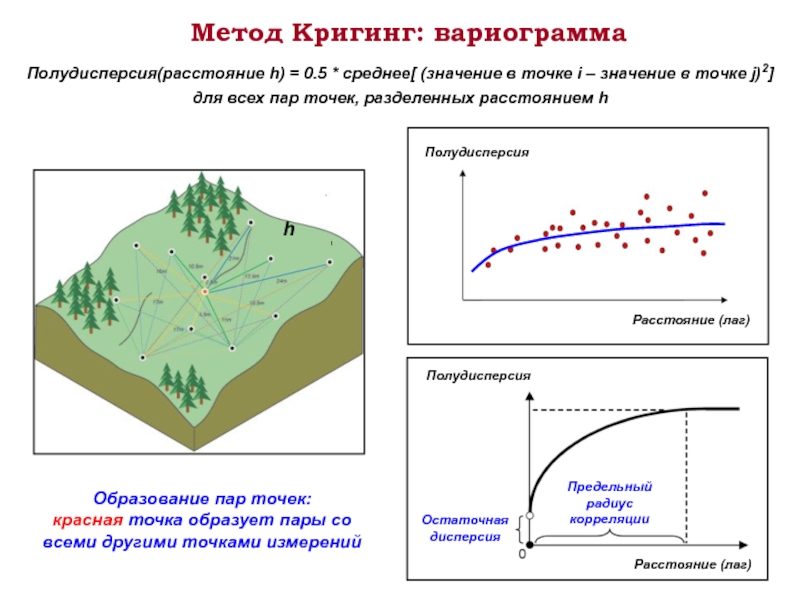
Слайд 19Метод Кригинг: вариограмма
Образование пар точек:
красная точка образует пары со всеми
Полудисперсия(расстояние h) = 0.5 * среднее[ (значение в точке i – значение в точке j)2]
для всех пар точек, разделенных расстоянием h
h
Полудисперсия
Расстояние (лаг)
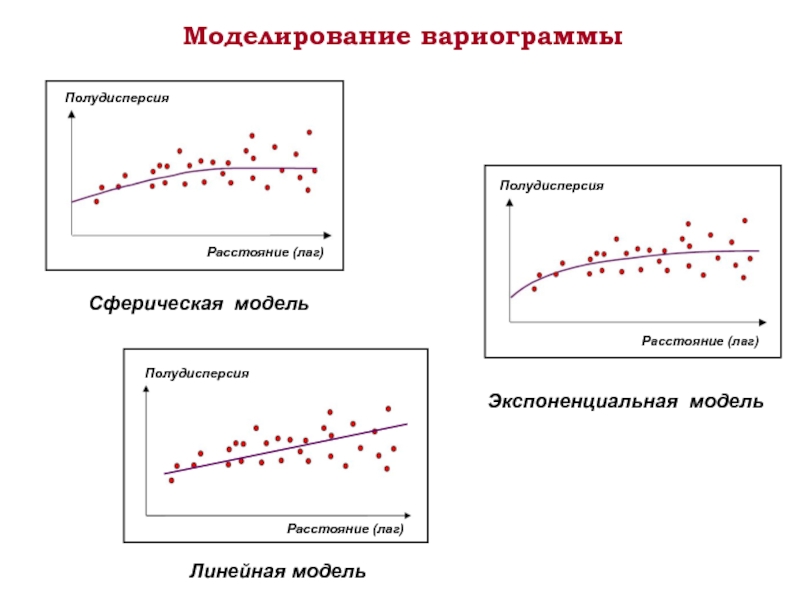
Слайд 20Моделирование вариограммы
Линейная модель
Сферическая модель
Экспоненциальная модель
Полудисперсия
Расстояние (лаг)
Полудисперсия
Расстояние (лаг)
Полудисперсия
Расстояние (лаг)
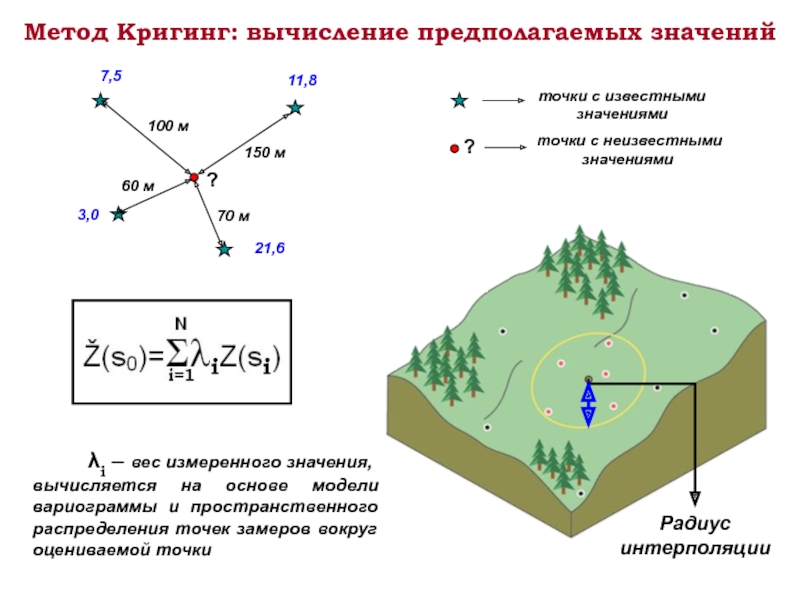
Слайд 21Метод Кригинг: вычисление предполагаемых значений
λi –
вычисляется на основе модели вариограммы и пространственного распределения точек замеров вокруг оцениваемой точки
Радиус интерполяции
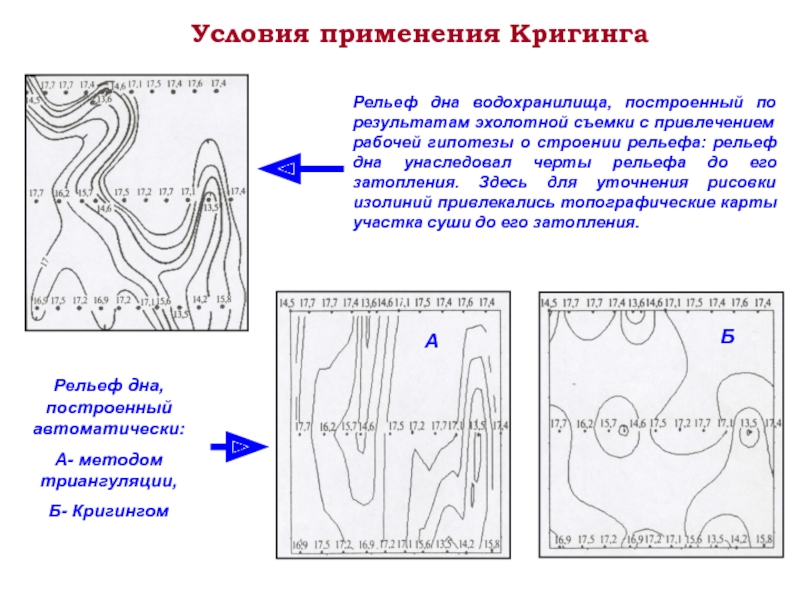
Слайд 22Условия применения Кригинга
Рельеф дна водохранилища, построенный по результатам эхолотной съемки с
Рельеф дна, построенный автоматически:
А- методом триангуляции,
Б- Кригингом
А
Б