- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Помехоустойчивое кодирование. Декодирование циклических кодов презентация
Содержание
- 1. Помехоустойчивое кодирование. Декодирование циклических кодов
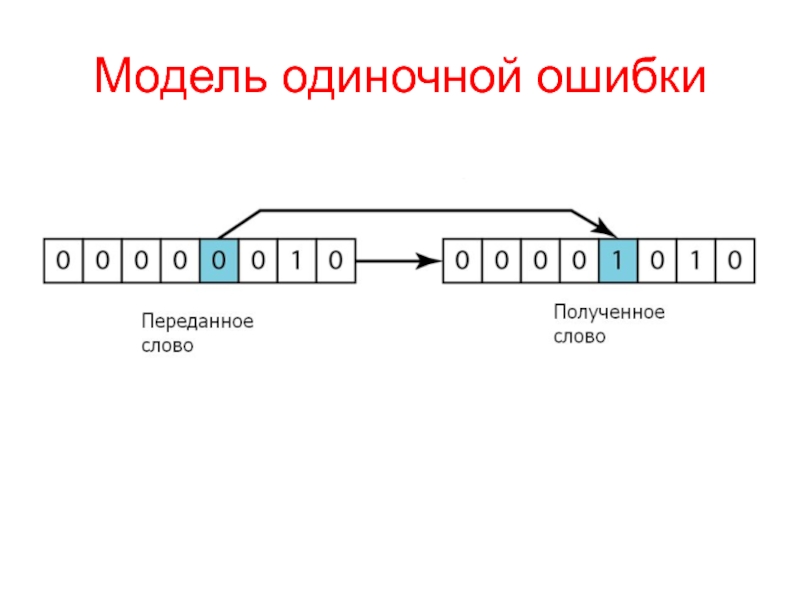
- 2. Модель одиночной ошибки
- 3. Модель ошибки Пусть c(x) – передаваемый по каналу многочлен. Тогда полученный ошибочный многочлен
- 4. Модель ошибки Если e(x)=0, то полученный многочлен
- 5. Связь между многочленом ошибок и синдромом
- 6. Связь между многочленом ошибок и синдромом
- 7. Связь между многочленом ошибок и синдромом Синдром
- 8. Свойства синдрома циклического кода Теорема (Меггитт). Пусть
- 9. Алгоритм Меггитта Получаем остаток от деления е(х),
Модель одиночной ошибки
Слайд 3Модель ошибки
Пусть c(x) – передаваемый по каналу многочлен.
Тогда полученный ошибочный многочлен
Слайд 4Модель ошибки
Если e(x)=0, то полученный многочлен без остатка делится на порождающий
многочлен.
В противном случае
В противном случае
Слайд 7Связь между многочленом ошибок и синдромом
Синдром принятого многочлена равен остатку от
деления многочлена ошибки на порождающий многочлен.
Слайд 8Свойства синдрома циклического кода
Теорема (Меггитт). Пусть -
синдром принятого из канала многочлена Обозначим синдром циклического сдвига принятого многочлена . Тогда
Слайд 9Алгоритм Меггитта
Получаем остаток от деления е(х), соответствующего ошибке в старшем разряде
[1000000000], на порождающий полином g(x):
Делим полученный полином c(х) на g(x) и получаем текущий остаток r(x).
Сравниваем
Если они равны, то ошибка произошла в старшем разряде.
Если нет, то увеличиваем степень принятого полинома на x и снова проводим деления: x·c(x) на g(x), остаток опять обозначим r(x)
Опять сравниваем полученный остаток с
Если они равны, то ошибки во втором по старшинству разряде.
Если нет, то берем х · х ·c(х) · и повторяем эти операции до тех пор, пока r(x) не будет равен
Делим полученный полином c(х) на g(x) и получаем текущий остаток r(x).
Сравниваем
Если они равны, то ошибка произошла в старшем разряде.
Если нет, то увеличиваем степень принятого полинома на x и снова проводим деления: x·c(x) на g(x), остаток опять обозначим r(x)
Опять сравниваем полученный остаток с
Если они равны, то ошибки во втором по старшинству разряде.
Если нет, то берем х · х ·c(х) · и повторяем эти операции до тех пор, пока r(x) не будет равен
