- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Планарные графы презентация
Содержание
- 1. Планарные графы
- 2. ГЕОГРАФИЧЕСКИЕ КАРТЫ Политическая
- 3. ТЕОРЕМА О ЧЕТЫРЕХ КРАСКАХ. Теорема (доказана
- 4. ТОР Теорема 2: Любую карту, нарисованную на
- 5. КРЕНДЕЛЬ Теорема 3: Любую карту, нарисованную на
- 6. ТОПОЛОГИЯ В топологии считается, что все тела
- 7. ОПРЕДЕЛЕНИЕ ПЛАНАРНОГО ГРАФА Граф, изображенный на плоскости
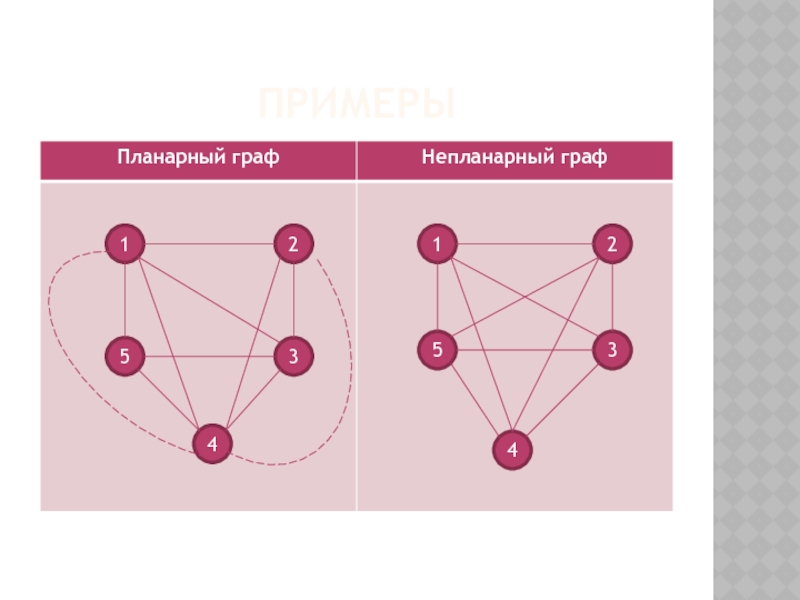
- 8. ПРИМЕРЫ 1 1 3 5 2 4 4 3 5 2
- 9. ЧТО ТАКОЕ «ГРАНЬ» Гранью (страной)
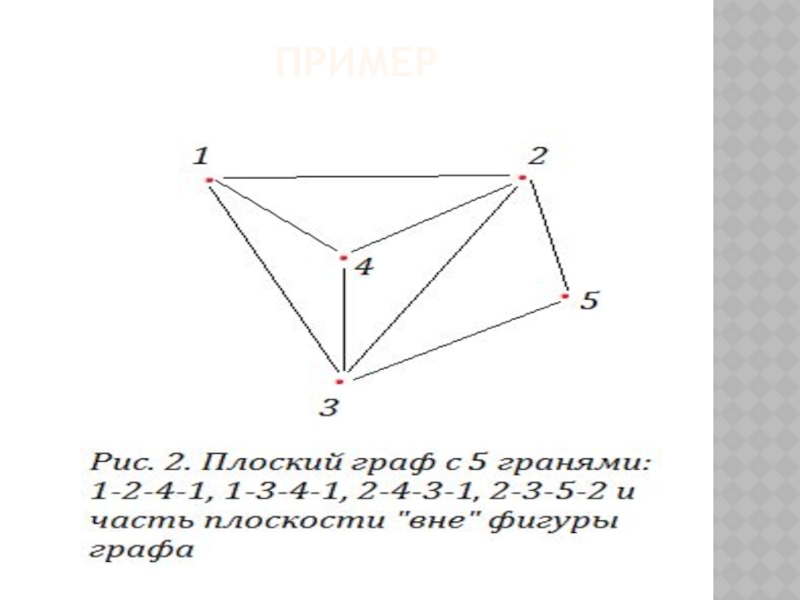
- 10. ПРИМЕР
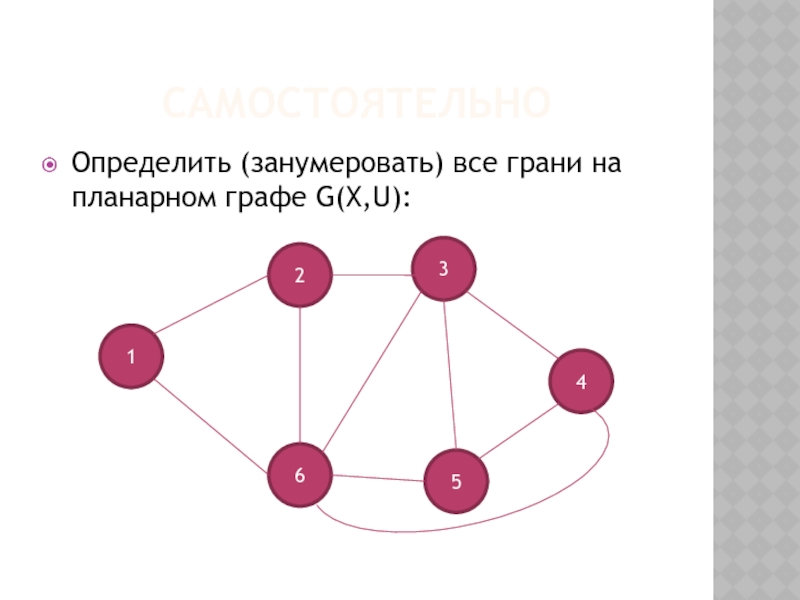
- 11. САМОСТОЯТЕЛЬНО Определить (занумеровать) все грани на планарном
- 12. ТЕОРЕМА ЭЙЛЕРА Пусть В - количество вершин
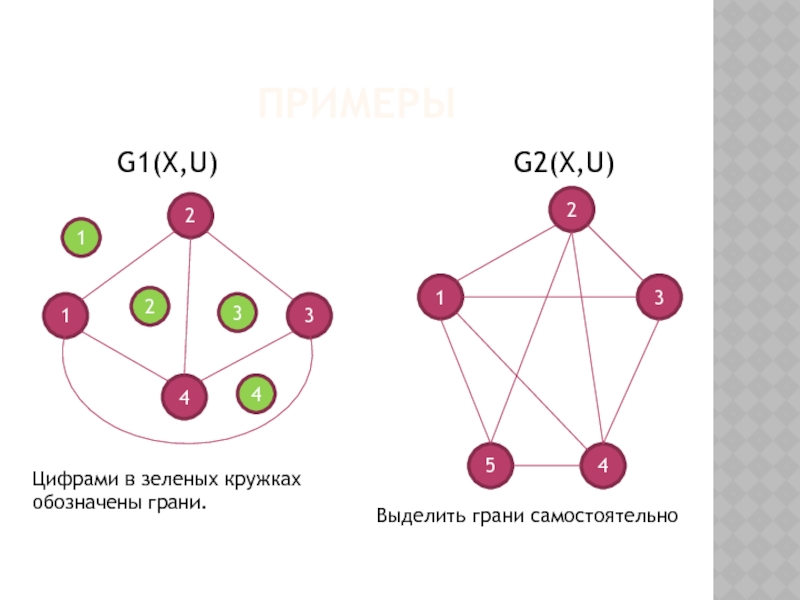
- 13. ПРИМЕРЫ G1(X,U)
- 14. ФОРМУЛА ЭЙЛЕРА ДЛЯ НЕСВЯЗНОГО ГРАФА
- 16. ТЕОРЕМА КУРАТОВСКОГО - ПОНТРЯГИНА Граф планарен
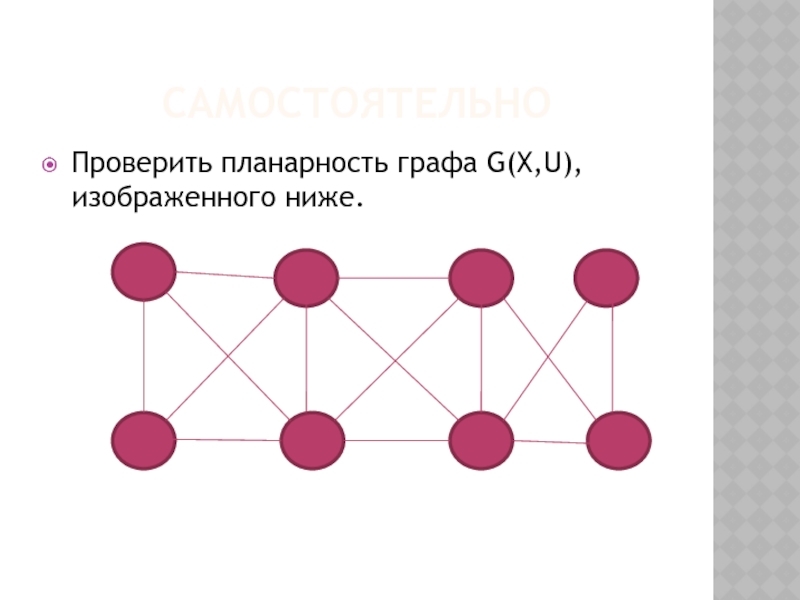
- 17. САМОСТОЯТЕЛЬНО Проверить планарность графа G(X,U), изображенного ниже.
- 18. ДВОЙСТВЕННЫЕ ГРАФЫ Правила построения двойственного графа: 1.
- 19. ПРАВИЛО ПРАВОЙ РУКИ Построение двойственной дуги: 4
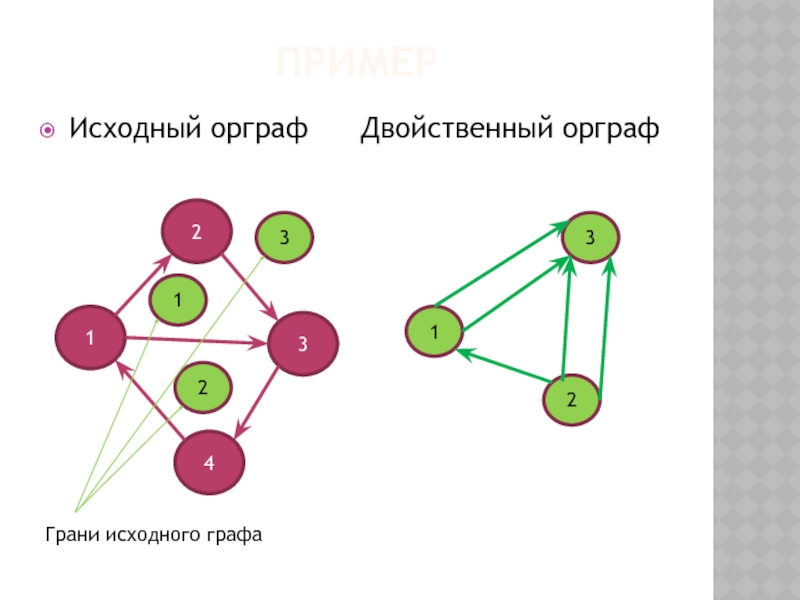
- 20. ПРИМЕР Исходный орграф Двойственный орграф
- 21. СВОЙСТВА ДВОЙСТВЕННЫХ ГРАФОВ Простому контуру исходного графа,
- 22. СЛЕДСТВИЕ ТЕОРЕМЫ 1 Вершины любого планарного графа
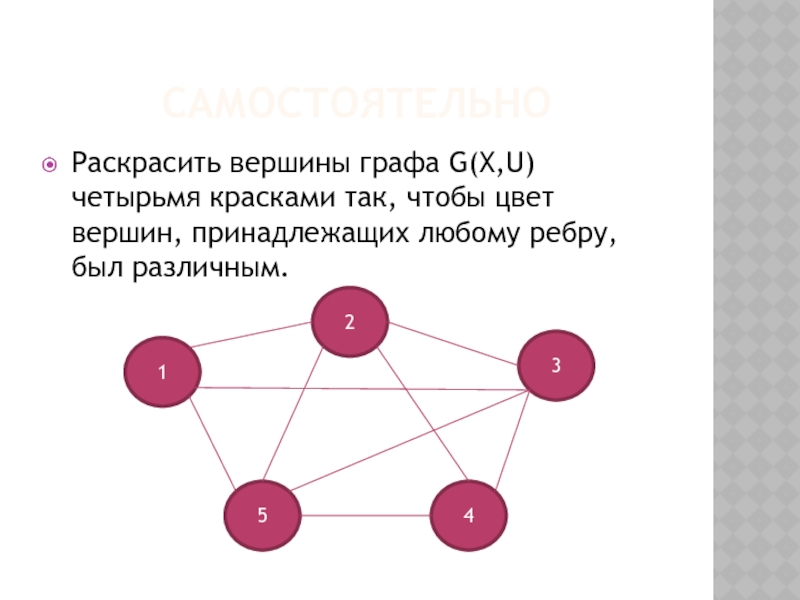
- 23. САМОСТОЯТЕЛЬНО Раскрасить вершины графа G(X,U) четырьмя красками
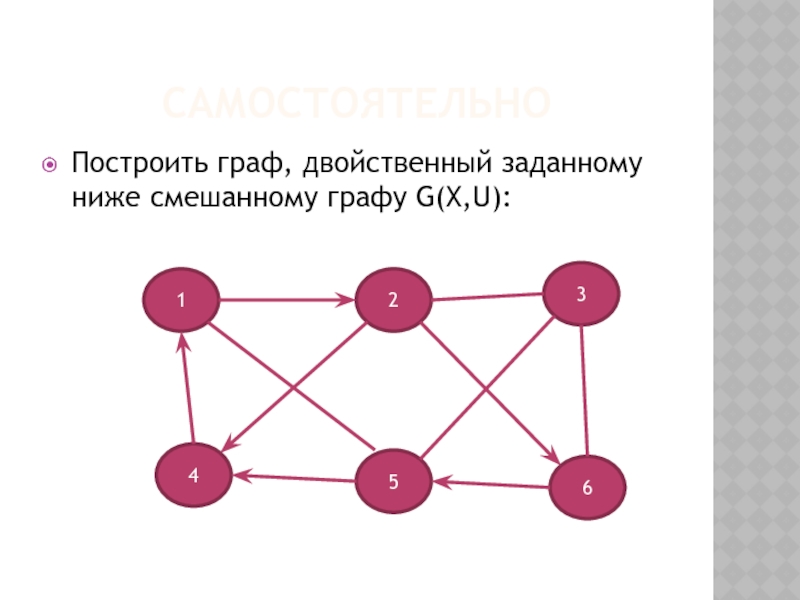
- 24. САМОСТОЯТЕЛЬНО Построить граф, двойственный заданному ниже смешанному графу G(X,U): 1 4 5 6 3 2
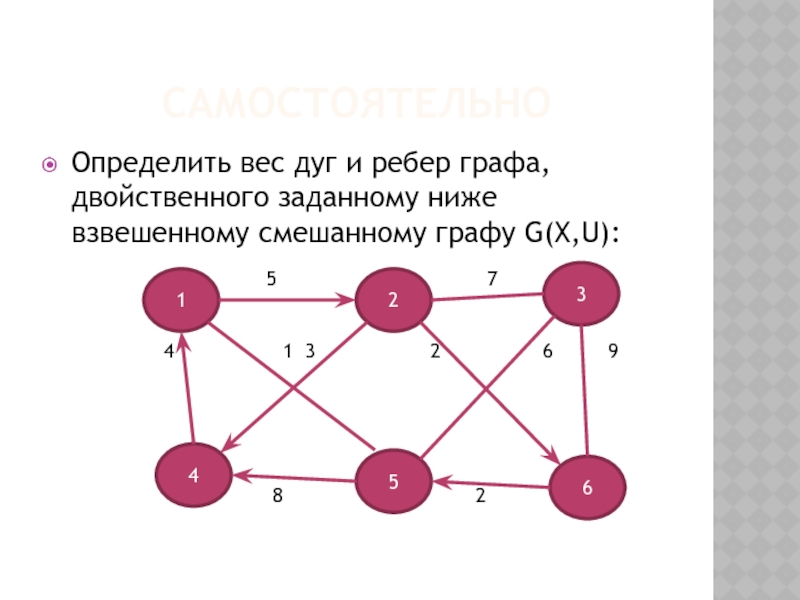
- 25. САМОСТОЯТЕЛЬНО Определить вес дуг и ребер графа,
- 26. САМОСТОЯТЕЛЬНО Для каких из этих тел справедлива теорема о четырех красках?
Слайд 2ГЕОГРАФИЧЕСКИЕ КАРТЫ
Политическая
карта карта
Толчком, ускорившим развитие теории графов, явилась эпоха великих географических открытий.
Слайд 3
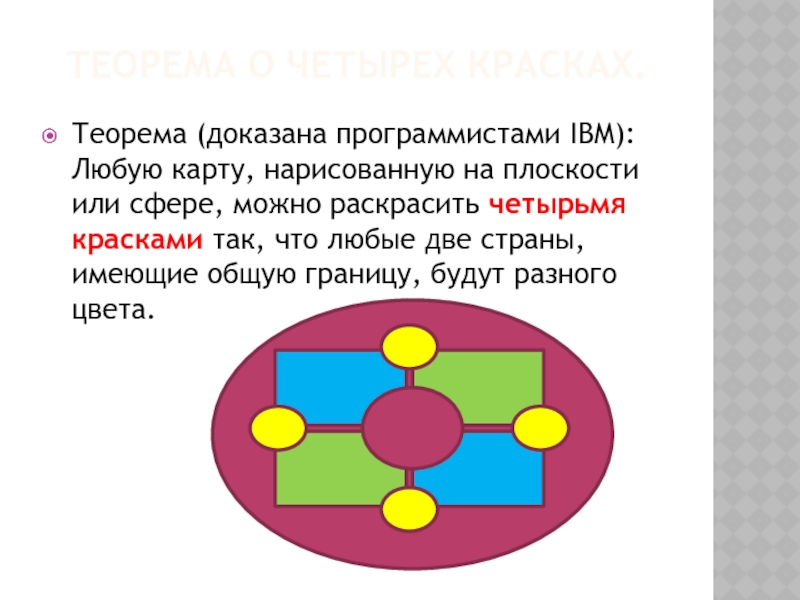
ТЕОРЕМА О ЧЕТЫРЕХ КРАСКАХ.
Теорема (доказана программистами IBM): Любую карту, нарисованную на
Слайд 4ТОР
Теорема 2: Любую карту, нарисованную на торе, можно раскрасить пятью красками
Слайд 5КРЕНДЕЛЬ
Теорема 3: Любую карту, нарисованную на поверхности кренделя, можно раскрасить шестью
Слайд 6ТОПОЛОГИЯ
В топологии считается, что все тела сделаны из эластичного материала, и
Т.о. топология изучает свойства гомеоморфных тел.
Слайд 7ОПРЕДЕЛЕНИЕ ПЛАНАРНОГО ГРАФА
Граф, изображенный на плоскости или на шаре, называется плоским
Слайд 9ЧТО ТАКОЕ «ГРАНЬ»
Гранью (страной) в плоском представлении графа называется
Слайд 12ТЕОРЕМА ЭЙЛЕРА
Пусть В - количество вершин в графе, Г - количество
В + Г - Р = 2
Слайд 13ПРИМЕРЫ
G1(X,U)
2
5
3
1
2
4
4
3
1
2
1
4
3
Цифрами в зеленых кружках
обозначены грани.
Выделить грани самостоятельно
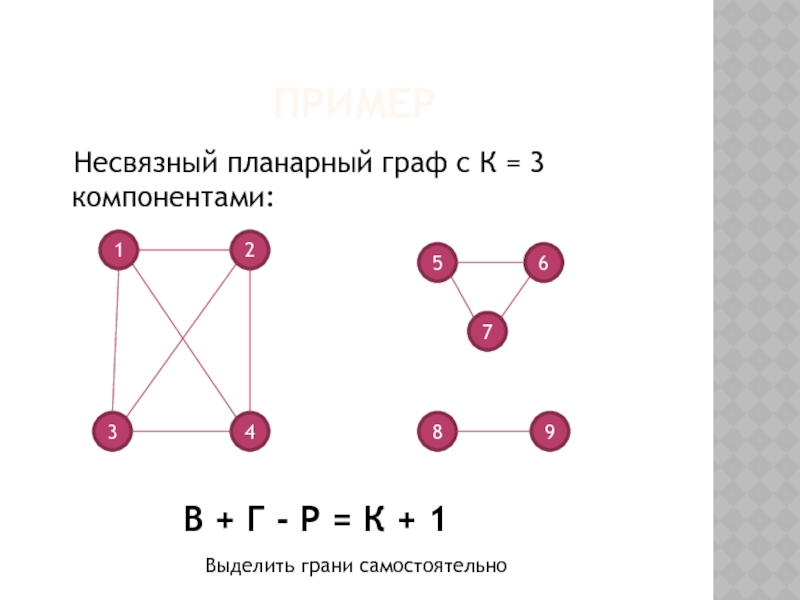
Слайд 14ФОРМУЛА ЭЙЛЕРА ДЛЯ НЕСВЯЗНОГО ГРАФА
Для несвязного планарного графа с
В + Г - Р = K + 1.
Слайд 15 ПРИМЕР
1
4
2
3
8
9
7
5
6
В + Г - Р = К + 1
Выделить грани самостоятельно
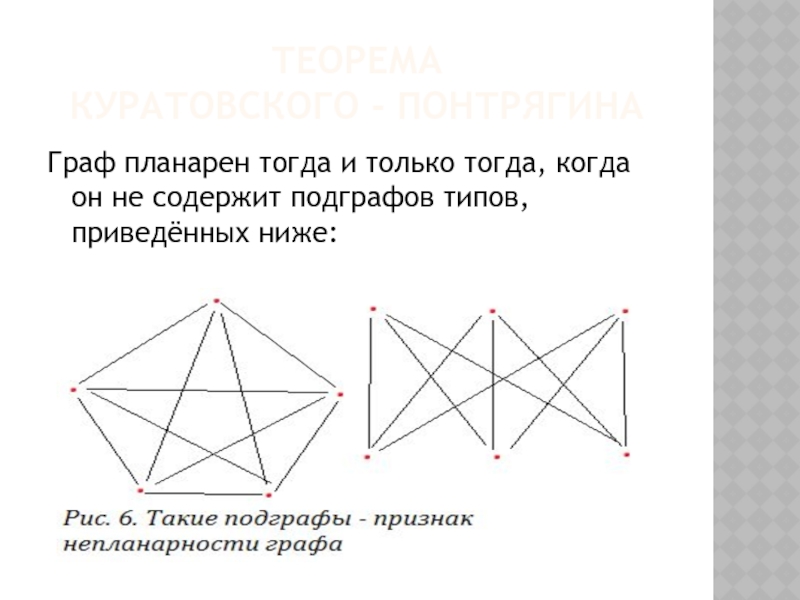
Слайд 16ТЕОРЕМА
КУРАТОВСКОГО - ПОНТРЯГИНА
Граф планарен тогда и только тогда, когда он
Слайд 18ДВОЙСТВЕННЫЕ ГРАФЫ
Правила построения двойственного графа:
1. Каждая грань исходного графа заменяется вершиной
Если граф неориентированный, то каждое ребро исходного графа заменяется пересекающим его ребром двойственного.
Если исходный граф ориентированный, то каждая дуга исходного графа заменяется пересекающей ее дугой двойственного графа по «правилу правой руки».
Если исходный граф является взвешенным, то вес каждого ребра (дуги) двойственного графа равен весу ребра (дуги), которую оно (она) пересекает.
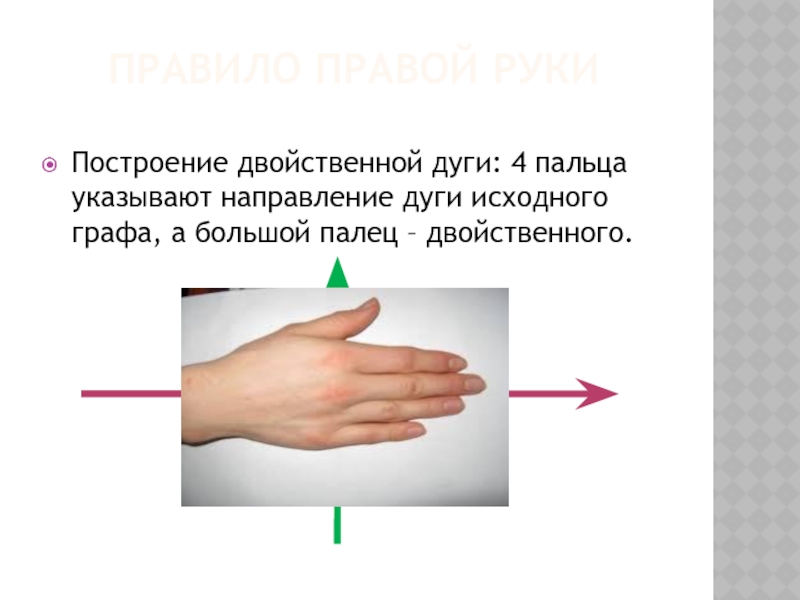
Слайд 19ПРАВИЛО ПРАВОЙ РУКИ
Построение двойственной дуги: 4 пальца указывают направление дуги исходного
Слайд 21СВОЙСТВА ДВОЙСТВЕННЫХ ГРАФОВ
Простому контуру исходного графа, «закрученному» по часовой стрелке, соответствует
Простому контуру исходного графа, «закрученному» против часовой стрелки, соответствует вершина-сток двойственного графа.
Грани исходного графа, образованной встречно ориентированными дугами, соответствует вершина двойственного графа, которой инцидентны, как заходящие, так и исходящие дуги.
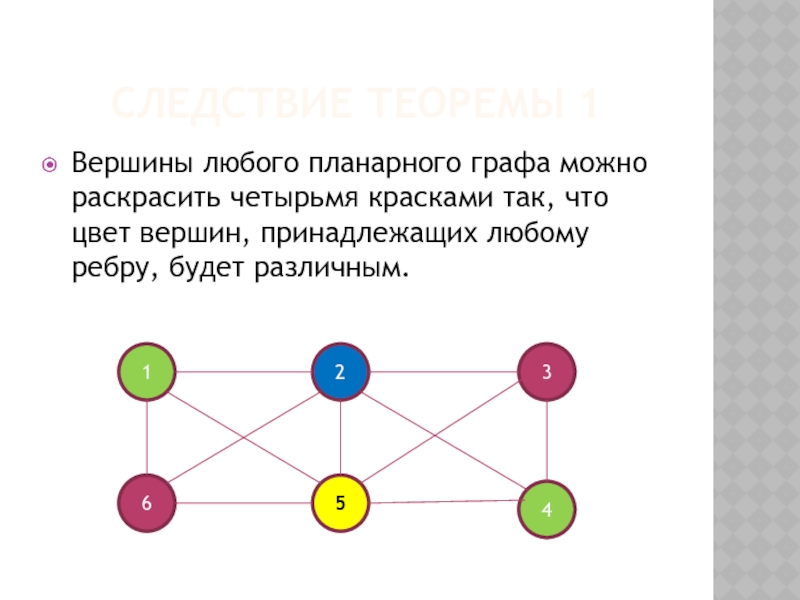
Слайд 22СЛЕДСТВИЕ ТЕОРЕМЫ 1
Вершины любого планарного графа можно раскрасить четырьмя красками так,
1
6
5
4
3
2
Слайд 23САМОСТОЯТЕЛЬНО
Раскрасить вершины графа G(X,U) четырьмя красками так, чтобы цвет вершин, принадлежащих
2
1
3
4
5
Слайд 25САМОСТОЯТЕЛЬНО
Определить вес дуг и ребер графа, двойственного заданному ниже взвешенному смешанному
1
4
5
6
3
2
5 7
4 1 3 2 6 9
8 2