- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Перевод чисел из одной системы счисления в другую презентация
Содержание
- 1. Перевод чисел из одной системы счисления в другую
- 2. Системы счисления Система
- 3. Основание системы счисления Запись
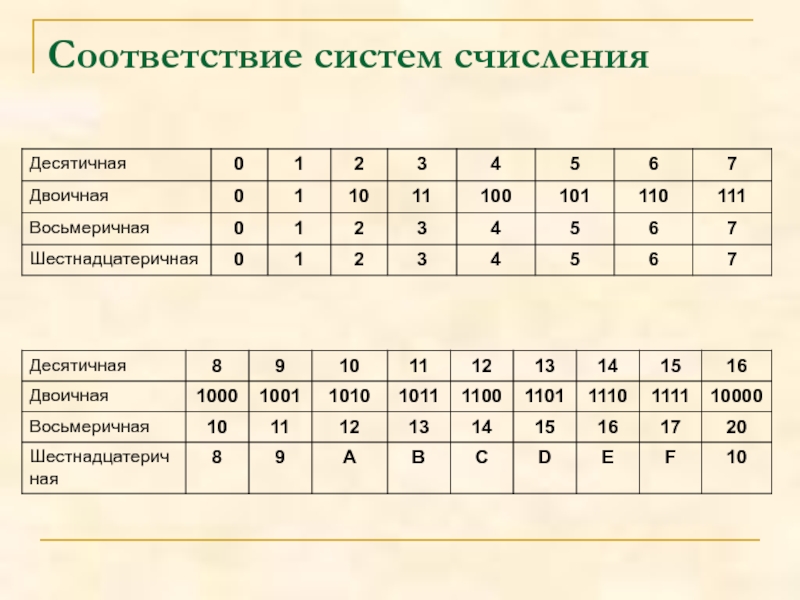
- 4. Соответствие систем счисления
- 5. Перевод целых чисел из десятичной системы
- 6. Перевод дробных чисел из десятичной системы счисления
- 7. Перевод чисел в десятичную систему счисления
- 8. Перевод из 8-ой и 16-ой системы счисления
- 9. Перевод из 2-ой системы счисления в
Слайд 2Системы счисления
Система счисления – это знаковая система,
в которой числа записываются по определенным правилам с помощью знаков некоторого алфавита, называемых цифрами.
Позиционные
Непозиционные
Системы
счисления
Слайд 3Основание системы счисления
Запись чисел в каждой из систем
счисления с основанием q означает сокращенную запись выражения
an-1qn-1 + an-2qn-2 + … + a1q1 + a0q0 + a-1q-1 + … + a-mq-m ,
где ai – цифры системы счисления, n и m –число целых и дробных разрядов соответственно
an-1qn-1 + an-2qn-2 + … + a1q1 + a0q0 + a-1q-1 + … + a-mq-m ,
где ai – цифры системы счисления, n и m –число целых и дробных разрядов соответственно
Слайд 5Перевод целых чисел из
десятичной системы счисления
Алгоритм перевода:
Последовательно делить с остатком
данное число и получаемые целые частные на основание новой системы счисления до тех пор, пока частное не станет равно нулю.
Полученные остатки выразить цифрами алфавита новой системы счисления
Записать число в новой системе счисления из полученных остатков, начиная с последнего.
Полученные остатки выразить цифрами алфавита новой системы счисления
Записать число в новой системе счисления из полученных остатков, начиная с последнего.
Слайд 6Перевод дробных чисел из десятичной системы счисления
Алгоритм перевода:
Последовательно умножать десятичную дробь
и получаемые дробные части произведений на основание новой системы счисления до тех пор, пока дробная часть не станет равна нулю или не будет достигнута необходимая точность перевода.
Полученные целые части произведений выразить цифрами алфавита новой системы счисления.
Записать дробную часть числа в новой системе счисления начиная с целой части первого произведения.
Полученные целые части произведений выразить цифрами алфавита новой системы счисления.
Записать дробную часть числа в новой системе счисления начиная с целой части первого произведения.
Слайд 7Перевод чисел в десятичную систему счисления
При переводе числа из
системы счисления с основанием q в десятичную
надо представить это число в виде суммы произведений степеней
основания его системы счисления q на соответствующие цифры числа.
an-1qn-1 + an-2qn-2 + … + a1q1 + a0q0 + a-1q-1 + … + a-mq-m
и выполнить арифметические вычисления.
надо представить это число в виде суммы произведений степеней
основания его системы счисления q на соответствующие цифры числа.
an-1qn-1 + an-2qn-2 + … + a1q1 + a0q0 + a-1q-1 + … + a-mq-m
и выполнить арифметические вычисления.
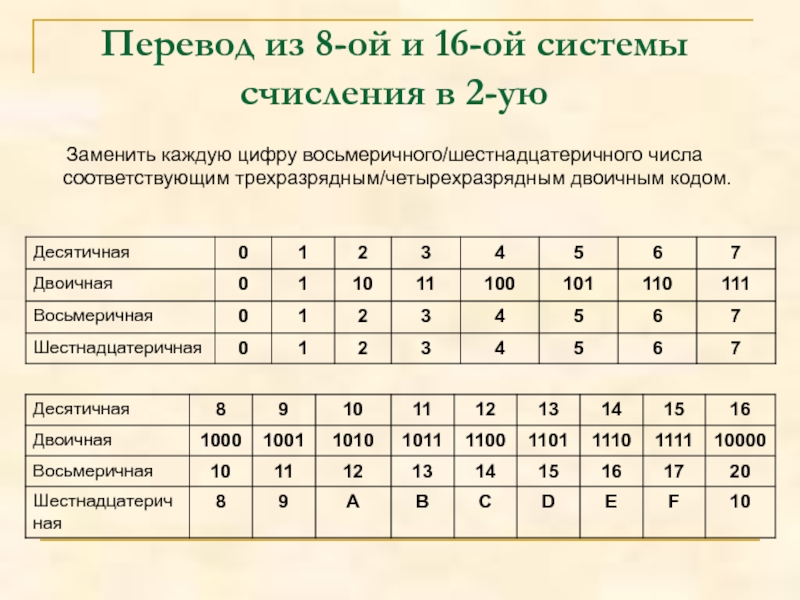
Слайд 8Перевод из 8-ой и 16-ой системы счисления в 2-ую
Заменить каждую цифру восьмеричного/шестнадцатеричного числа соответствующим трехразрядным/четырехразрядным двоичным кодом.
Слайд 9Перевод из 2-ой системы
счисления в 8-ую и 16-ую
Для перехода от двоичной к восьмеричной/шестнадцатеричной системе счисления поступают следующим образом: двигаясь от запятой влево и вправо, разбивают двоичное число на группы по 3/4 разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем каждую группу из 3/4 разрядов заменяют соответствующей восьмеричной/шестнадцатеричной цифрой.