- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Оптимизация нелинейных систем презентация
Содержание
- 1. Оптимизация нелинейных систем
- 3. Если в математической модели оптимизационной задачи имеются
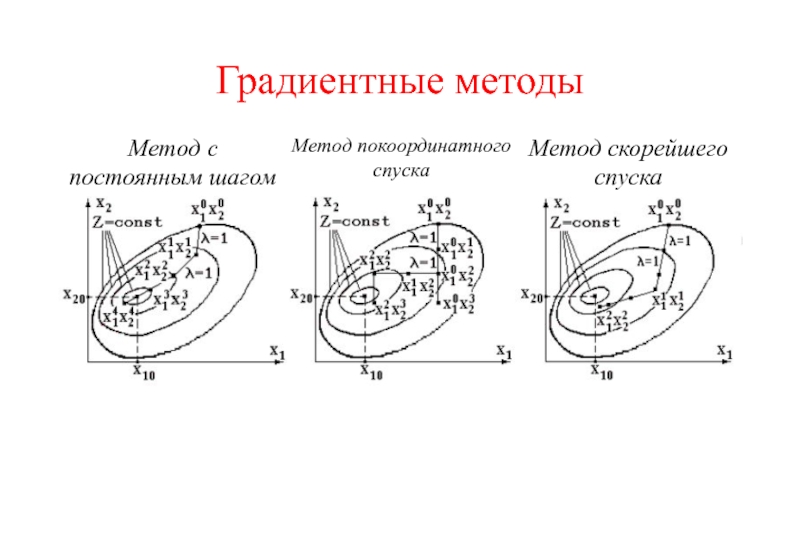
- 4. Метод с постоянным шагом Метод покоординатного спуска Метод скорейшего спуска Градиентные методы
- 5. Метод с постоянным шагом Метод покоординатного спуска
- 6. В результате вычислительного процесса последовательно осуществляется «спуск»
- 7. Метод множителей Лагранжа
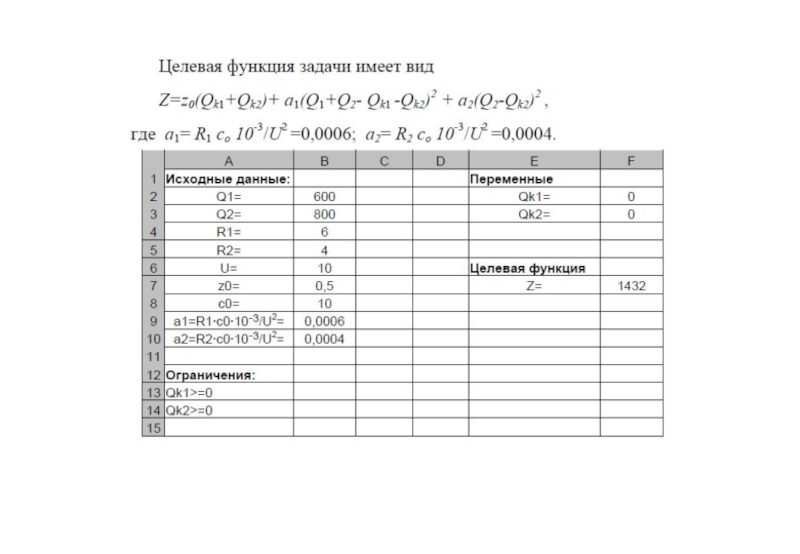
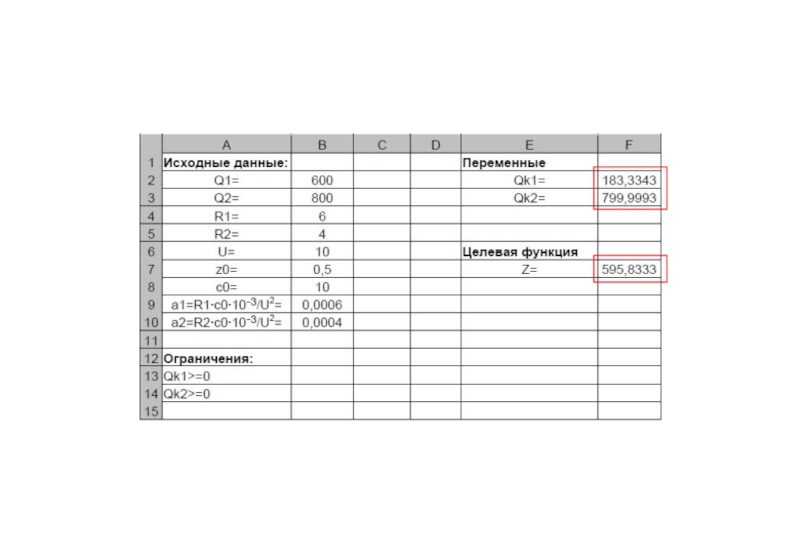
- 12. Решение задач нелинейного программирования в EXCEL
- 16. Спасибо за внимание!
Если в математической модели оптимизационной задачи имеются нелинейные зависимости, для решения этой задачи используются методы нелинейного программирования.
Слайд 3 Если в математической модели оптимизационной задачи имеются нелинейные зависимости, для решения
этой задачи используются методы нелинейного программирования.
Слайд 4
Метод с постоянным шагом
Метод покоординатного спуска
Метод скорейшего спуска
Градиентные методы
Слайд 5Метод с постоянным шагом
Метод покоординатного спуска
Метод скорейшего спуска
Градиентные методы
Исходное (нулевое) приближение
x10, x20.
2. Z0 = Z(x10, x20).
3. grad Z(x10, x20)
4. Шаг длиной λ в направлении −grad Z(x10, x20) → точка (x11,x21)
…
4. Определение большей по модулю частной производной ∂Z/∂xi → изменение xi на λ до тех пор, пока Z не начнет увеличиваться → изменение другой координаты → точка (x11,x21)
…
4. Определение оптимальной длины шага λопт, например, параболической аппроксимацией → шаг длиной λопт в направлении −grad Z(x10, x20) → точка (x11,x21)
…
Слайд 6 В результате вычислительного процесса последовательно осуществляется «спуск» к минимуму функции Z.
Вычислительная процедура заканчивается, когда относительное изменение целевой функции на предыдущем i-м и последующем (i+1)-м шагах оказывается меньше заданной точности вычислений ε:
