Лекция 3
Тема2. Оптимизационные модели.
Элементы линейного программирования (продолжение)
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Оптимизационные модели. Элементы линейного программирования. (Лекция 3. Тема 2) презентация
Содержание
- 1. Оптимизационные модели. Элементы линейного программирования. (Лекция 3. Тема 2)
- 2. 2.4. Двойственная задача и ее решение. Целочисленное программирование
- 3. Каждой задаче ЛП можно определенным образом поставить
- 4. 1) в одной задаче ищут максимум целевой
- 5. Такие задачи решаются методами целочисленного программирования.
- 6. 2.5. Симплекс-метод решения задач ЛП
- 7. Графический способ решения задачи ЛП показывает, что
- 8. ? Симплекс – это выпуклый многоугольник в
- 9. Переход от геометрического способа решения задачи ЛП
- 11. Требования к ограничениям: 1. Все ограничения (включая
- 12. Преобразование неравенств в равенства Неравенства любого типа
- 13. Пример 2.4. Преобразовать следующую задачу ЛП в стандартную форму: при выполнении следующих условий:
- 14. Действия:
- 15. Получаем: при выполнении следующих условий:
- 16. 2.5.2. Основы симплекс-метода
- 17. Рассмотрим общую ЗЛП с m ограничениями и
- 18. Как правило, число уравнений задачи меньше числа переменных (т. е. m
- 19. Получение одного из базисных решений основано на
- 20. При использовании первых m переменных такая система имеет следующий вид: (2.2)
- 21. При записи системы в каноническом виде все
- 22. ? Базисное решение называется допустимым базисным решением,
- 23. Поэтому ЗЛП можно решать посредством перебора конечного
- 24. СМ разработал американский ученый Дж. Данциг в 1947 г.
- 25. Гарантии результативности СМ обеспечиваются следующей теоремой.
- 26. 2.5.3. Вычислительный алгоритм симплекс-метода
- 27. Рассмотрим работу алгоритма на примере компании Mikks. Математическая модель:
- 28. Математическая модель: В стандартной форме:
- 29. В стандартной форме: Замечание. Если целевую
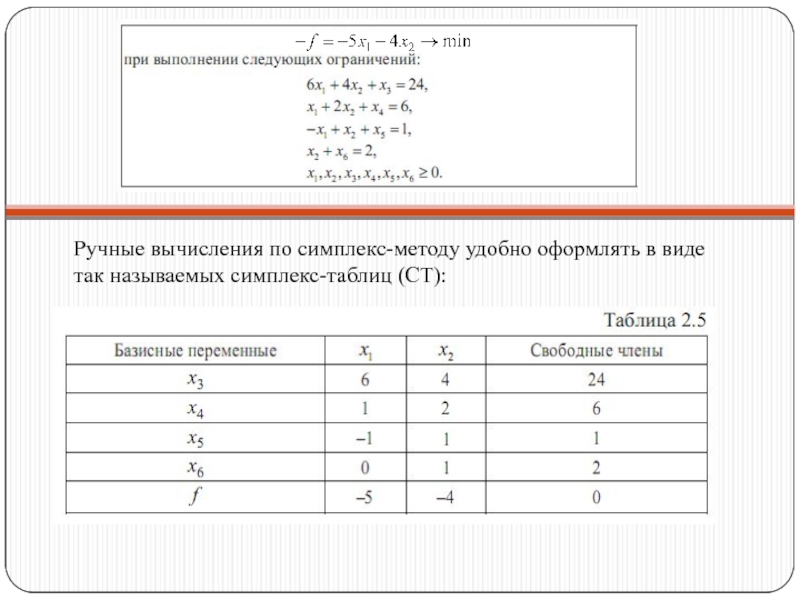
- 30. Ручные вычисления по симплекс-методу удобно оформлять в виде так называемых симплекс-таблиц (СТ):
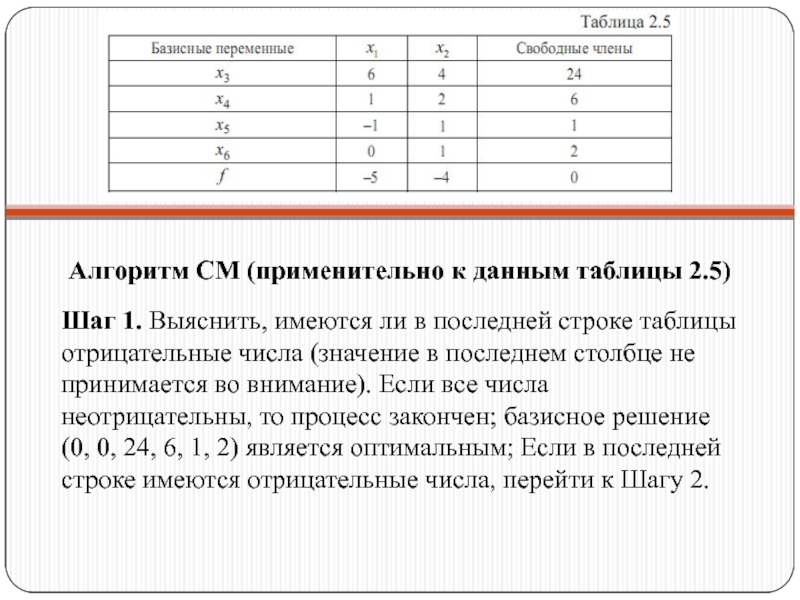
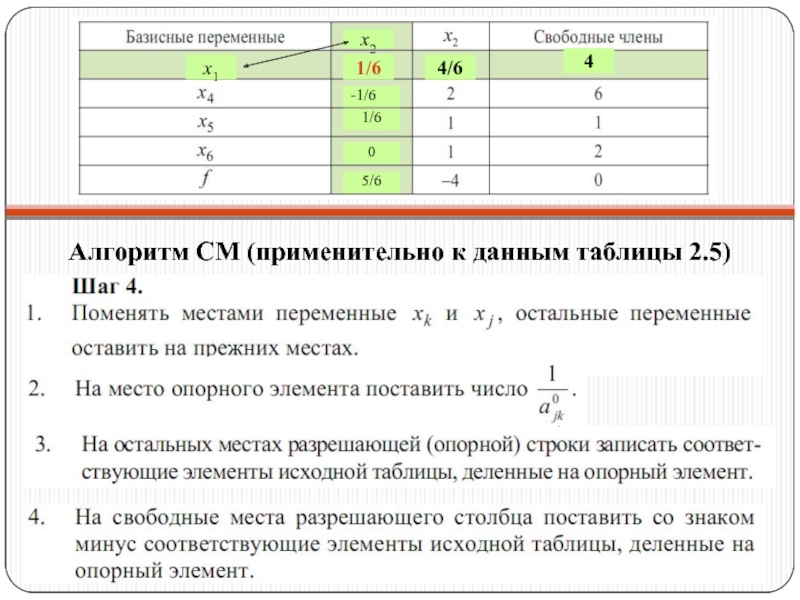
- 31. Алгоритм СМ (применительно к данным таблицы 2.5)
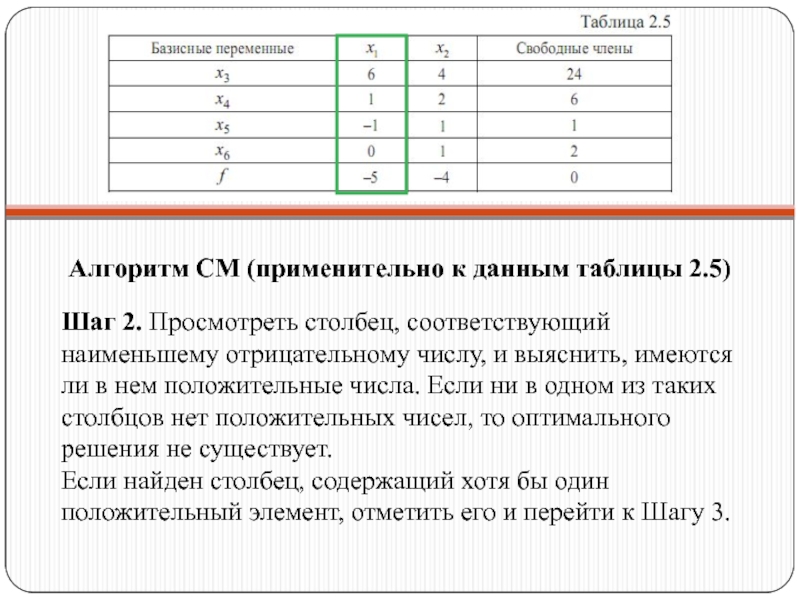
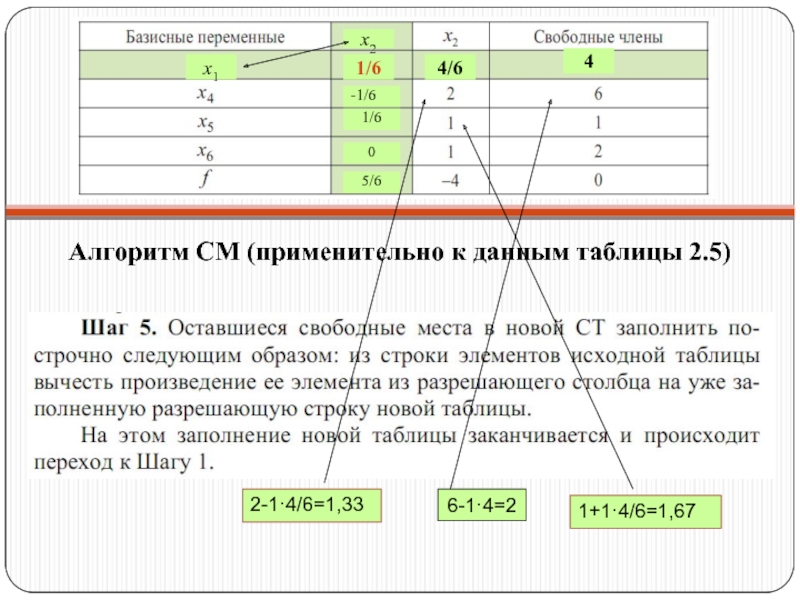
- 32. Алгоритм СМ (применительно к данным таблицы 2.5)
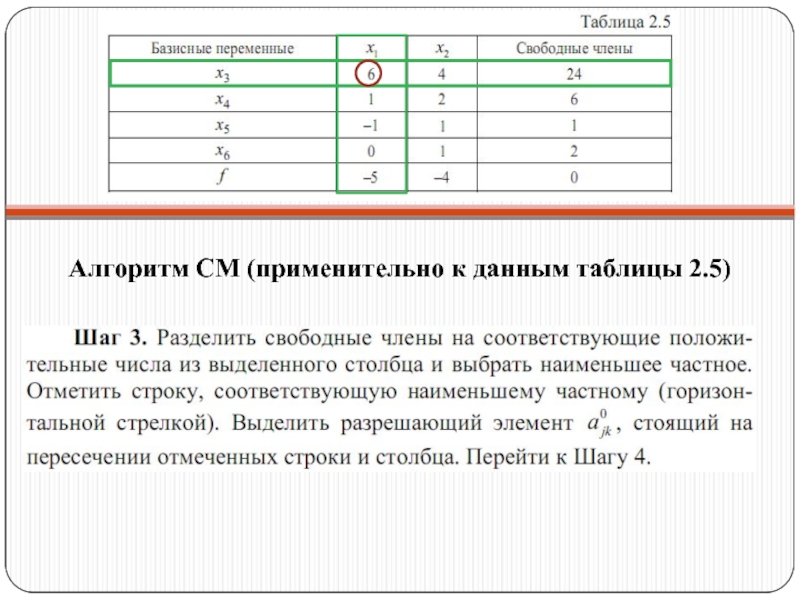
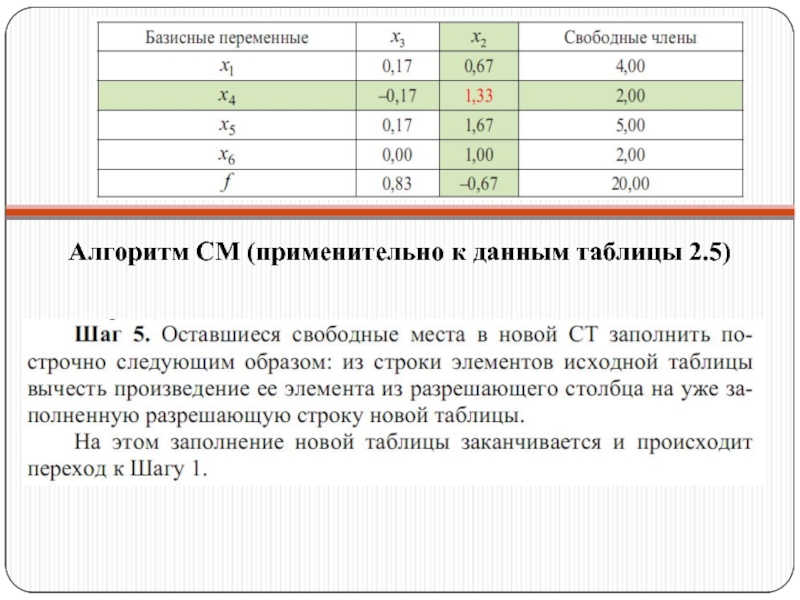
- 33. Алгоритм СМ (применительно к данным таблицы 2.5)
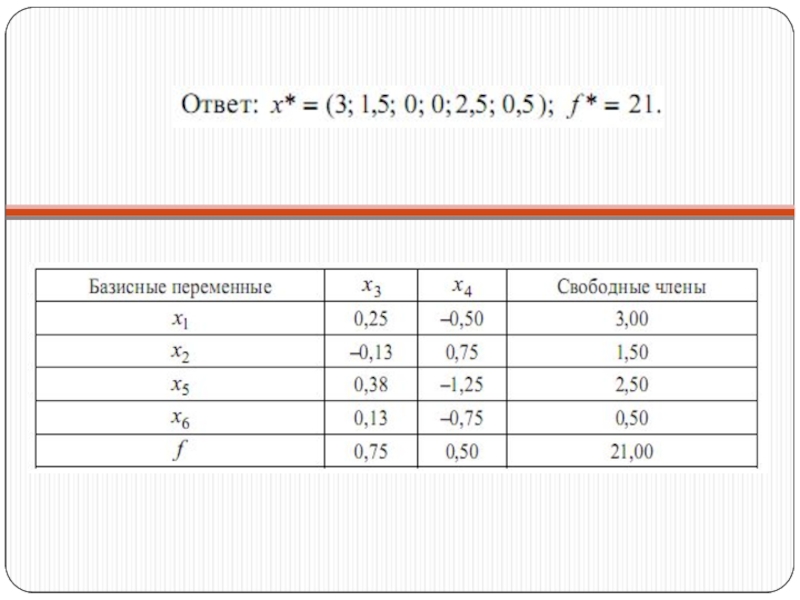
- 34. Алгоритм СМ (применительно к данным таблицы 2.5)
- 35. Алгоритм СМ (применительно к данным таблицы 2.5)
- 36. Алгоритм СМ (применительно к данным таблицы 2.5)
- 38. Спасибо за внимание!
- 39. Контрольные вопросы: Дайте определение двойственной задачи по
Слайд 12.4. Двойственная задача и ее решение. Целочисленное программирование
2.5. Симплекс-метод решения задач
Слайд 3Каждой задаче ЛП можно определенным образом поставить в соответствие некоторую другую
Двойственная задача по отношению к общей задаче ЛП, состоящей в нахождении максимального значения функции
при ограничениях «с недостатком»
Слайд 41) в одной задаче ищут максимум целевой функции, в другой минимум;
2) обе задачи являются стандартными задачами линейного программирования, причем в задаче о максимуме все неравенства вида «≤», а в задаче о минимуме вида «≥»;
3) матрица системы ограничений одной задачи является транспонированной к матрице системы ограничений другой;
4) коэффициенты при переменных целевой функции одной задачи являются свободными членами ограничений другой;
5) число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче;
6) условия неотрицательности имеются в обеих задачах.
Свойства двойственных задач ЛП:
Слайд 5Такие задачи решаются методами целочисленного программирования.
Общая постановка задачи линейного программирования
Значительная часть задач по смыслу может иметь решения только в целых числах; например, число турбин, судов, животных может быть только целым числом.
Слайд 7Графический способ решения задачи ЛП показывает, что оптимальное решение этой задачи
Это является ключевой идеей при разработке общего алгебраического симплекс-метода для решения любой задачи ЛП.
Симплексный метод – это вычислительная процедура, основанная на принципе последовательного улучшения решений при переходе от одной базисной точки (базисного решения) к другой. При этом значение целевой функции улучшается.
Базисным решением является одно из допустимых решений, находящихся в вершинах области допустимых значений. Проверяя на оптимальность вершину за вершиной симплекса, приходят к искомому оптимуму. На этом принципе основан симплекс-метод.
Слайд 8? Симплекс – это выпуклый многоугольник в n-мерном пространстве с n+1
Симплексный метод – это вычислительная процедура, основанная на принципе последовательного улучшения решений при переходе от одной базисной точки (базисного решения) к другой. При этом значение целевой функции улучшается.
Базисным решением является одно из допустимых решений, находящихся в вершинах области допустимых значений. Проверяя на оптимальность вершину за вершиной симплекса, приходят к искомому оптимуму. На этом принципе основан симплекс-метод.
Слайд 9Переход от геометрического способа решения задачи ЛП к симплекс-методу лежит через
2.5.1. Стандартная форма задач линейного программирования
Слайд 11Требования к ограничениям:
1. Все ограничения (включая ограничения неотрицательности переменных) преобразуются в
2. Все переменные неотрицательные.
3. Целевую функцию следует или максимизировать, или минимизировать.
Слайд 12Преобразование неравенств в равенства
Неравенства любого типа (со знаками неравенств «≤» или
Для неравенств типа «≤» в левую часть неравенства вводится неотрицательная переменная
Модель компании Mikks
Для неравенств типа «≥» в левую часть неравенства вводится неположительная переменная
Модели «диеты»
Слайд 13Пример 2.4. Преобразовать следующую задачу ЛП в стандартную форму:
при выполнении
Слайд 17Рассмотрим общую ЗЛП с m ограничениями и n переменными, записанную в
(2.1)
Слайд 18Как правило, число уравнений задачи меньше числа переменных (т. е. m
Задача состоит в том, чтобы найти наилучшее решение в смысле принятого критерия (минимума целевой функции).
Оптимальное решение представляет собой одну из вершин многогранника допустимой области. Другими словами, оптимальное решение - это одно из базисных решений.
Слайд 19Получение одного из базисных решений основано на методе решения систем линейных
Основная идея: сведение системы m уравнений с n неизвестными к ступенчатому виду при помощи элементарных операций над строками:
1) умножение любого уравнения системы на положительное или отрицательное число;
2) прибавление к любому уравнению другого уравнения системы, умноженного на положительное или отрицательное число.
Слайд 21При записи системы в каноническом виде все ее решения можно получить,
? Базисным решением системы (2.2) называется решение, полученное при нулевых значениях небазисных переменных.
Например, в системе (2.2) одно из базисных решений задается как
(2.3)
Слайд 22? Базисное решение называется допустимым базисным решением, если значения входящих в
что эквивалентно условию:
Так как различные базисные решения системы (2.2) соответствуют различным вариантам выбора (m) из общего числа (n) переменных хj, то число допустимых базисных решений (угловых точек) не превышает
Слайд 23Поэтому ЗЛП можно решать посредством перебора конечного числа угловых точек допустимого
Наихудший вариант решения ЗЛП, так как требует огромного объема вычислений.
Пример: если n=50, m=25 (задача небольшой размерности), то количество переборов составит
Обычно
Слайд 24СМ разработал американский ученый Дж. Данциг в 1947 г.
Идея симплекс-метода (СМ) состоит
Этот метод называют также методом последовательного улучшения решения (плана).
Джордж Бернард Данциг
(1914-2005)
Слайд 25Гарантии результативности СМ обеспечиваются следующей теоремой.
Теорема (о конечности алгоритма симплекс-метода).
Слайд 29В стандартной форме:
Замечание. Если целевую функцию необходимо максимизировать, то предварительно
Слайд 30Ручные вычисления по симплекс-методу удобно оформлять в виде так называемых симплекс-таблиц
Слайд 31Алгоритм СМ (применительно к данным таблицы 2.5)
Шаг 1. Выяснить, имеются ли
Слайд 32Алгоритм СМ (применительно к данным таблицы 2.5)
Шаг 2. Просмотреть столбец, соответствующий
Если найден столбец, содержащий хотя бы один положительный элемент, отметить его и перейти к Шагу 3.
Слайд 35Алгоритм СМ (применительно к данным таблицы 2.5)
x1
x2
1/6
4/6
4
-1/6
1/6
0
5/6
2-1·4/6=1,33
6-1·4=2
1+1·4/6=1,67
Слайд 39Контрольные вопросы:
Дайте определение двойственной задачи по отношению к общей задаче линейного
Сформулируйте свойства двойственных задач линейного программирования.
Какие задачи решаются методами целочисленного программирования?
Как в канонической (стандартной) форме задается задача линейного программирования?
Какие требования предъявляются к стандартной форме записи задачи линейного программирования?
Перечислите действия необходимые для преобразования задачи линейного программирования в стандартную форму.
В чем состоит основная идея симплекс-метода? Какое решение называется базисным? Как следует поступить, если целевую функцию необходимо максимизировать?
Сформулируйте теорему о конечности симплекс-метода.
Опишите алгоритм симплекс-метода.