- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обобщенные задачи коммивояжера и планарные графы презентация
Содержание
- 1. Обобщенные задачи коммивояжера и планарные графы
- 2. СОДЕРЖАНИЕ Обобщенные задачи коммивояжера и их решение
- 3. ЧАСТЬ 1 ОБОБЩЕННЫЕ ЗАДАЧИ КОММИВОЯЖЕРА
- 4. Содержательные постановки обобщенных задач коммивояжера 1. Разомкнутая
- 5. Основные отличия от «классических» постановок 1. К
- 6. Графовая интерпретация «классической» замкнутой задачи коммивояжера
- 7. Подмножество «обязательных» вершин : {1, 2, 4}.
- 8. Обозначения и определения
- 9. Формальная постановка «классической» аддитивной замкнутой задачи коммивояжера
- 10. Формальная постановка обобщенной аддитивной замкнутой задачи коммивояжера
- 11. Решение обобщенной замкнутой задачи коммивояжера перебором (обязательными
- 12. САМОСТОЯТЕЛЬНО На орграфе G(X,U), заданном матрицей М,
- 13. Графовая интерпретация «классической» разомкнутой задачи коммивояжера
- 14. Формальная постановка «классической» аддитивной разомкнутой задачи коммивояжера
- 15. Подмножество «обязательных» вершин : {1, 2, 4},
- 16. Формальная постановка «обобщенной» аддитивной разомкнутой задачи коммивояжера
- 17. Решение обобщенной разомкнутой задачи коммивояжера перебором (обязательными
- 18. Самостоятельно Решить перебором разомкнутую обобщенную задачу коммивояжера
- 19. ЧАСТЬ 2 Связь задачи на разрыв контуров в сильносвязном орграфе и обобщенной задачи коммивояжера
- 20. Алгоритм 1 Шаг 1. На сильносвязном планарном
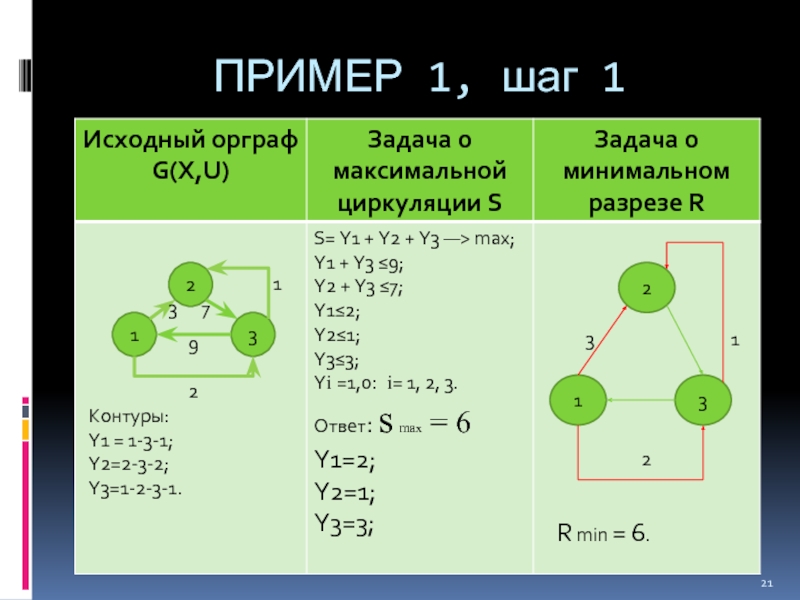
- 21. ПРИМЕР 1, шаг 1 1 2 3
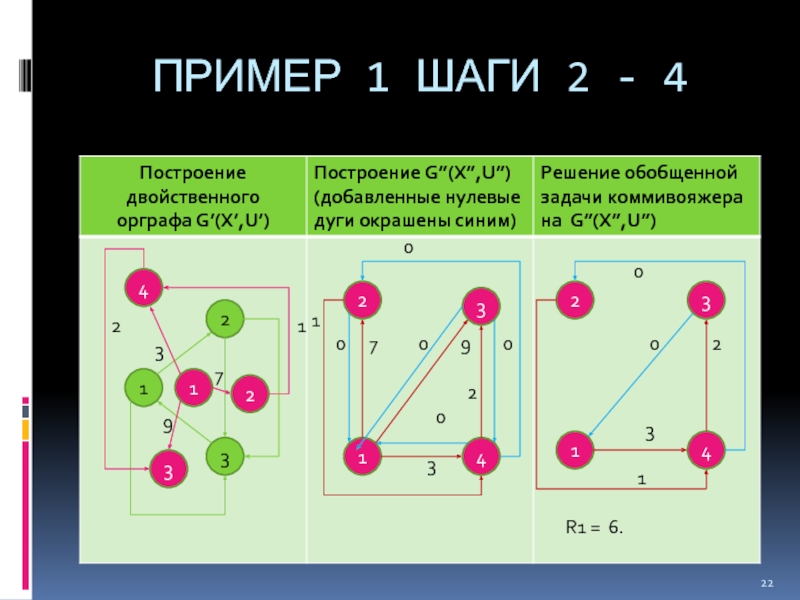
- 22. ПРИМЕР 1 ШАГИ 2 - 4 1
- 23. САМОСТОЯТЕЛЬНО Пользуясь приведенной ниже матрицей М построить
Слайд 2СОДЕРЖАНИЕ
Обобщенные задачи коммивояжера и их решение перебором.
Связь обобщенной задачи коммивояжера и
Слайд 4Содержательные постановки обобщенных задач коммивояжера
1. Разомкнутая постановка задачи: коммивояжер должен объехать
2. Замкнутая постановка задачи: коммивояжер должен объехать заданное подмножество городов вернуться в город из которого стартовал, затратив минимум средств на путешествие либо минимум средств на максимальный переход.
Слайд 5Основные отличия от «классических» постановок
1. К посещению коммивояжером обязательны только вершины
2. Отсутствует ограничение на число посещений каждой вершины.
Слайд 6Графовая интерпретация «классической» замкнутой задачи коммивояжера
1
2
7
4
3
5
6
Гамильтонов
Гамильтонов контур а2=5,3,4,6,1,2,7,5 -.
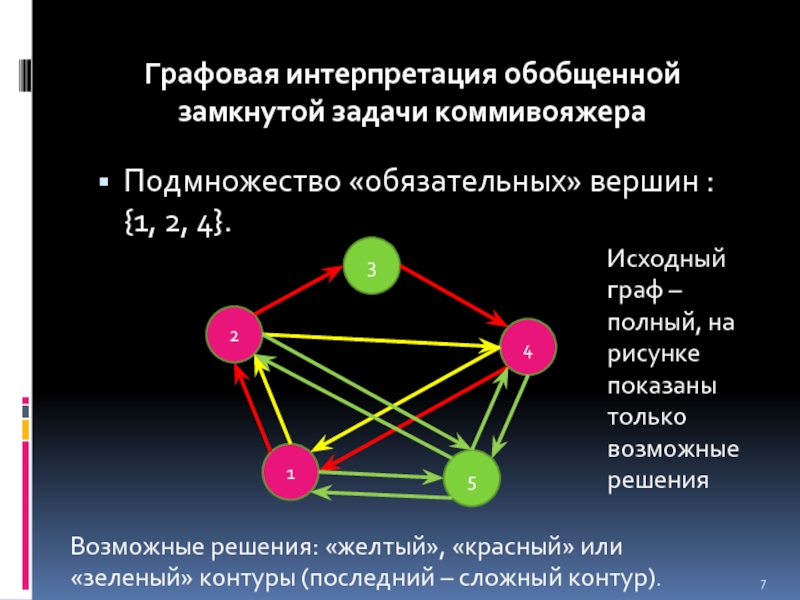
Слайд 7Подмножество «обязательных» вершин : {1, 2, 4}.
Графовая интерпретация обобщенной замкнутой задачи
2
5
1
4
3
Возможные решения: «желтый», «красный» или «зеленый» контуры (последний – сложный контур).
Исходный граф – полный, на рисунке показаны только возможные решения
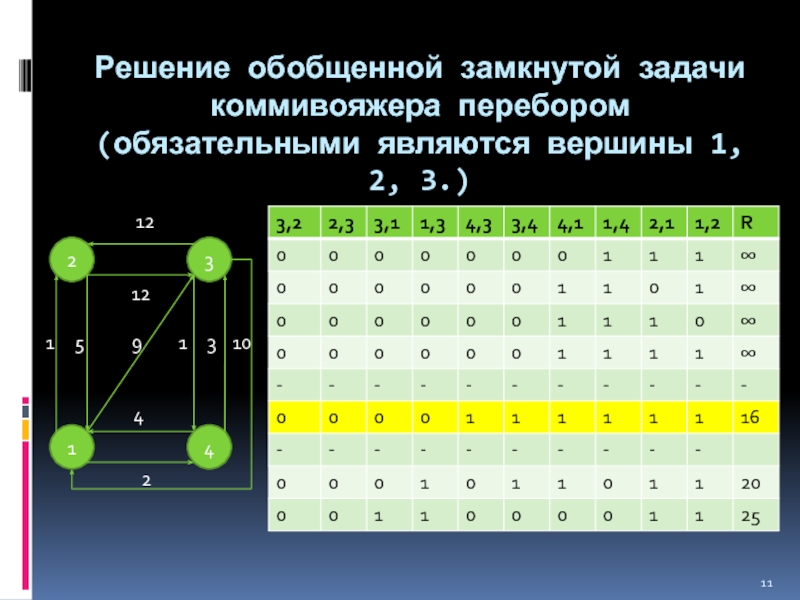
Слайд 11Решение обобщенной замкнутой задачи коммивояжера перебором (обязательными являются вершины 1, 2,
2
3
4
1
12
12
1 5 9 1 3 10
4
2
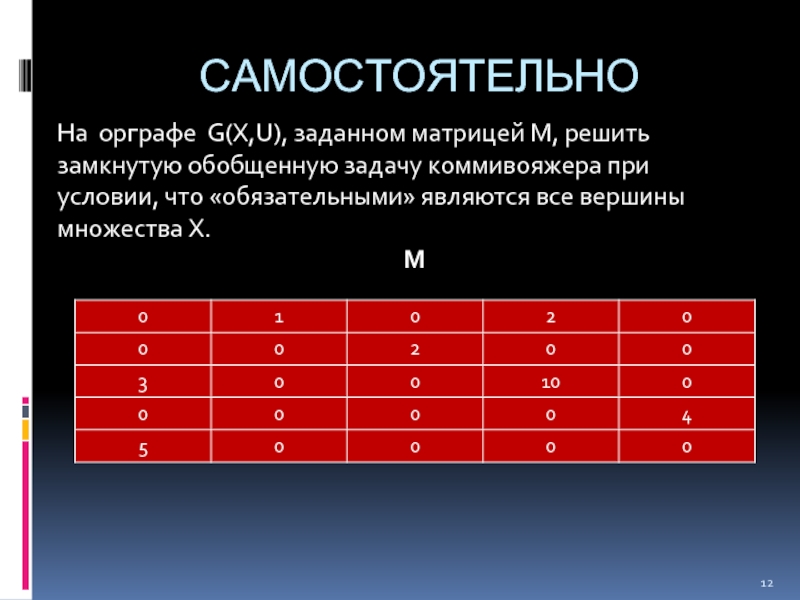
Слайд 12САМОСТОЯТЕЛЬНО
На орграфе G(X,U), заданном матрицей М, решить замкнутую обобщенную задачу коммивояжера
М
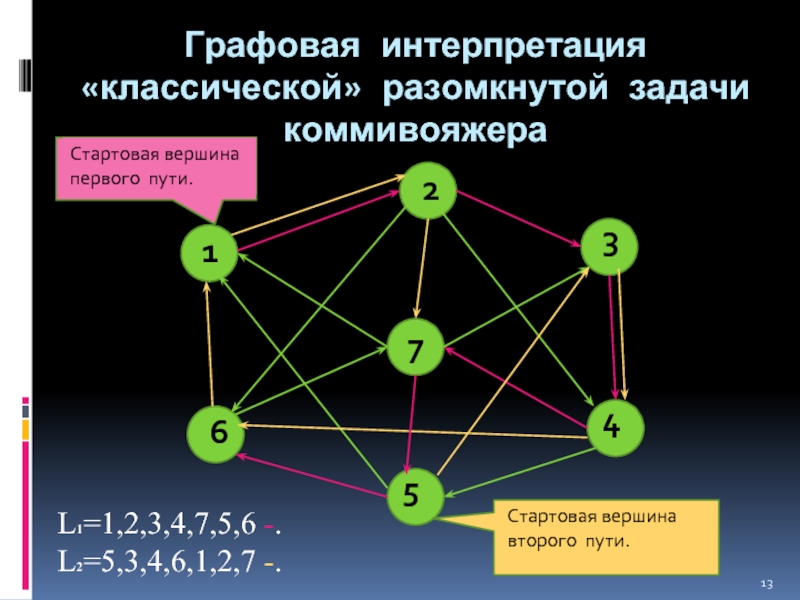
Слайд 13Графовая интерпретация «классической» разомкнутой задачи коммивояжера
1
2
7
4
3
5
6
L1=1,2,3,4,7,5,6
L2=5,3,4,6,1,2,7 -.
Стартовая вершина первого пути.
Стартовая вершина второго пути.
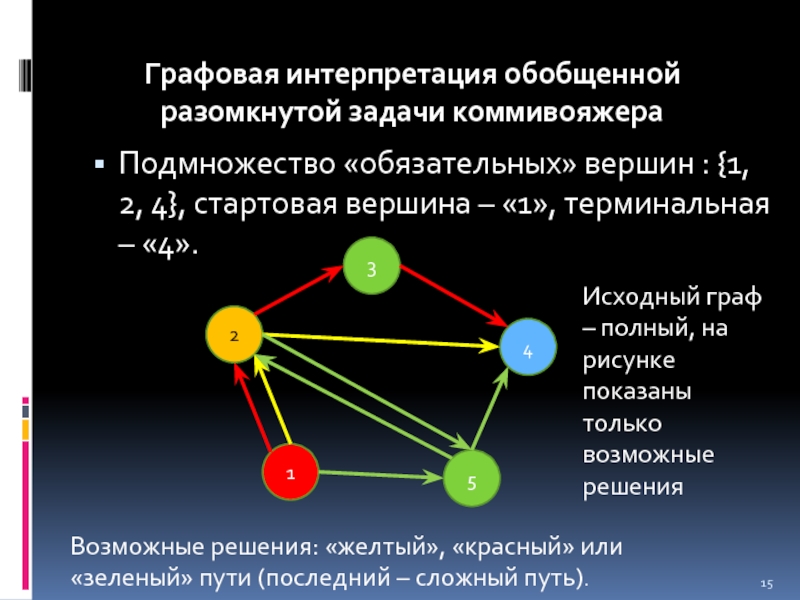
Слайд 15Подмножество «обязательных» вершин : {1, 2, 4}, стартовая вершина – «1»,
Графовая интерпретация обобщенной разомкнутой задачи коммивояжера
2
5
1
4
3
Возможные решения: «желтый», «красный» или «зеленый» пути (последний – сложный путь).
Исходный граф – полный, на рисунке показаны только возможные решения
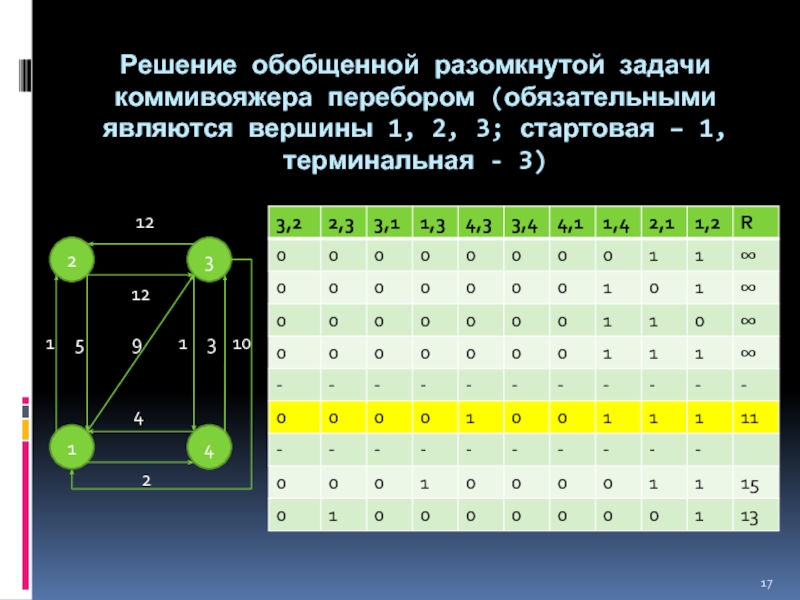
Слайд 17Решение обобщенной разомкнутой задачи коммивояжера перебором (обязательными являются вершины 1, 2,
2
3
4
1
12
12
1 5 9 1 3 10
4
2
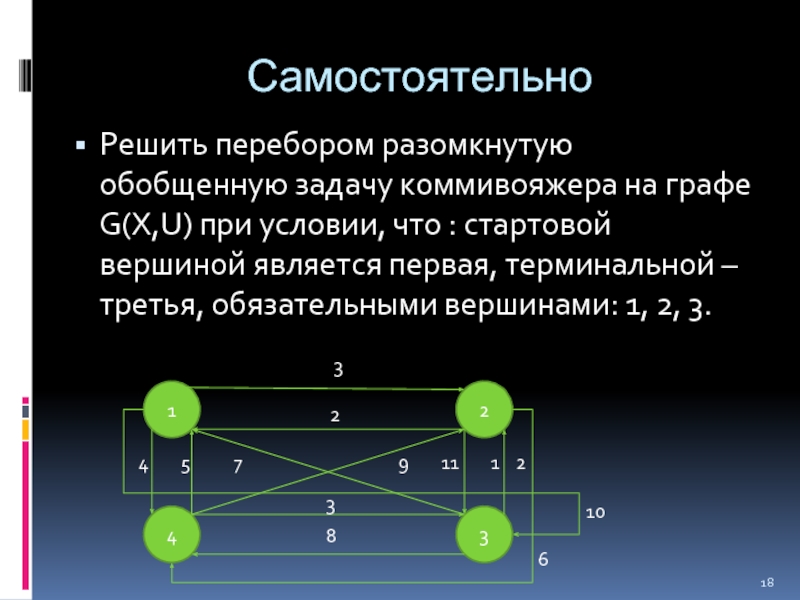
Слайд 18Самостоятельно
Решить перебором разомкнутую обобщенную задачу коммивояжера на графе G(X,U) при условии,
1
4
3
2
3
2
4 5 7 9 11 1 2
10
8
6
3
Слайд 19ЧАСТЬ 2
Связь задачи на разрыв контуров в сильносвязном орграфе и обобщенной
Слайд 20Алгоритм 1
Шаг 1. На сильносвязном планарном взвешенном орграфе G(X,U) определить величину
Шаг 2. Построить орграф G’(X’,U’), двойственный графу G(X,U).
Шаг 3. Модифицировать G’(X’,U’), добавив к каждой дуге множества U’ параллельную и встречно ориентированную дугу с нулевым весом. Полученный орграф обозначить G”(X”,U”).
Шаг 4. На G”(X”,U”) решить обобщенную замкнутую задачу коммивояжера при условии, что множество обязательных вершин равно Х”. Длину пути коммивояжера обозначить R1.
Шаг 5. Сравнить величины R, S, и R1.
Слайд 23САМОСТОЯТЕЛЬНО
Пользуясь приведенной ниже матрицей М построить граф G(X,U), определить на нем
M