- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Некоторые понятия алгебры логики, логические элементы компьютера презентация
Содержание
- 1. Некоторые понятия алгебры логики, логические элементы компьютера
- 2. Оценка сообщений с позиций алгебры логики
- 3. Логические операции В информатике вместо термина «логическая
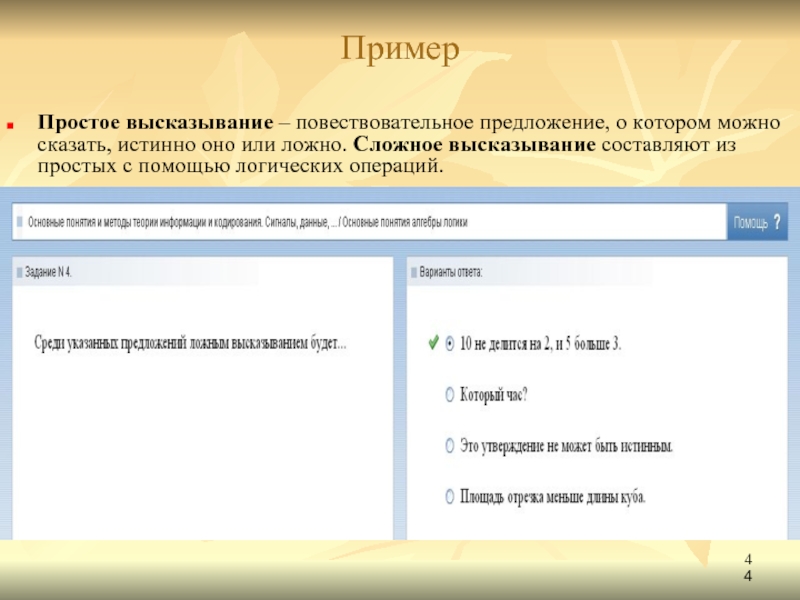
- 4. Пример Простое высказывание – повествовательное предложение, о
- 5. 4) Операция XOR – исключающее ИЛИ. Обозначается
- 6. Основными операциями считаются конъюнкция, дизъюнкция и отрицание.
- 7. Основные законы равносильности алгебры логики Эквивалентные
- 8. Логические элементы компьютера Устройство, которое выполняет
- 9. 3) Элемент «НЕ» (NOT) – инвертор. Сигнал
- 10. Триггеры Вентили используют для конструирования триггеров (trigger
- 11. Величина, сохраняемая в триггере, определяется его выходным
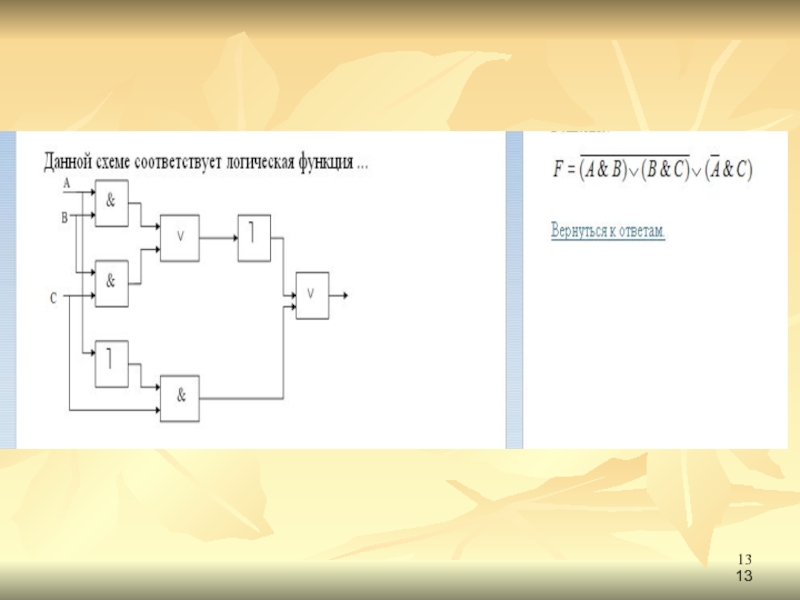
- 12. Логические схемы
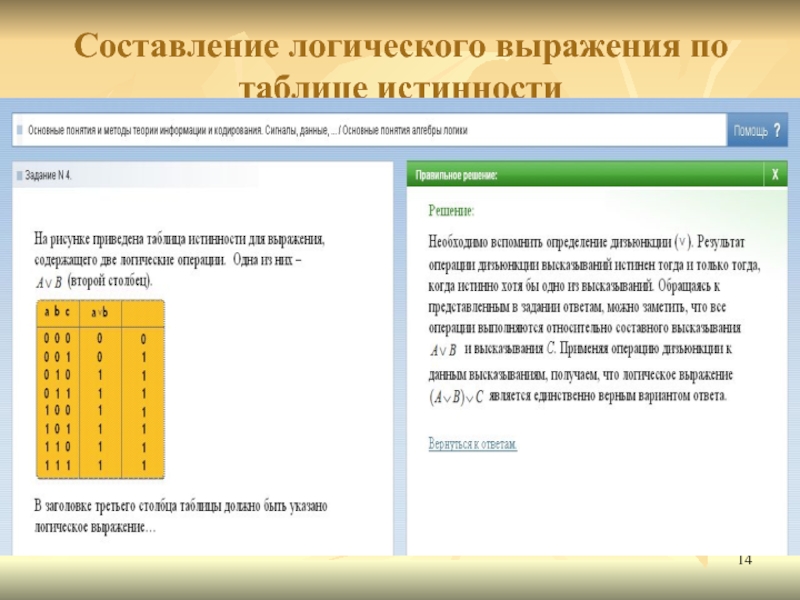
- 14. Составление логического выражения по таблице истинности
- 15. Дополнение
- 16. Законов и правил логики очень много. Cамые
- 17. 6) Законы идемпотентности: А ∨ А
- 18. Примеры преобразования логических выражений
Слайд 2Оценка сообщений с позиций алгебры логики
Алгебра логики — это математический
аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания. Создателем алгебры логики (ХIХ век) считается английский математик Джордж Буль, в честь которого эта алгебра названа булевой.
Логическим высказыванием называют любое повествовательное предложение, в отношении которого однозначно известно, истинно оно или ложно. Так, например, о сообщении «Белый гриб съедобен» можно сказать, что оно истинное высказывание. Сообщение «Все грибы съедобны» – пример ложного высказывания. Таким образом, алгебра логики по существу двузначна.
Высказывания, образованные из других высказываний с помощью логических связок («и», «или», и др.), называются сложными или составными. Высказывания, не являющиеся составными, называются элементарными. Например, высказывания «Три – число нечетное» и «Три – число простое» являются элементарными, тогда как высказывание «Три – число нечетное и простое» – составное. В последнем высказывании союз «и» употребляется как логическая связка
Cложное высказывание, истинное для всех значений входящих в него переменных, называется тождественно истинным или тавтологией. Тавтологиями являются все математические законы, например: истинно для любых a и b следующее выражение: а2 – в2 = (а-в)(а+в).
Сложное высказывание, ложное при всех значениях входящих в него переменных, называется тождественно ложным.
Если значения сложных высказываний совпадают при всех возможных значениях входящих в них переменных, то такие высказывания называют равносильными, тождественными или эквивалентными.
Логическим высказыванием называют любое повествовательное предложение, в отношении которого однозначно известно, истинно оно или ложно. Так, например, о сообщении «Белый гриб съедобен» можно сказать, что оно истинное высказывание. Сообщение «Все грибы съедобны» – пример ложного высказывания. Таким образом, алгебра логики по существу двузначна.
Высказывания, образованные из других высказываний с помощью логических связок («и», «или», и др.), называются сложными или составными. Высказывания, не являющиеся составными, называются элементарными. Например, высказывания «Три – число нечетное» и «Три – число простое» являются элементарными, тогда как высказывание «Три – число нечетное и простое» – составное. В последнем высказывании союз «и» употребляется как логическая связка
Cложное высказывание, истинное для всех значений входящих в него переменных, называется тождественно истинным или тавтологией. Тавтологиями являются все математические законы, например: истинно для любых a и b следующее выражение: а2 – в2 = (а-в)(а+в).
Сложное высказывание, ложное при всех значениях входящих в него переменных, называется тождественно ложным.
Если значения сложных высказываний совпадают при всех возможных значениях входящих в них переменных, то такие высказывания называют равносильными, тождественными или эквивалентными.
Слайд 3Логические операции
В информатике вместо термина «логическая связка» принято употреблять термин «логическая
операция».
Рассмотрим действие основных логических операций, принимая, что 0 – представляет значение «ложь», а 1 – логическое значение «истина».
1) Операция AND (И)- конъюнкция (лат. conjunctio – соединение), логическое умножение. Обозначается символом ∧, иногда &.
Она реализует следующую конструкцию логического высказывания: «результат операции будет истинным только в том случае, если оба входных сообщения истинны»:
1∧1=1,
1∧0=0,
0∧1=0,
0∧0=0.
2) Операция OR (ИЛИ) – дизъюнкция (лат. disjunctio – разделение). Обозначается символом ∨.
Реализует словесную конструкцию: «результат будет истинным, если истинно хотя бы одно из входных сообщений»:
1∨1=1,
1∨0=1,
0∨1=1,
0∨0=0.
3) Операция NOT (НЕ) – логическое отрицание. Обозначается символом ¬, иногда ¯.
Отличается от рассмотренных операций тем, что имеет только одно входное значение, причем результатом всегда будет значение противоположное, например:
¬1=0, ¬0=1.
Рассмотрим действие основных логических операций, принимая, что 0 – представляет значение «ложь», а 1 – логическое значение «истина».
1) Операция AND (И)- конъюнкция (лат. conjunctio – соединение), логическое умножение. Обозначается символом ∧, иногда &.
Она реализует следующую конструкцию логического высказывания: «результат операции будет истинным только в том случае, если оба входных сообщения истинны»:
1∧1=1,
1∧0=0,
0∧1=0,
0∧0=0.
2) Операция OR (ИЛИ) – дизъюнкция (лат. disjunctio – разделение). Обозначается символом ∨.
Реализует словесную конструкцию: «результат будет истинным, если истинно хотя бы одно из входных сообщений»:
1∨1=1,
1∨0=1,
0∨1=1,
0∨0=0.
3) Операция NOT (НЕ) – логическое отрицание. Обозначается символом ¬, иногда ¯.
Отличается от рассмотренных операций тем, что имеет только одно входное значение, причем результатом всегда будет значение противоположное, например:
¬1=0, ¬0=1.
Слайд 4Пример
Простое высказывание – повествовательное предложение, о котором можно сказать, истинно оно
или ложно. Сложное высказывание составляют из простых с помощью логических операций.
Слайд 54) Операция XOR – исключающее ИЛИ. Обозначается символом ⊗.
Реализует конструкцию «результат
будет истинным, если истинно либо то, либо другое из входных значений, но не оба одновременно», например:
1⊗1=0,
1⊗0=1,
0⊗1=1,
0⊗0=0.
5) Импликация (лат. implico – тесно связаны). Обозначается символом →.
Выражается в конструкциях: “если ..., то”, “из ... следует”, “... влечет ...”. Например, «из A следует B», «если верно сообщение А, то верно и В», «наступление события А влечет наступление события В»: A→B.
Импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное (истинная предпосылка ведет к ложному выводу):
1→1=1,
1→0=0,
0→1=1,
0→0=1.
6) Эквиваленция (или двойная импликация). Обозначается символом ↔ или ∼.
Выражается высказываниями типа “тогда и только тогда”, "необходимо и достаточно”, “равносильно”. Например, «A равносильно B» (и наоборот)», «для наступления события А необходимо и достаточно наступления события В»: A↔B.
Эквивалентность двух высказываний истинна, тогда и только тогда, когда оба эти высказывания истинны, или оба ложны:
1↔1=1,
1↔0=0,
0↔1=0,
0↔0=1.
1⊗1=0,
1⊗0=1,
0⊗1=1,
0⊗0=0.
5) Импликация (лат. implico – тесно связаны). Обозначается символом →.
Выражается в конструкциях: “если ..., то”, “из ... следует”, “... влечет ...”. Например, «из A следует B», «если верно сообщение А, то верно и В», «наступление события А влечет наступление события В»: A→B.
Импликация двух высказываний ложна тогда и только тогда, когда из истинного высказывания следует ложное (истинная предпосылка ведет к ложному выводу):
1→1=1,
1→0=0,
0→1=1,
0→0=1.
6) Эквиваленция (или двойная импликация). Обозначается символом ↔ или ∼.
Выражается высказываниями типа “тогда и только тогда”, "необходимо и достаточно”, “равносильно”. Например, «A равносильно B» (и наоборот)», «для наступления события А необходимо и достаточно наступления события В»: A↔B.
Эквивалентность двух высказываний истинна, тогда и только тогда, когда оба эти высказывания истинны, или оба ложны:
1↔1=1,
1↔0=0,
0↔1=0,
0↔0=1.
Слайд 6Основными операциями считаются конъюнкция, дизъюнкция и отрицание. Через них можно выразить
остальные.
Например, операция импликации выражается через отрицание и дизъюнкцию:
A→B = ¬ А∨В.
Операция эквивалентности заменяется двумя равносильными выражениями:
A↔B = (A ∧ B) ∨ (¬A ∧ ¬B),
A ↔ B = (A ∨ ¬B) ∧ (¬A ∨ B).
Порядок выполнения логических операций задается круглыми скобками. Иначе порядок действий следующий: сначала выполняется операция отрицания (NOT), затем конъюнкция (AND), после конъюнкции – дизъюнкция (OR или XOR) и в последнюю очередь – импликация и эквиваленция.
Пример сложного логического высказывания: А∨(B→C) ∧ D ↔ ¬ (A)
Порядок выполнения:
¬ (А) – инверсия
В → С – импликация
(В → С) ∧ D – конъюнкция
А ∨ (B → C) ∧ D – дизъюнкция
А ∨ (B → C) ∧ D = не(A) – эквивалентность
Например, операция импликации выражается через отрицание и дизъюнкцию:
A→B = ¬ А∨В.
Операция эквивалентности заменяется двумя равносильными выражениями:
A↔B = (A ∧ B) ∨ (¬A ∧ ¬B),
A ↔ B = (A ∨ ¬B) ∧ (¬A ∨ B).
Порядок выполнения логических операций задается круглыми скобками. Иначе порядок действий следующий: сначала выполняется операция отрицания (NOT), затем конъюнкция (AND), после конъюнкции – дизъюнкция (OR или XOR) и в последнюю очередь – импликация и эквиваленция.
Пример сложного логического высказывания: А∨(B→C) ∧ D ↔ ¬ (A)
Порядок выполнения:
¬ (А) – инверсия
В → С – импликация
(В → С) ∧ D – конъюнкция
А ∨ (B → C) ∧ D – дизъюнкция
А ∨ (B → C) ∧ D = не(A) – эквивалентность
Слайд 7Основные законы равносильности алгебры логики
Эквивалентные преобразования опираются на основные законы
- выражения, которые всегда истинны, независимо от значений переменных. Логические законы выражают в виде формул.
1) Закон тождества:
А = А – всякий объект тождественен сам себе, то есть «А есть А», где А – любое высказывание.
2) Закон исключенного третьего:
А ∨ ¬А = 1 – в один и тот же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано. Истинно либо А, либо не А.
3) Закон непротиворечия:
¬(¬ А ∧ А) = 1 – не могут быть одновременно истинными суждение и его отрицание. То есть, если высказывание А - истинно, то его отрицание ¬А должно быть ложным (и наоборот). Тогда их произведение будет всегда ложным, т.е. А ∧¬А =0.
Последняя формула часто используется при упрощении сложных логических выражений.
4) Закон двойного отрицания:
¬ ¬А = А – если отрицать дважды некоторое высказывание, то в результате получается исходное высказывание.
5) Законы, характеризующие свойства констант:
¬0 = 1,
¬ 1 = 0,
А ∨ 0 = А,
А ∧ 0 = 0,
А ∨ 1 = 1,
А ∧ 1 = А.
1) Закон тождества:
А = А – всякий объект тождественен сам себе, то есть «А есть А», где А – любое высказывание.
2) Закон исключенного третьего:
А ∨ ¬А = 1 – в один и тот же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано. Истинно либо А, либо не А.
3) Закон непротиворечия:
¬(¬ А ∧ А) = 1 – не могут быть одновременно истинными суждение и его отрицание. То есть, если высказывание А - истинно, то его отрицание ¬А должно быть ложным (и наоборот). Тогда их произведение будет всегда ложным, т.е. А ∧¬А =0.
Последняя формула часто используется при упрощении сложных логических выражений.
4) Закон двойного отрицания:
¬ ¬А = А – если отрицать дважды некоторое высказывание, то в результате получается исходное высказывание.
5) Законы, характеризующие свойства констант:
¬0 = 1,
¬ 1 = 0,
А ∨ 0 = А,
А ∧ 0 = 0,
А ∨ 1 = 1,
А ∧ 1 = А.
Слайд 8Логические элементы компьютера
Устройство, которое выполняет булеву операцию в компьютере (или
в другом техническом устройстве), называется логическим элементом или вентилем. Физически вентиль – это небольшая электрическая цепь, в которой два значения 0 и 1 представляются разными уровнями электрического напряжения.
Рассмотрим основные типы логических элементов, их условные графические обозначения, а также связанные с ними таблицы истинности:
1) Элемент «И» (AND), конъюнктор
Единица на выходе элемента «И» возникает только тогда, когда на оба входа поданы единицы. Это объясняет название элемента: единицы должны быть и на одном, и на другом входе..
2) Элемент «ИЛИ» (OR) – дизъюнктор
На выходе этого элемента возникает единица, когда на один ИЛИ на другой ИЛИ на оба сразу входа подана единица.
Рассмотрим основные типы логических элементов, их условные графические обозначения, а также связанные с ними таблицы истинности:
1) Элемент «И» (AND), конъюнктор
Единица на выходе элемента «И» возникает только тогда, когда на оба входа поданы единицы. Это объясняет название элемента: единицы должны быть и на одном, и на другом входе..
2) Элемент «ИЛИ» (OR) – дизъюнктор
На выходе этого элемента возникает единица, когда на один ИЛИ на другой ИЛИ на оба сразу входа подана единица.
Слайд 93) Элемент «НЕ» (NOT) – инвертор. Сигнал на выходе этого элемента
противоположен входному сигналу. Инвертор
4) Элемент «И-НЕ» (NAND) Вентиль NAND
Элемент И-НЕ работает точно так же как «И», только выходной сигнал противоположен.
Это легко понять по эквивалентной схеме элемента NAND.
5) Элемент «ИЛИ-НЕ» (NOR).
Работает как элемент «ИЛИ», но с инвертором на выходе. Элемент NOR
6) Элемент «Исключающее ИЛИ» (XOR)
Вентиль XOR
На выходе этого элемента появится единица лишь в том случае, если на входы поступят разные по значению сигналы: на одном – 1, на другом – 0.
4) Элемент «И-НЕ» (NAND) Вентиль NAND
Элемент И-НЕ работает точно так же как «И», только выходной сигнал противоположен.
Это легко понять по эквивалентной схеме элемента NAND.
5) Элемент «ИЛИ-НЕ» (NOR).
Работает как элемент «ИЛИ», но с инвертором на выходе. Элемент NOR
6) Элемент «Исключающее ИЛИ» (XOR)
Вентиль XOR
На выходе этого элемента появится единица лишь в том случае, если на входы поступят разные по значению сигналы: на одном – 1, на другом – 0.
Слайд 10Триггеры
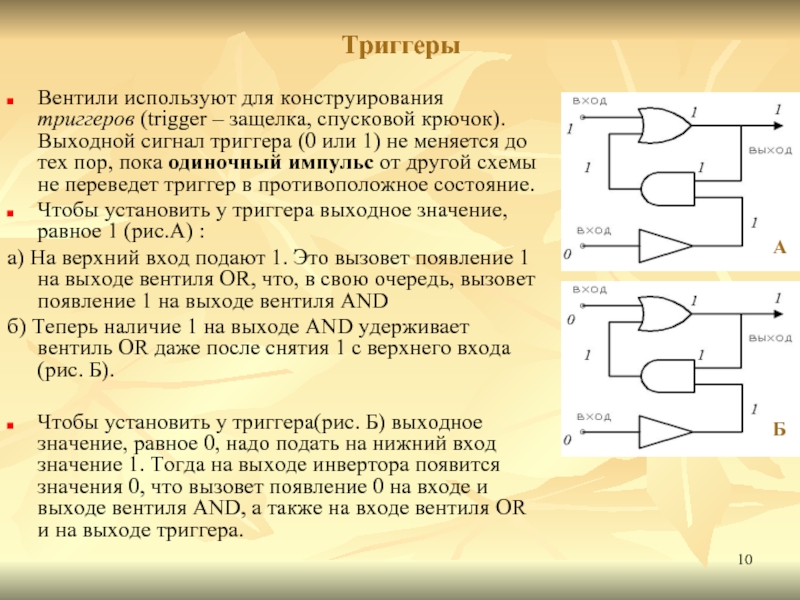
Вентили используют для конструирования триггеров (trigger – защелка, спусковой крючок). Выходной
сигнал триггера (0 или 1) не меняется до тех пор, пока одиночный импульс от другой схемы не переведет триггер в противоположное состояние.
Чтобы установить у триггера выходное значение, равное 1 (рис.А) :
а) На верхний вход подают 1. Это вызовет появление 1 на выходе вентиля OR, что, в свою очередь, вызовет появление 1 на выходе вентиля AND
б) Теперь наличие 1 на выходе AND удерживает вентиль OR даже после снятия 1 с верхнего входа (рис. Б).
Чтобы установить у триггера(рис. Б) выходное значение, равное 0, надо подать на нижний вход значение 1. Тогда на выходе инвертора появится значения 0, что вызовет появление 0 на входе и выходе вентиля AND, а также на входе вентиля OR и на выходе триггера.
Чтобы установить у триггера выходное значение, равное 1 (рис.А) :
а) На верхний вход подают 1. Это вызовет появление 1 на выходе вентиля OR, что, в свою очередь, вызовет появление 1 на выходе вентиля AND
б) Теперь наличие 1 на выходе AND удерживает вентиль OR даже после снятия 1 с верхнего входа (рис. Б).
Чтобы установить у триггера(рис. Б) выходное значение, равное 0, надо подать на нижний вход значение 1. Тогда на выходе инвертора появится значения 0, что вызовет появление 0 на входе и выходе вентиля AND, а также на входе вентиля OR и на выходе триггера.
А
Б
Слайд 11Величина, сохраняемая в триггере, определяется его выходным значением. Для изменения этого
значение другие схемы посылают импульсы на входы триггера.
Разрабатывая триггер вентили используют в качестве «строительных блоков». Затем триггеры используют в качестве элементов для создания более сложных схем. Таким образом, разработка общей схемы компьютера приобретает иерархическую структуру, в которой на каждом уровне в качестве абстрактных инструментов используются компоненты, созданные на предыдущих уровнях.
Главное значение триггерной схемы в том, что она является идеальным механизмом для хранения двоичных данных (битов) внутри компьютера. Триггер обеспечивает создание элементарной ячейки памяти, необходимой для хранения одного из двух знаков («0» или «1»), используемых для внутримашинного представления данных и команд.
Чаще применяется более крупная единица — байт, содержащая восемь последовательных битов - восьмиразрядное двоичное слово. Так, для того, чтобы представить любой из 256 символов, вводимых с клавиатуры компьютера, необходимо и достаточно восемь двоичных разрядов (28 = 256 бит = 1 байт).
Широко используются также более крупные производные единицы информации:
1 Килобайт (Кбайт) = 1024 байт = 210 байт,
1 Мегабайт (Мбайт) = 1024 Кбайт = 220 байт,
1 Гигабайт (Гбайт) = 1024 Мбайт = 230 байт.
1 Терабайт (Тбайт) = 1024 Гбайт = 240 байт,
1 Петабайт (Пбайт) = 1024 Тбайт = 250 байт.
Алгебра логики удобна для описания работы аппаратных средств и позволяет упростить логические функции, а, следовательно, уменьшить число элементарных логических элементов, из которых состоят основные узлы компьютера.
Разрабатывая триггер вентили используют в качестве «строительных блоков». Затем триггеры используют в качестве элементов для создания более сложных схем. Таким образом, разработка общей схемы компьютера приобретает иерархическую структуру, в которой на каждом уровне в качестве абстрактных инструментов используются компоненты, созданные на предыдущих уровнях.
Главное значение триггерной схемы в том, что она является идеальным механизмом для хранения двоичных данных (битов) внутри компьютера. Триггер обеспечивает создание элементарной ячейки памяти, необходимой для хранения одного из двух знаков («0» или «1»), используемых для внутримашинного представления данных и команд.
Чаще применяется более крупная единица — байт, содержащая восемь последовательных битов - восьмиразрядное двоичное слово. Так, для того, чтобы представить любой из 256 символов, вводимых с клавиатуры компьютера, необходимо и достаточно восемь двоичных разрядов (28 = 256 бит = 1 байт).
Широко используются также более крупные производные единицы информации:
1 Килобайт (Кбайт) = 1024 байт = 210 байт,
1 Мегабайт (Мбайт) = 1024 Кбайт = 220 байт,
1 Гигабайт (Гбайт) = 1024 Мбайт = 230 байт.
1 Терабайт (Тбайт) = 1024 Гбайт = 240 байт,
1 Петабайт (Пбайт) = 1024 Тбайт = 250 байт.
Алгебра логики удобна для описания работы аппаратных средств и позволяет упростить логические функции, а, следовательно, уменьшить число элементарных логических элементов, из которых состоят основные узлы компьютера.
Слайд 16Законов и правил логики очень много. Cамые первые, те, по отношению
к которым остальные являются производными, сформулированы Аристотелем: закон запрета противоречия, закон тождества, закон исключенного третьего, четвертый закон – достаточного основания – выдвинут немецким математиком и философом семнадцатого-восемнадцатого веков Лейбницем.
Существует три фундаментальных свойства логической мысли - определенность, последовательность и обоснованность. Они являются обязательными для мышления, когда оно занимается рассуждением. Основные законы логики отражают эти специфические черты мыслительной деятельности и в этом смысле производны от них.
Определенность означает, что любая вещь, ставшая предметом логического анализа, обязательно должна мыслиться в совокупности одних и тех же однажды выделенных признаков; они задаются при определении понятий, и не могут бесконтрольно изменяться в рамках одного и того же рассуждения.
Под последовательностью принимают то, что, приняв какое-либо положение за истинное, необходимо принимать и все вытекающие из него следствия, придерживаться их неукоснительно.
Обоснованность отражает факт взаимозависимости любых мыслей от многих других; в логике можно рассматривать только такие высказывания, которые могут быть обоснованы, выведены из других положений. Содержание обоснованности раскрывается законом достаточного основания
1. ЗАКОН ТОЖДЕСТВА. Всякая мысль тождественна самой себе, т.е. субъект рассуждений должен быть строго определен и неизменен до их окончания. Нарушением этого закона является подмена понятий (часто используется в адвокатской практике).
2. ЗАКОН НЕПРОТИВОРЕЧИЯ. Два противоположных суждения не могут быть одновременно истинны: по крайней мере одно из них ложно.
3. ЗАКОН ИСКЛЮЧЕННОГО ТРЕТЬЕГО. Истинно либо суждение, либо его отрицание ("третьего не дано").
4. ЗАКОН ДОСТАТОЧНЫХ ОСНОВАНИЙ. Для истинности всякой мысли должно быть достаточно оснований, т.е. умозаключение необходимо обосновать исходя из суждений, истинность которых уже доказана.
3.2. Объекты изучения логики.
Объектами изучения логики являются формы мышления: понятие, суждение и умозаключение.
Понятие – это мысль, в которой обобщаются отличительные свойства предметов. Т.к. язык является формой выражения мысли, то в языке термину “понятие” соответствует “слово”. Но человек не мыслит отдельными понятиями. Выражая свои мысли, он составляет слова в предложения. Предложение в языке есть суждение в мыслях.
Суждение (высказывание) – есть мысль (выраженная в форме повествовательного предложения), в которой нечто утверждается о предмете действительности, которая объективно является либо истинной, либо ложной. К числу суждений не относятся мысли, не имеющие значения истинности..
Существует три фундаментальных свойства логической мысли - определенность, последовательность и обоснованность. Они являются обязательными для мышления, когда оно занимается рассуждением. Основные законы логики отражают эти специфические черты мыслительной деятельности и в этом смысле производны от них.
Определенность означает, что любая вещь, ставшая предметом логического анализа, обязательно должна мыслиться в совокупности одних и тех же однажды выделенных признаков; они задаются при определении понятий, и не могут бесконтрольно изменяться в рамках одного и того же рассуждения.
Под последовательностью принимают то, что, приняв какое-либо положение за истинное, необходимо принимать и все вытекающие из него следствия, придерживаться их неукоснительно.
Обоснованность отражает факт взаимозависимости любых мыслей от многих других; в логике можно рассматривать только такие высказывания, которые могут быть обоснованы, выведены из других положений. Содержание обоснованности раскрывается законом достаточного основания
1. ЗАКОН ТОЖДЕСТВА. Всякая мысль тождественна самой себе, т.е. субъект рассуждений должен быть строго определен и неизменен до их окончания. Нарушением этого закона является подмена понятий (часто используется в адвокатской практике).
2. ЗАКОН НЕПРОТИВОРЕЧИЯ. Два противоположных суждения не могут быть одновременно истинны: по крайней мере одно из них ложно.
3. ЗАКОН ИСКЛЮЧЕННОГО ТРЕТЬЕГО. Истинно либо суждение, либо его отрицание ("третьего не дано").
4. ЗАКОН ДОСТАТОЧНЫХ ОСНОВАНИЙ. Для истинности всякой мысли должно быть достаточно оснований, т.е. умозаключение необходимо обосновать исходя из суждений, истинность которых уже доказана.
3.2. Объекты изучения логики.
Объектами изучения логики являются формы мышления: понятие, суждение и умозаключение.
Понятие – это мысль, в которой обобщаются отличительные свойства предметов. Т.к. язык является формой выражения мысли, то в языке термину “понятие” соответствует “слово”. Но человек не мыслит отдельными понятиями. Выражая свои мысли, он составляет слова в предложения. Предложение в языке есть суждение в мыслях.
Суждение (высказывание) – есть мысль (выраженная в форме повествовательного предложения), в которой нечто утверждается о предмете действительности, которая объективно является либо истинной, либо ложной. К числу суждений не относятся мысли, не имеющие значения истинности..
Слайд 176) Законы идемпотентности:
А ∨ А = А – отсутствие
коэффициентов;
А ∧ А = А – отсутствие степеней.
7) Законы коммутативности:
А ∨ В = В ∨ А,
А ∧ В = В ∧ А
8) Законы ассоциативности:
А ∨ (В ∨ С) = (А ∨ В) ∨ С,
А ∧ (В ∧ С) = (А ∧ В) ∧ С
9) Законы дистрибутивности:
А ∨ (В∧С) = (А∨В) ∧ (А∨С) – дизъюнкции относительно конъюнкции;
А ∧ (В∨С) = (А ∧ В) ∨ (А ∧ С) – конъюнкции относительно дизъюнкции.
10) Законы поглощения:
А ∨ А ∧ В = А
А ∧ (А ∨ В) = А
11) Законы де Моргана:
¬(А ∨ В) = ¬ А ∧¬ В – отрицание вариантов;
¬(А ∧ В) = ¬А ∨ ¬В – отрицание одновременной истинности.
Здесь в левой части тождества операция отрицания стоит над всем высказыванием. В правой части отрицание стоит над каждым из простых высказываний, но одновременно меняется операция дизъюнкция на конъюнкцию и наоборот. Пример:
«Неверно, что я знаю Pascal или Basic» тождественно тому, что «Я не знаю Pascal и не знаю Basic».
А ∧ А = А – отсутствие степеней.
7) Законы коммутативности:
А ∨ В = В ∨ А,
А ∧ В = В ∧ А
8) Законы ассоциативности:
А ∨ (В ∨ С) = (А ∨ В) ∨ С,
А ∧ (В ∧ С) = (А ∧ В) ∧ С
9) Законы дистрибутивности:
А ∨ (В∧С) = (А∨В) ∧ (А∨С) – дизъюнкции относительно конъюнкции;
А ∧ (В∨С) = (А ∧ В) ∨ (А ∧ С) – конъюнкции относительно дизъюнкции.
10) Законы поглощения:
А ∨ А ∧ В = А
А ∧ (А ∨ В) = А
11) Законы де Моргана:
¬(А ∨ В) = ¬ А ∧¬ В – отрицание вариантов;
¬(А ∧ В) = ¬А ∨ ¬В – отрицание одновременной истинности.
Здесь в левой части тождества операция отрицания стоит над всем высказыванием. В правой части отрицание стоит над каждым из простых высказываний, но одновременно меняется операция дизъюнкция на конъюнкцию и наоборот. Пример:
«Неверно, что я знаю Pascal или Basic» тождественно тому, что «Я не знаю Pascal и не знаю Basic».