- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нарушение первой предпосылки Гаусса-Маркова презентация
Содержание
- 1. Нарушение первой предпосылки Гаусса-Маркова
- 6. Гетероскедастичность случайного возмущения Нарушение предпосылок Гаусса-Маркова
- 7. ОПРЕДЕЛЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ Гетероскедастичность – это неоднородность наблюдений.
- 8. Проверка гомоскедастичности остатков Гомоскедастичность
- 9. Трехмерное изображение гомос- и гетероскедастичности Гомоскедастичность остатков Гетероскедастичность остатков
- 10. Причины гетероскедастичности Характер данных Неоднородность исследуемых объектов
- 11. Причины гетероскедастичности Причиной непостоянства дисперсии эконометрической модели часто является ее зависимость от масштаба рассматриваемых явлений.
- 12. Последствия гетероскедастичности МНК оценки параметров несмещённые Гетероскедастичность
- 13. Предварительная работа: 1. Нет ли очевидных
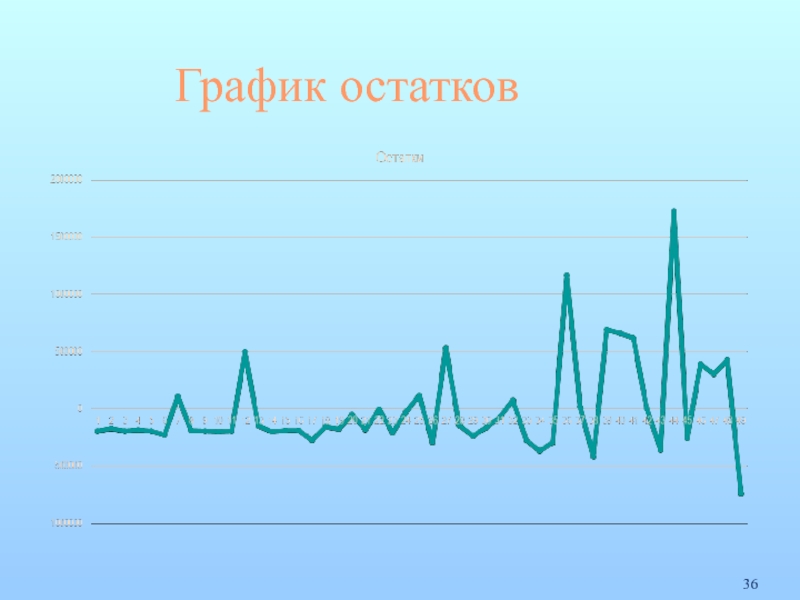
- 14. График остатков 36
- 15. Тесты: 1. Тест ранговой корреляции Спирмена.
- 16. Тест Голдфельда – Квандта Предпосылки теста: 1.
- 17. Тест Голдфельда – Квандта Алгоритм применения 1.
- 18. Тест Голдфельда – Квандта Алгоритм применения 4.
- 19. Определение критического значения F - статистики
Слайд 7ОПРЕДЕЛЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ
Гетероскедастичность – это неоднородность
наблюдений. Она характеризуется тем, что не
выполняется предпосылка
Выполнимость предпосылки 20 называется
гомоскедастичностью.
Слайд 8 Проверка гомоскедастичности остатков Гомоскедастичность – дисперсия каждого отклонения
Гетероскедастичность – разная дисперсия для различных x:
а) дисперсия остатков растет с ростом x,
б) дисперсия максимальная при средних значениях x,
в) дисперсия уменьшается с ростом x.
Слайд 9Трехмерное изображение гомос- и гетероскедастичности
Гомоскедастичность остатков Гетероскедастичность остатков
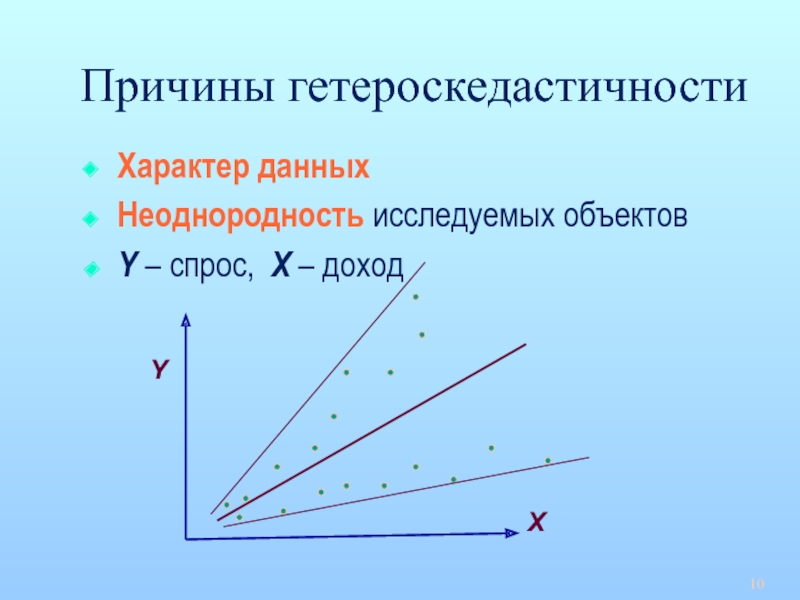
Слайд 10Причины гетероскедастичности
Характер данных
Неоднородность исследуемых объектов
Y – спрос, X – доход
Y
X
Слайд 11Причины гетероскедастичности
Причиной непостоянства дисперсии
эконометрической модели часто является ее зависимость
от масштаба рассматриваемых
Слайд 12Последствия гетероскедастичности
МНК оценки параметров несмещённые Гетероскедастичность не приводит к смещению оценок
Стандартные ошибки коэффициентов
(вычисленные в предположении.
гомоскедастичности) будут занижены. Это
приведет к завышению t-статистик и даст
неправильное (завышенное) представление о
точности оценок.
Слайд 13Предварительная работа:
1. Нет ли очевидных ошибок спецификации?
2. Можно ли содержательно предполагать
вид гетероскедастичности?
3. Рассмотрение графиков остатков:
Обнаружение гетероскедастичности
Слайд 15Тесты:
1. Тест ранговой корреляции Спирмена.
2. Тест Парка.
3. Тест Глейзера.
4. Тест Голдфелда-Квандта.
5.
6. Тест Бреуша-Пагана.
Обнаружение гетероскедастичности
Слайд 16Тест Голдфельда – Квандта
Предпосылки теста:
1. Дисперсия возмущений пропорциональна одному из регрессоров.
пропорциональны фактору пропорциональности
Z, т.е.
2. Случайный член ε имеет нормальное распределение и отсутствует автокорреляция остатков (предпосылка 30).
Слайд 17Тест Голдфельда – Квандта
Алгоритм применения
1. Выделяют фактор пропорциональности Z = Xk.
Данные
величины Z.
2. Отбрасывают среднюю треть упорядоченных
наблюдений. Для первой и последней третей
строятся две отдельные регрессии, используя ту же
спецификацию модели регрессии.
3. Количество наблюдений в этих подвыборках
должно быть одинаково. Обозначим его l.
Слайд 18Тест Голдфельда – Квандта
Алгоритм применения
4. Берутся суммы квадратов остатков для регрессий
первой трети RSS1 и последней трети RSS3. Рассчитывают
их отношение:
5. Используем F-тест для проверки гомоскедастичности.
Если статистика GQ удовлетворяет неравенству
то гипотеза гомоскедастичности остатков отвергается на
уровне значимости α.
Слайд 19Определение критического значения
F - статистики в Excel
Категория — Статистические
Функция —
Параметры функции Fраспобр:
Вероятность (уровень значимости )
Число степеней свободы 1 (v1 = m - k)
Число степеней свободы 2 (v2 = m - k)