- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование термической деградации AlGaAs гетероструктур презентация
Содержание
- 1. Моделирование термической деградации AlGaAs гетероструктур
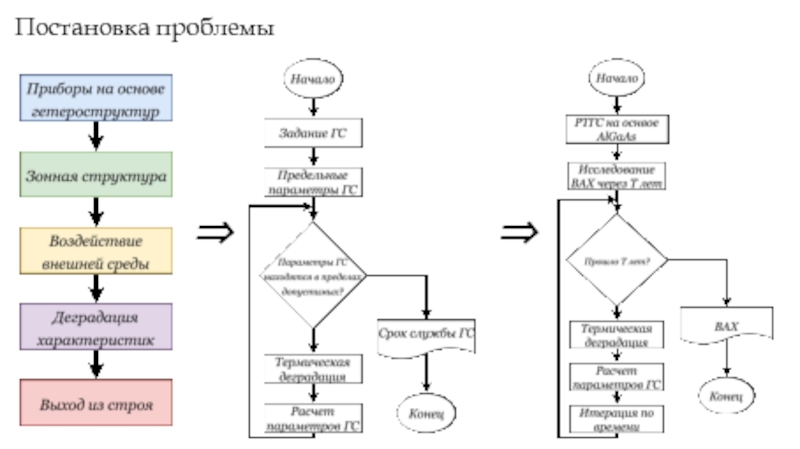
- 2. Постановка проблемы ⇒ ⇒
- 3. Цели и задачи Цель работы: ) Разработка
- 4. Численное моделирование физических процессов 0 S(x )
- 5. Численное моделирование диффузии Коэффициент диффузии постоянен: .D
- 6. Численное моделирование диффузии Диффузионное размытиеi-GaAs /i-AlxGa1−xAs/i-GaAs: DAl
- 7. Численное моделирование диффузии Коэффициент диффузии зависит от
- 8. Численное моделирование диффузии Диффузионное размытиеn +-GaAs/i-GaAs/i-AlxGa1
- 9. Численное моделирование токопереноса Формула Цу-Есаки: Численное решение
- 10. Численное моделирование токопереноса • a =
- 11. Учет самосогласованного потенциала Уравнеие Пуассона:
- 12. Исследование влияния параметров РТГС на ВАХ
- 13. Исследование влияния параметров ямы РТГС на ВАХ
- 14. Исследование влияния параметров барьеров РТГС на
- 15. Исследование влияния параметров спейсера РТГС на
- 16. Моделирование термической деградации ВАХ AlxGa1−xAs РТГС Исследуемая
- 17. Моделирование термической деградации квантовой области ND =
- 18. Моделирование термической деградации квантовой области с учетом
- 19. Заключение В ходе работы были: ) Исследована
- 20. Спасибо за внимание!
Слайд 1Моделирование термической деградации AlGaAs гетероструктур
Выполнил: студент гр. РЛ6–82 Прохоров М.Д. Руководитель:
МГТУ им. Н.Э.Баумана
Москва, 2017
Слайд 3Цели и задачи
Цель работы:
) Разработка алгоритма прогнозирования деградации слоистых гетероструктур на
Задачи работы:
) Моделирование диффузионного размытия гетероструктур на основе GaAs под дейсвтвием градиента концентрации при фиксированной температуре;
) Моделирование токопереноса через гетеростуктуру;
) Разработка алгоритма деградации ВАХ гетероструктуры на основе GaAs.
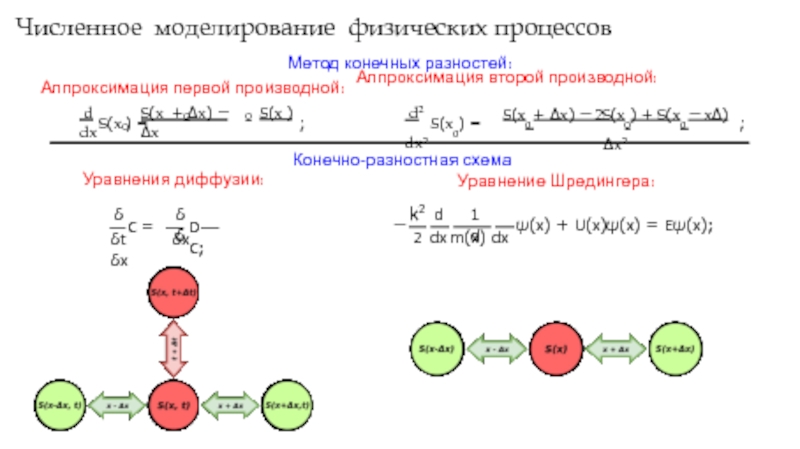
Слайд 4Численное моделирование физических процессов
0
S(x ) =
0 0
S(x )
d S(x + ∆x)
dx ∆x
;
Метод конечных разностей:
Аппроксимация первой производной: Аппроксимация второй производной:
d
2
dx2 S(x0) =
S(x0 + ∆x) − 2S(x0) + S(x0 − x∆)
∆x2
;
Уравнения диффузии:
δ δ δ
δt δx δx
C = D C;
Конечно-разностная схема
Уравнение Шредингера:
−
k2 d 1 d
2 dx m(x) dx
ψ(x) + U(x)ψ(x) = Eψ(x);
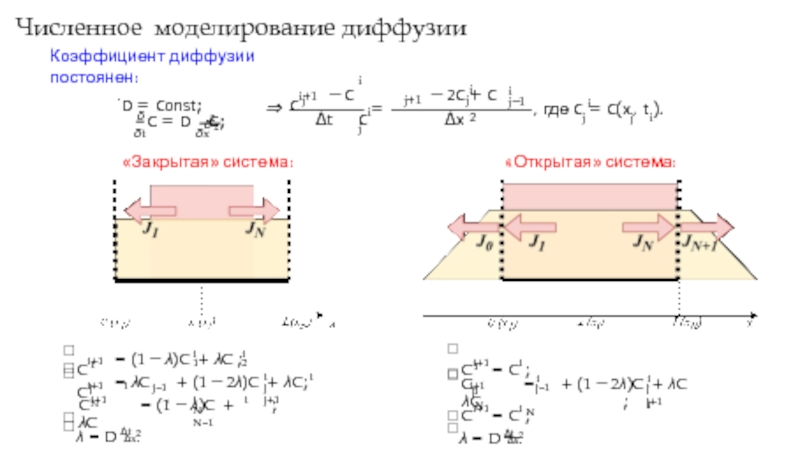
Слайд 5Численное моделирование диффузии
Коэффициент диффузии постоянен:
.D = Const;
δ2
δ
δt δx
2
C = D C;
⇒
Ci+1
j
− C
∆t
=
i Ci
j
i
j+1 j
− 2C
i j−1
∆x
2
i
, где Cj = C(xj, ti).
«Закрытая» система:
Ci+1
1
i
1
i
2
= (1 − λ)C + λC ;
j
Ci+1 i
j−1
i
i
j j+1
= λC + (1 − 2λ)C + λC ;
i+1
N
i
C = (1 − λ)C + λC
i
N N−1
;
∆x2
λ = D ∆t .
«Открытая» система:
1 1
Ci+1 = Ci ;
i+1
Cj = λC
i
j−1
i i
j j+1
+ (1 − 2λ)C + λC ;
N
N
Ci+1 = Ci ;
∆x2
λ = D ∆t .
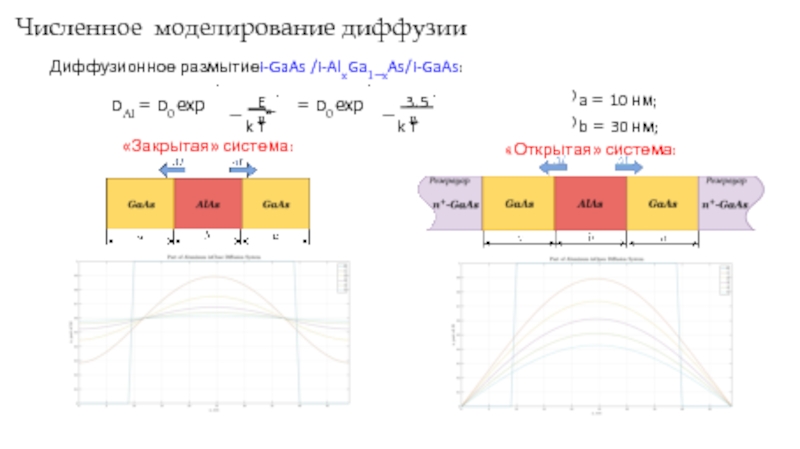
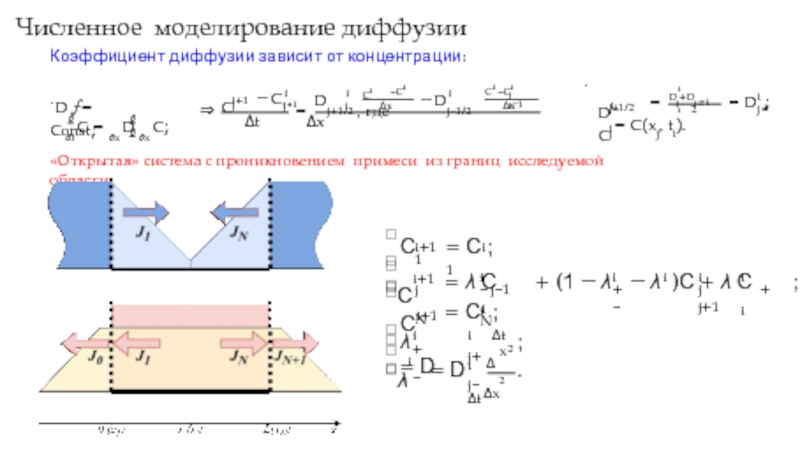
Слайд 6Численное моделирование диффузии
Диффузионное размытиеi-GaAs /i-AlxGa1−xAs/i-GaAs:
DAl = D0 exp
.
B
− k T
Ea
= D0 exp
.
B
− k T
3.5 .
«Закрытая» система:
) a = 10 нм;
) b = 30 нм;
«Открытая» система:
Слайд 7Численное моделирование диффузии
Коэффициент диффузии зависит от концентрации:
.D ƒ= Const;
δ δ δ
δt C =
⇒
Ci+1
j
− Cj
Dj+1/2
Ci
−Ci
i i j+1 j
∆x
− Dj−1/2
Ci −Ci
i j j−1
∆x
∆t ∆x
= , где
.
Di
j±1/2
=
i i
Dj+Dj±1
2
i
±
= Dj ;
Ci
j = C(xj, ti).
«Открытая» система с проникновением примеси из границ исследуемой области:
i+1
1
i
C = C ;
1
Ci+1
j
= λ C
i i
+ (1 − λ
i
i
+ −
i
− λ )C + λ C
i i
j + j+1
;
Ci+1
N
− j−1
i
= CN;
i
+
λ = D
i
∆t
j+ ∆
x
2
λ
i
−
= D
i ∆t
j− ∆x2
;
.
Слайд 8Численное моделирование диффузии
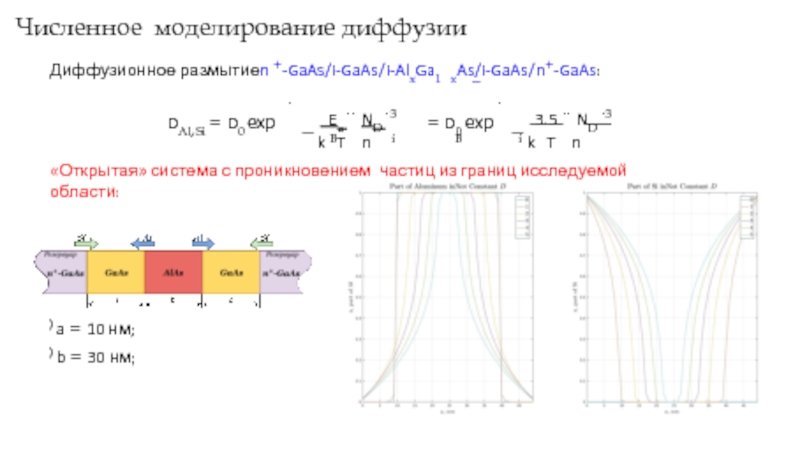
Диффузионное размытиеn +-GaAs/i-GaAs/i-AlxGa1 xAs/i-GaAs/n+-GaAs:
−
DAl,Si = D0 exp
.
− k
Ea .. ND .3
= D0 exp
.
− k T n
B i B i
3.5 .. ND .3
«Открытая» система с проникновением частиц из границ исследуемой области:
) a = 10 нм;
) b = 30 нм;
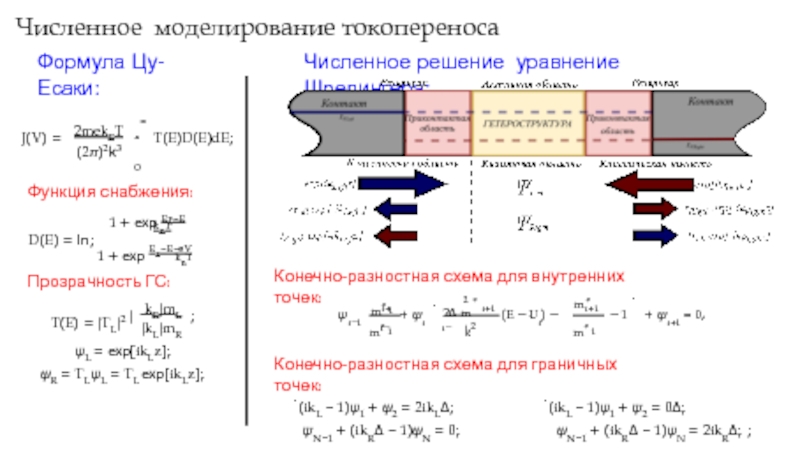
Слайд 9Численное моделирование токопереноса
Формула Цу-Есаки:
Численное решение уравнение Шредингера:
J(V) =
2mekBT
(2π)2k3
¸∞
T(E)D(E)dE;
0
Функция снабжения:
1 + exp
1 + exp EF−E−eV
kBT
D(E) = ln ;
kBT
Прозрачность ГС:
T(E) = |TL|2 |
kR|mL
|kL|mR
;
ψL = exp[ikLz];
ψR = TLψL = TL exp[ikLz];
Конечно-разностная схема для внутренних точек:
i+
m∗ 1
m∗ 1
ψi−1 + ψi
. 2∆ m
2 ∗
i+1
k2
(E − Ui) −
m
∗
i+1
i− i−
m∗ 1
− 1
.
+ ψi+1 = 0,
Конечно-разностная схема для граничных точек:
.(ikL − 1)ψ1 + ψ2 = 2ikL∆;
ψN−1 + (ikR∆ − 1)ψN = 0;
.(ikL − 1)ψ1 + ψ2 = 0∆;
ψN−1 + (ikR∆ − 1)ψN = 2ikR∆; ;
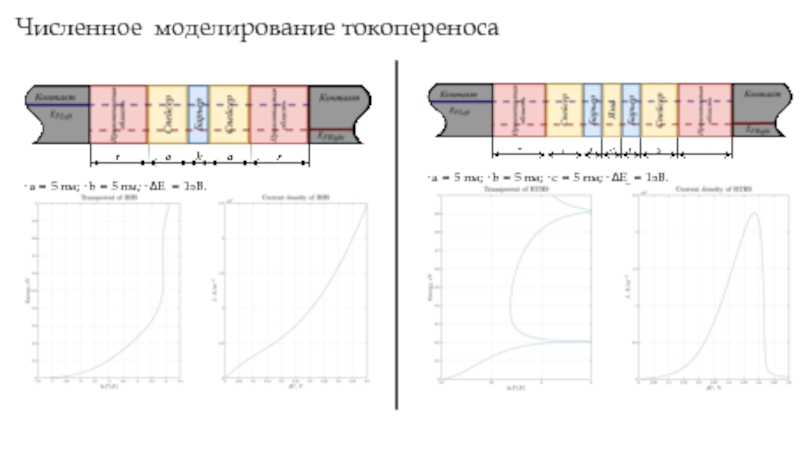
Слайд 10Численное моделирование токопереноса
• a = 5 нм; • b = 5
• a = 5 нм; • b = 5 нм; • c = 5 нм; • ∆Ec = 1эВ.
Слайд 11Учет самосогласованного потенциала
Уравнеие Пуассона:
ε(x) Vs =
d d e
dx x ε0
[n(x) − ND(x)];
Метод Гумеля:
n(x) =
21/2m3/2kBT
(2π)2k3
exp
EF(x)
kBT
VS(x)
= n0(x) exp ;
Vref
Vref =
kBT e
; n0(x) =
21/2m3/2kBT
(2π)2k3
exp
EF(x) − Ec(x)
kBT
;
nnew = nold exp
Vnew − Vold
Vref
;
Конечно-разностная схема:
d d
dx x
ε(x) Vnew =
old
exp
Vnew − Vold Vref
e . . .
n
ε0
D
.
− N (x) ;
d d
dz z
ε(z) Vnew − nold
eVnew
ε0Vref
ε0
e . .
Vref
Vold .
.
= nold 1 − − ND(z) ;
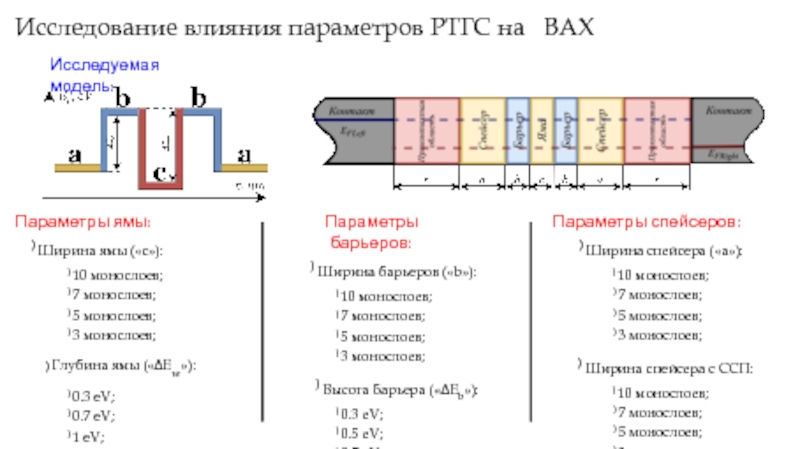
Слайд 12Исследование влияния параметров РТГС на ВАХ
Исследуемая модель:
Параметры ямы:
) Ширина ямы
) 10 монослоев;
) 7 монослоев;
) 5 монослоев;
) 3 монослоев;
) Глубина ямы («∆Ew»):
) 0.3 eV;
) 0.7 eV;
) 1 eV;
) 1.3 eV;
Параметры барьеров:
) Ширина барьеров («b»):
) 10 монослоев;
) 7 монослоев;
) 5 монослоев;
) 3 монослоев;
) Высота барьера («∆Eb»):
) 0.3 eV;
) 0.5 eV;
) 0.7 eV;
) 1 eV;
Параметры спейсеров:
) Ширина спейсера («a»):
) 10 монослоев;
) 7 монослоев;
) 5 монослоев;
) 3 монослоев;
) Ширина спейсера с ССП:
) 10 монослоев;
) 7 монослоев;
) 5 монослоев;
) 3 монослоев;
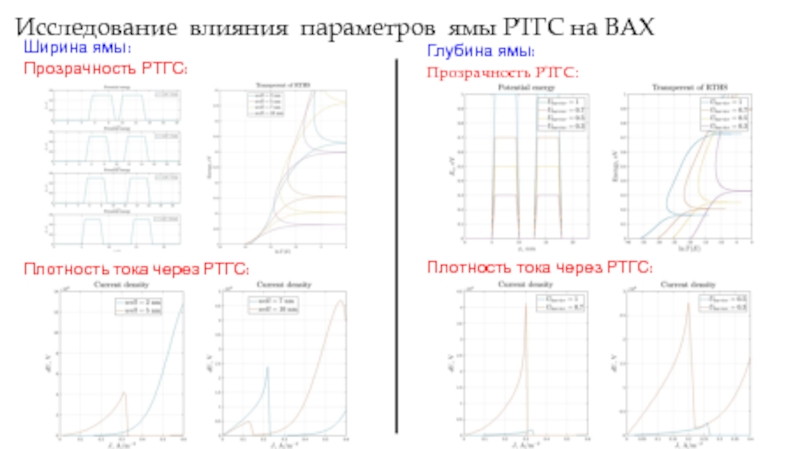
Слайд 13Исследование влияния параметров ямы РТГС на ВАХ
Ширина ямы: Прозрачность РТГС:
Плотность тока
Глубина ямы:
Прозрачность РТГС:
Плотность тока через РТГС:
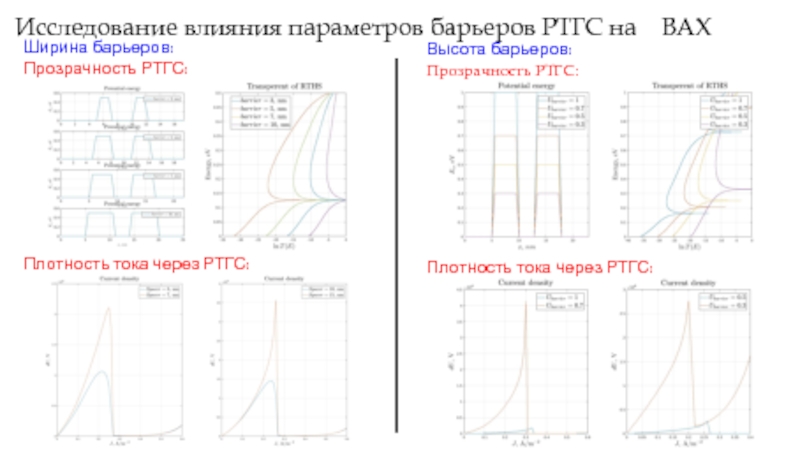
Слайд 14Исследование влияния параметров барьеров РТГС на ВАХ
Ширина барьеров: Прозрачность РТГС:
Плотность
Высота барьеров:
Прозрачность РТГС:
Плотность тока через РТГС:
Слайд 15Исследование влияния параметров спейсера РТГС на ВАХ
Ширина спейсера: Прозрачность РТГС:
Плотность
Ширина спейсера с учетом ССП: Плотность тока через РТГС:
Слайд 16Моделирование термической деградации ВАХ AlxGa1−xAs РТГС
Исследуемая модель:
Схема:
Зонная структура:
AlxGa1−xAs:
EΓ
g =
Период решетки (нм):
∆x
Ширина запрященной зоны (эВ):
,1.424 + 1.247x, x < 0.45;
1.656 + 0.215x + 0.143x2, x ≥ 0.45;
Эффективная масса в ЗП:
mΓ
eff = 0.067 + 0.083x массы электрона;
Число атомов:
N = (4.42 − 0.17x)1022 cm−3 ≈ 4.2 ∗ 1028 m−3
Параметры модели:
Размеры:
a = 10 монослоев; b = 6 монослоев; c = 6 монослоев;
Зонная структура:
∆Ec = ∆Ew = 0.6235x эВ;
Структура: n+-GaAs/i-GaAs/i-Al0.4Ga0.6As/i-GaAs/i-Al0.4Ga0.6As/i-GaAs/n+-GaAs
Параметры диффузии:
.
DAl,Si = D0 exp −
.. .
Ea ND 3;
kBT ni
Ea = 3.5эВ – энергия активации; T = 360K – температура системы;
D0 = 0.2 – предэкспоненциальный множитель;
ND – концентрация донорной примеси;
i
n – концентрация собственных
носителей заряда.
Слайд 17Моделирование термической деградации квантовой области
ND = ni = 1012m−3, T =
Диффузионное расплытие профиля:
Деградация ВАХ:
ND = 1018; ni = 1012m−3; T = 650K:
Диффузионное расплытие профиля:
Деградация ВАХ:
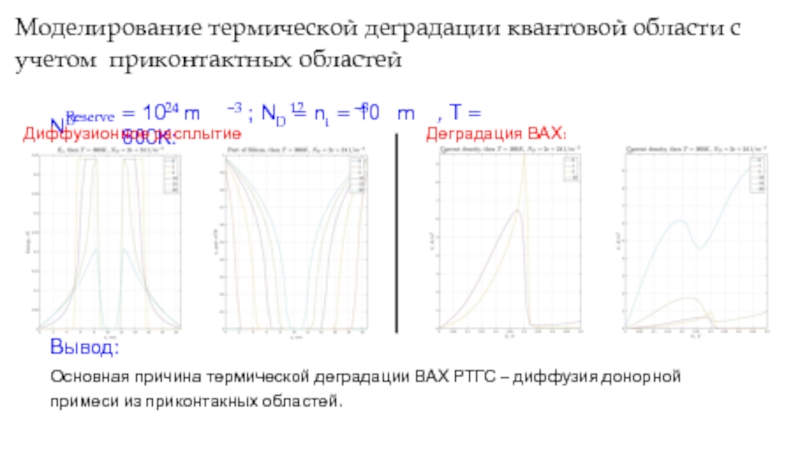
Слайд 18Моделирование термической деградации квантовой области с учетом приконтактных областей
NReserve
D
24 −3 12 −3
= 10
Диффузионное расплытие профиля:
Деградация ВАХ:
Вывод:
Основная причина термической деградации ВАХ РТГС – диффузия донорной примеси из приконтакных областей.
Слайд 19Заключение
В ходе работы были:
) Исследована модель токопереноса через гетеростуктуру с учетом
) Исследовано влияние основных параметров РТГС на ВАХ;
) Исследована модель дуффузионного расплытия гетероструктур на основе GaAs под дейсвием градиента концентрации при постоянной темпрературе;
) Исследованы различные граничные условия для дальнейшего моделирования диффузионного расплытия систем;
) Получен аглгорим моделирования термической деградации ВАХ гетероструктур.


![Учет самосогласованного потенциалаУравнеие Пуассона:ε(x) Vs =d d edx x ε0[n(x) − ND(x)];Метод Гумеля:n(x) =21/2m3/2kBT(2π)2k3expEF(x) − Ec(x) + eVs(x)kBTVS(x)= n0(x)](/img/tmb/5/432004/24b2231a1930ff36da06feb12a2b78a2-800x.jpg)