- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модели оптимального планирования презентация
Содержание
- 1. Модели оптимального планирования
- 2. Моделирование корреляционных зависимостей Виды зависимостей Функциональная Корреляционная
- 3. Корреляционная зависимость – это зависимость между
- 4. Виды задач Оказывает ли фактор В какое-либо
- 5. Раздел математической статистики, который исследует корреляционные зависимости, называется корреляционным анализом.
- 6. Оценку корреляции величин начинают с высказывания гипотезы
- 7. Мера корреляционной зависимости – это величина, которая называется коэффициентом корреляции.
- 8. ρ – характеризует величину, отражающую степень взаимосвязи
- 9. Корреляционный анализ Производительность труда – это количество
- 10. Оптимальное планирование
- 11. Оптимальное планирование. Задача оптимального планирования. Вопросы к
- 12. Объект планирования
- 13. Постановка задачи Плановые показатели Ресурсы x, y, … Зависит от плановых показателей Стратегическая цель
- 14. Оптимальным планом называется значение плановых показателей
- 15. Пример
- 16. Пример Ресурсы – транспортные средства,
- 17. Пример Плановые показатели – количество учителей и
- 18. Оптимальное планирование Плановые показатели – количество учителей
- 19. Оптимальное планирование На рыбоводческом комплексе занимаются разведением
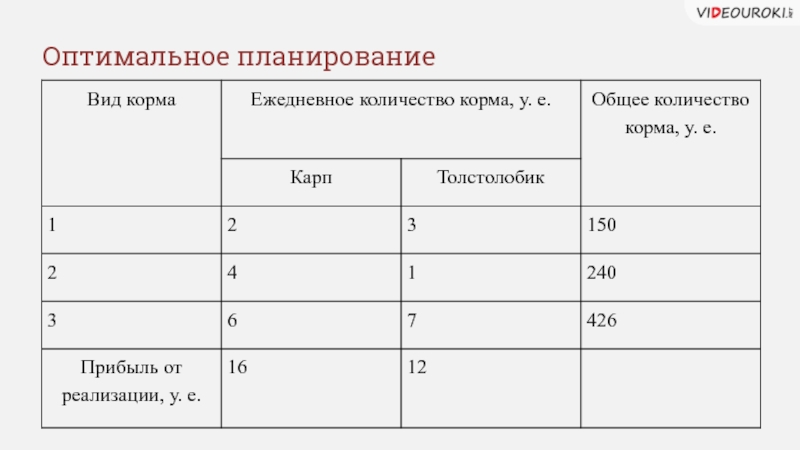
- 20. Оптимальное планирование
- 21. Оптимальное планирование х у 1 2 3 Ресурсы
- 22. Оптимальное планирование
- 23. Оптимальное планирование +
- 24. Оптимальное планирование +
- 25. Оптимальное планирование +
- 26. Математическое программирование — это раздел математики, содержащий методы решения задач оптимального планирования.
- 27. Оптимальное планирование + Линейное программирование
- 28. Линейное программирование — это раздел математического
- 29. Оптимальное планирование Мы построили модель оптимального планирования на рыбоводческом комплексе.
- 30. Функция СУММПРОИЗВ Функция СУММПРОИЗВ перемножает соответствующие
- 31. Функция СУММПРОИЗВ Функция СУММПРОИЗВ перемножает соответствующие
- 32. Оптимальное планирование Ограниченность ресурсов описывается с
Слайд 3Корреляционная зависимость – это
зависимость между величинами, каждая из
которых подвергается
разбросу.
Слайд 4Виды задач
Оказывает ли фактор В какое-либо заметное постоянное влияние на фактор
Какие из факторов В, С, D оказывают наибольшее влияние на фактор А?
Корреляционный анализ
Слайд 5Раздел математической статистики, который
исследует корреляционные зависимости,
называется корреляционным анализом.
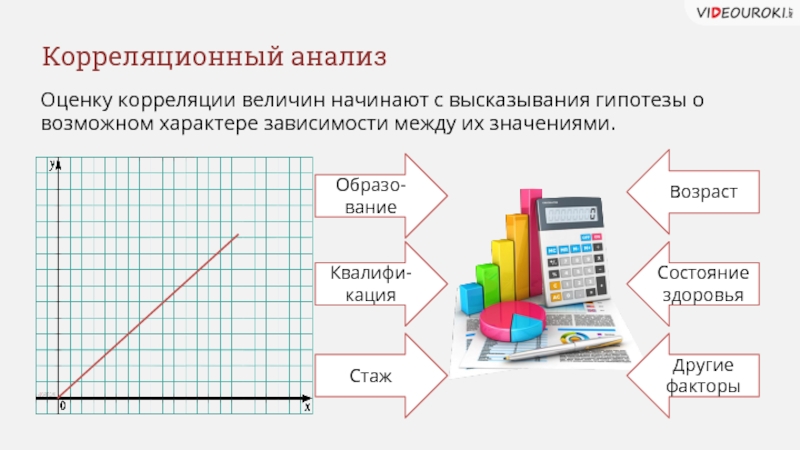
Слайд 6Оценку корреляции величин начинают с высказывания гипотезы о
возможном характере зависимости
Корреляционный анализ
Стаж
Квалифи-кация
Образо-вание
Возраст
Состояние здоровья
Другие факторы
Слайд 8ρ – характеризует величину, отражающую степень взаимосвязи двух переменных между собой;
Коэффициент
Свойства ρ:
если ρ = 0, то корреляционных связей между величинами нет. Причём если ρ близко к +1 (или –1), то корреляция сильная, а если ρ близко к 0, то слабая;
если ρ близко к +1, то это означает, что взаимосвязи типа увеличение-увеличение (или уменьшение-уменьшение);
если ρ близко к –1, то это означает, что взаимосвязи типа увеличение-уменьшение (или уменьшение-увеличение).
Слайд 9Корреляционный анализ
Производительность труда – это количество продукции, выпущенной работниками за единицу
Энерговооружённость труда – это количество всех видов энергии (электрической, тепловой и других), приходящееся на какую-либо производственную единицу.
Фактор А – производитель-ность труда
Фактор В – энерговооружён-ность труда
Корреляционная зависимость
Слайд 11Оптимальное планирование. Задача оптимального планирования.
Вопросы к изучению
Плановые показатели, ресурсы и цели.
Математическое
Слайд 13Постановка задачи
Плановые показатели
Ресурсы
x, y, …
Зависит от плановых показателей
Стратегическая цель
Слайд 14Оптимальным планом называется
значение плановых показателей при
достижении стратегической цели с
ограниченности ресурсов.
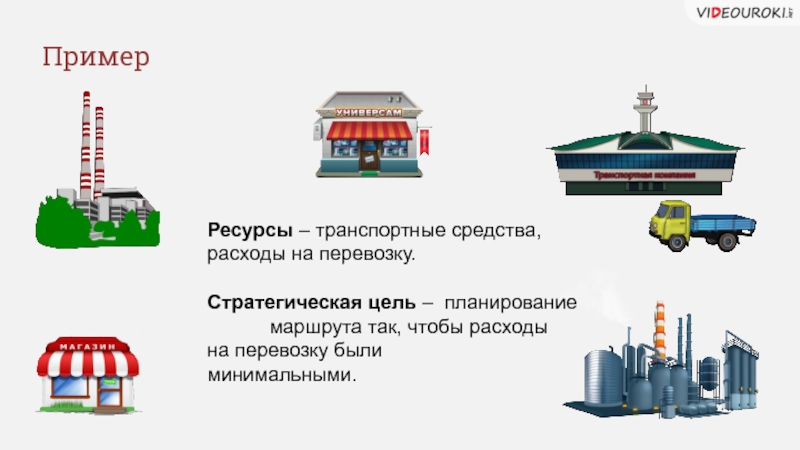
Слайд 16Пример
Ресурсы – транспортные средства, расходы на перевозку.
Стратегическая цель –
Слайд 17Пример
Плановые показатели – количество учителей и учащихся.
Основные ресурсы – объём
Стратегическая цель – образование и воспитание школьников.
Количественная мера – повышение среднего балла успеваемости.
Слайд 18Оптимальное планирование
Плановые показатели – количество учителей и учащихся.
Основные ресурсы –
Стратегическая цель – образование и воспитание школьников.
Количественная мера – повышение среднего балла успеваемости.
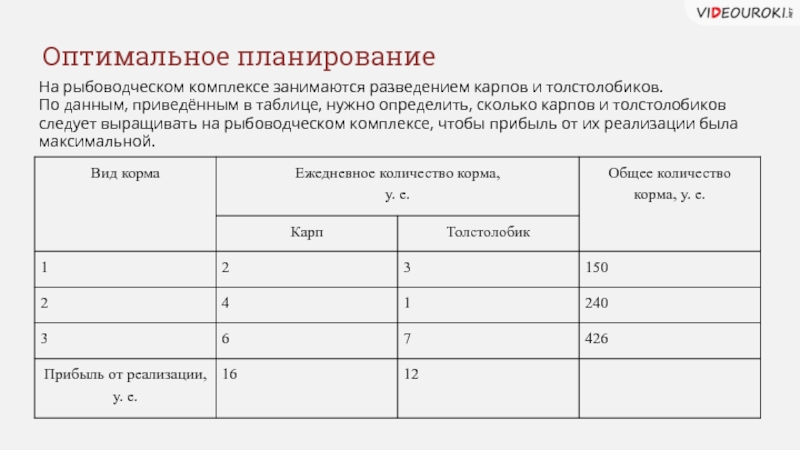
Слайд 19Оптимальное планирование
На рыбоводческом комплексе занимаются разведением карпов и толстолобиков.
По данным,
следует выращивать на рыбоводческом комплексе, чтобы прибыль от их реализации была
максимальной.
Слайд 24Оптимальное планирование
+
Цель рыбоводческого комплекса – получение максимальной выручки от продажи рыбы.
Слайд 25Оптимальное планирование
+
Целевая функция
Требуется найти значения плановых показателей х и у, которые
удовлетворять данной системе неравенств и придавать максимальное
значение целевой функции.
Математическая модель задачи оптимального планирования для рыбоводческого комплекса
Слайд 26Математическое программирование — это
раздел математики, содержащий методы
решения задач оптимального
планирования.
Слайд 28Линейное программирование — это раздел
математического программирования, решающий
задачи оптимального планирования
целевой функцией.
Слайд 29Оптимальное планирование
Мы построили модель
оптимального планирования
на рыбоводческом комплексе.
Слайд 30Функция СУММПРОИЗВ
Функция СУММПРОИЗВ перемножает соответствующие элементы заданных списков, а затем
Количество ячеек списка 1 = Количество ячеек списка 2
=СУММПРОИЗВ(диапазон ячеек1;диапазон ячеек2)
Слайд 31Функция СУММПРОИЗВ
Функция СУММПРОИЗВ перемножает соответствующие элементы заданных списков, а затем
Слайд 32Оптимальное планирование
Ограниченность ресурсов описывается с помощью
Цель
это определение значений плановых показателей
системы неравенств, системы равенств, смешанной системы.
описывается функцией, для которой требуется найти минимум или максимум.
Microsoft Excel
имеет специальное средство Поиск решения для решения задач оптимального планирования.
Модели оптимального планирования