- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическое и имитационное моделирование презентация
Содержание
- 1. Математическое и имитационное моделирование
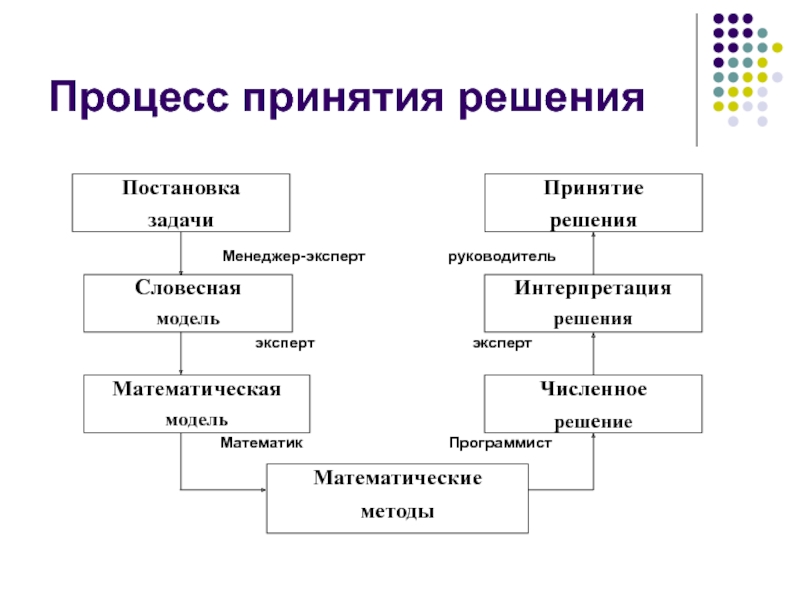
- 2. Процесс принятия решения
- 3. Выдающиеся ученые Леонид Витальевич Канторович Джордж
- 4. Моделирование Моделирование – общенаучный метод исследования, который
- 5. Модель Модель – аналог оригинала, отражающий его
- 6. Определение модели Модель — объект или описание
- 7. Требования к моделям: Универсальность - полнота отображения
- 8. Требования к моделям: Точность - степень совпадения
- 9. Цели моделирования Изучение структуры объектов (явлений) и
- 10. Моделирование Проблемам моделирования посвящено огромное число работ,
- 11. Источники Бережная Е.В. Математические методы моделирования экономических
- 12. Классификация моделей: По способу отображения действительности :
- 13. II. С учетом фактора времени: Статические
- 14. III. По области использования: учебные; опытные; игровые; научно-технические; имитационные.
- 15. IV. По области знаний: математические; химические; физические; экономические; географические и т.д.
- 16. V. По способу реализации: Компьютерные структурно-функциональные,
- 17. Информационная модель – это модель, содержащая
- 18. V. По способу представления
- 19. Классы моделей К началу XXI века сформировались 4 класса моделей Аналитические (математические), Статистические, Имитационные, Информационные.
- 20. Классы моделей
- 21. Аналитический подход к моделированию Любая модель строится
- 22. Аналитический подход к моделированию Любая модель строится
- 23. Аналитический подход к моделированию Движение от модели
- 24. Информационный подход к моделированию При информационном
- 25. Цели аналитических моделей анализ динамики на основе
- 26. Аналитические модели Характер взаимосвязей: детерминированный (т.е. не
- 27. Математические модели в экономике отражают с
- 28. Математические модели в экономике отражают с
- 29. Аналитические модели Основные предположения для построения модели
- 30. Оптимизационные математические модели Определить х, такое, что
- 31. Линейное программирование — это математическая дисциплина, посвященная
- 32. Постановка задачи линейного программирования Максимизировать (минимизировать) функцию при ограничениях
- 33. Постановка задачи линейного программирования Найти переменные задачи
- 34. Постановка задачи линейного программирования Множество допустимых решений
- 35. Каноническая форма задачи ЛП
- 36. Построение математической модели задачи ЛП 1 этап
- 37. Пример планирования производства или определение оптимального ассортимента
- 38. Какое количество продукции каждого вида должно производить
- 39. Построение матем. модели 1. Цель - максимизация
- 40. Методы решения Геометрический (графический) метод Для решения
- 41. Алгоритм решения 1. Построить прямые, соответствующие ограничениям.
- 42. Алгоритм решения 4. Определить направление возрастания (убывания)
- 43. Решение примера
- 45. Имитационное моделирование Примеры
- 46. Имитационное моделирование - численный метод проведения
- 47. Имитационная модель - это компьютерная программа,
- 48. Модели динамики народонаселения модели роста численности популяции.
- 49. Модель Мальтуса Конечно-разностное уравнение динамики численности населения:
- 51. Модель Мальтуса Описывает неограниченный, экспоненциальный рост человечества.
- 52. Модель роста народонаселения Однако, экспоненциальный рост не
- 53. Логистическая модель роста народонаселения Логистическая модель роста
- 54. Модель Ферхюльста Конечно-разностное уравнение динамики численности
- 56. Модель Ферхюльста График этого уравнения называется логистической
- 57. Модель Ферхюльста Таким образом, система в данном
- 58. Примеры применения моделей в истории Другими примерами
- 59. Примеры применения моделей в истории Важно, что
- 60. Примеры моделей Если динамических переменных больше одной,
- 61. Примеры моделей Большую известность приобрели работы
- 62. Примеры моделей Модель Лотки-Вольтерра была использована В.Вайдлихом
Процесс принятия решения
Слайд 3Выдающиеся ученые
Леонид Витальевич Канторович
Джордж Данциг
Ричард Эрнст Беллман
Василий Васильевич Леонтьев
Джорж фон
Нейман
Слайд 4Моделирование
Моделирование – общенаучный метод исследования, который широко используется не только в
естественных, но и в социально-гуманитарных науках.
Моделирование – процесс построения моделей для исследования и изучения объектов, процессов, явлений.
Моделирование – процесс построения моделей для исследования и изучения объектов, процессов, явлений.
Слайд 5Модель
Модель – аналог оригинала, отражающий его существенные признаки в соответствии с
заданной целью моделирования.
Слайд 6Определение модели
Модель — объект или описание объекта, системы для замещения (при
определенных условиях, предположениях, гипотезах) одной системы (то есть оригинала) другой системой для лучшего изучения оригинала или воспроизведения каких-либо его свойств, благодаря чему изучение модели позволяет получить новую информацию об «оригинале».
Слайд 7Требования к моделям:
Универсальность - полнота отображения моделью изучаемых свойств реального объекта,
применимость модели к анализу ряда однотипных систем.
Адекватность - способность отражать нужные существенные свойства объекта с погрешностью не выше заданной.
Адекватность - способность отражать нужные существенные свойства объекта с погрешностью не выше заданной.
Слайд 8Требования к моделям:
Точность - степень совпадения значений характеристик реального объекта и
значения этих характеристик, полученных с помощью моделей.
Экономичность - затраты на реализацию и эксплуатация не должны превышать выгоду от использования модели.
Экономичность - затраты на реализацию и эксплуатация не должны превышать выгоду от использования модели.
Слайд 9Цели моделирования
Изучение структуры объектов (явлений) и их свойств и проведение экспериментов;
Проектирование и управление;
Анализ альтернатив развития исследуемых объектов и процессов и выбор оптимального решения;
Исследование возможного поведения изучаемого явления (или класса явлений) по построенной математической модели;
Прогнозирование поведения объектов.
Слайд 10Моделирование
Проблемам моделирования посвящено огромное число работ, в которых вводятся десятки и
сотни определений понятия "модель", классификаций моделей, типов математического моделирования.
Слайд 11Источники
Бережная Е.В. Математические методы моделирования экономических систем-М.: Финансы и статистика, 2006.
Хемди
А. Таха Введение в исследование операций. – М.: «Вильямс», 2007.
Орлова И.В. Экономико-математические методы и модели. – М.: «Финанстатинформ», 2000.
Шелобаев С.И. Математические методы и модели в экономике, финансах, бизнесе - М.:ЮНИТИ-ДАНА, 2001.
Кремер Н.Ш., Исследование операций в экономике., 2007.
Орлова И.В. Экономико-математические методы и модели. – М.: «Финанстатинформ», 2000.
Шелобаев С.И. Математические методы и модели в экономике, финансах, бизнесе - М.:ЮНИТИ-ДАНА, 2001.
Кремер Н.Ш., Исследование операций в экономике., 2007.
Слайд 12Классификация моделей:
По способу отображения действительности :
Эвристические
Натурные (материальные)
Математические - формализуемые, то есть
представляют собой совокупность взаимосвязанных математических и формально-логических выражений, как правило, отображающих реальные процессы и явления.
Слайд 13II. С учетом фактора времени:
Статические – модели, описывающие состояние системы в
определенный момент времени без учета происходящих с ним изменений (единовременный срез информации по данному объекту).
Динамические – модели, описывающие процессы изменения и развития системы (изменения объекта во времени).
Динамические – модели, описывающие процессы изменения и развития системы (изменения объекта во времени).
Слайд 15IV. По области знаний:
математические;
химические;
физические;
экономические;
географические и т.д.
Слайд 16V. По способу реализации:
Компьютерные
структурно-функциональные, которые представляют собой условный образ объекта,
описанный с помощью компьютерных технологий;
имитационные, представляющие собой программу или комплекс программ, позволяющий воспроизводить процессы функционирования объекта в разных условиях.
некомпьютерные
имитационные, представляющие собой программу или комплекс программ, позволяющий воспроизводить процессы функционирования объекта в разных условиях.
некомпьютерные
Слайд 17
Информационная модель – это модель, содержащая целенаправленно отобранную и представленную в
некоторой форме наиболее существенную информацию об объекте.
Слайд 19Классы моделей
К началу XXI века сформировались 4 класса моделей
Аналитические (математические),
Статистические,
Имитационные,
Информационные.
Слайд 21Аналитический подход к моделированию
Любая модель строится и исследуется при определенных допущениях,
гипотезах. Делается это обычно с помощью математических методов.
Результаты получаются путем решения систем уравнений либо аналитически (в общем виде), либо численно (с помощью компьютера).
Результаты получаются путем решения систем уравнений либо аналитически (в общем виде), либо численно (с помощью компьютера).
Слайд 22Аналитический подход к моделированию
Любая модель строится и исследуется при определенных допущениях,
гипотезах. Делается это обычно с помощью математических методов.
Результаты получаются путем решения систем уравнений либо аналитически (в общем виде), либо численно (с помощью компьютера).
Результаты получаются путем решения систем уравнений либо аналитически (в общем виде), либо численно (с помощью компьютера).
Слайд 23Аналитический подход к моделированию
Движение от модели к результату:
При аналитическом подходе не
модель «подстраивается» под действительность, а мы пытаемся подобрать существующую аналитическую модель таким образом, чтобы она адекватно отражала реальность.
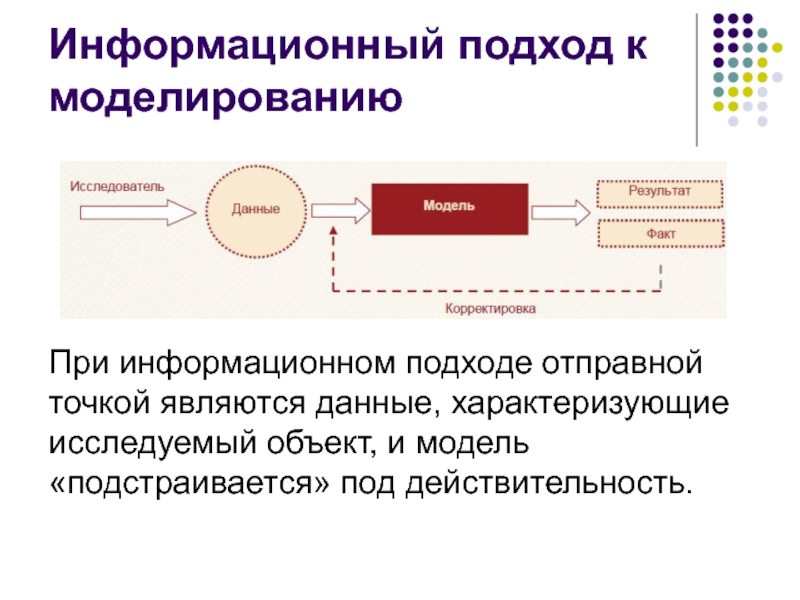
Слайд 24Информационный подход к моделированию
При информационном подходе отправной точкой являются данные, характеризующие
исследуемый объект, и модель «подстраивается» под действительность.
Слайд 25Цели аналитических моделей
анализ динамики на основе теоретических предположений о связях между
переменными,
определение некоторого желаемого (максимального или минимального) значения целевой функции путем подбора соответствующих значений входных переменных. Верификация модели возможна статистическими методами.
Дедуктивный характер модели: модели выводятся из теории.
определение некоторого желаемого (максимального или минимального) значения целевой функции путем подбора соответствующих значений входных переменных. Верификация модели возможна статистическими методами.
Дедуктивный характер модели: модели выводятся из теории.
Слайд 26Аналитические модели
Характер взаимосвязей: детерминированный (т.е. не статистический).
Требования к данным: для
верификации и подтверждения надежности модели можно использовать данные разного качества.
Параметры модели либо задаются a priori, либо выводятся из исходных данных с помощью статистических методов.
Параметры модели либо задаются a priori, либо выводятся из исходных данных с помощью статистических методов.
Слайд 27Математические модели в экономике
отражают с помощью математических соотношений основные свойства
экономических процессов и явлений
ЭТАПЫ:
Постановка экономической проблемы и ее качественный анализ
Формализация модели
Идентификация модели
Подготовка исходной информации
Численное решение
Верификация
Анализ полученных результатов
ЭТАПЫ:
Постановка экономической проблемы и ее качественный анализ
Формализация модели
Идентификация модели
Подготовка исходной информации
Численное решение
Верификация
Анализ полученных результатов
Слайд 28Математические модели в экономике
отражают с помощью математических соотношений основные свойства
экономических процессов и явлений
ЭТАПЫ:
Постановка экономической проблемы и ее качественный анализ
Формализация модели
Идентификация модели
Подготовка исходной информации
Численное решение
Верификация
Анализ полученных результатов
ЭТАПЫ:
Постановка экономической проблемы и ее качественный анализ
Формализация модели
Идентификация модели
Подготовка исходной информации
Численное решение
Верификация
Анализ полученных результатов
Слайд 29Аналитические модели
Основные предположения для построения модели строятся на упрощенном представлении о
переменных и связях между ними.
Ограничения:
малое число уравнений;
малое число переменных;
обратные связи трудны для исследования;
простые формы динамических связей.
Ограничения:
малое число уравнений;
малое число переменных;
обратные связи трудны для исследования;
простые формы динамических связей.
Слайд 30Оптимизационные математические модели
Определить х, такое, что при х∈Х значение F(x) достигает
максимального или минимального значения или коротко:
F(x)→min (max)
x - оптимальное решение (оптимальная стратегия);
X- допустимое множество (варианты стратегий);
F(x)- критерий оптимизации (целевая функция).
F(x)→min (max)
x - оптимальное решение (оптимальная стратегия);
X- допустимое множество (варианты стратегий);
F(x)- критерий оптимизации (целевая функция).
Слайд 31Линейное программирование
— это математическая дисциплина, посвященная теории и методам решения задач
об экстремумах линейных функций на множествах, задаваемых системами линейных неравенств и равенств.
Слайд 32Постановка задачи линейного программирования
Максимизировать (минимизировать) функцию
при ограничениях
Слайд 33Постановка задачи линейного программирования
Найти переменные задачи х1, х2,…,хn, которые обеспечат экстремум
ЦФ
f(х1, х2,…,хn) и удовлетворяют системе ограничений
Допустимое решение (план) задачи ЛП- это вектор Х=(х1, х2,…,хn), удовлетворяющий системе ограничений условию неотрицательности.
f(х1, х2,…,хn) и удовлетворяют системе ограничений
Допустимое решение (план) задачи ЛП- это вектор Х=(х1, х2,…,хn), удовлетворяющий системе ограничений условию неотрицательности.
Слайд 34Постановка задачи линейного программирования
Множество допустимых решений задачи образует область допустимых решений
Оптимальным
решением (оптим. планом) задачи ЛП называется допустимое решение, при котором ЦФ достигает экстремума.
Слайд 36Построение математической модели задачи ЛП
1 этап – формирование цели
2 этап –
определение параметров модели
Параметрами являются все числовые данные, приведенные в условии задачи
3 этап – формирование управляющих переменных, изменяя значение которых можно приближаться к поставленной цели.
4 этап – записать формулами ЦФ и систему ограничений
Параметрами являются все числовые данные, приведенные в условии задачи
3 этап – формирование управляющих переменных, изменяя значение которых можно приближаться к поставленной цели.
4 этап – записать формулами ЦФ и систему ограничений
Слайд 37Пример планирования производства или определение оптимального ассортимента продукции
Предприятие изготавливает два
вида продукции – П1 и П2, которая поступает в оптовую продажу. Для производства продукции используется два вида сырья – А и В. Максимально возможные запасы сырья в сутки составляют 9 и 13 единиц соответственно. Расход сырья на единицу продукции вида П1 и вида П2 дан в таблице:
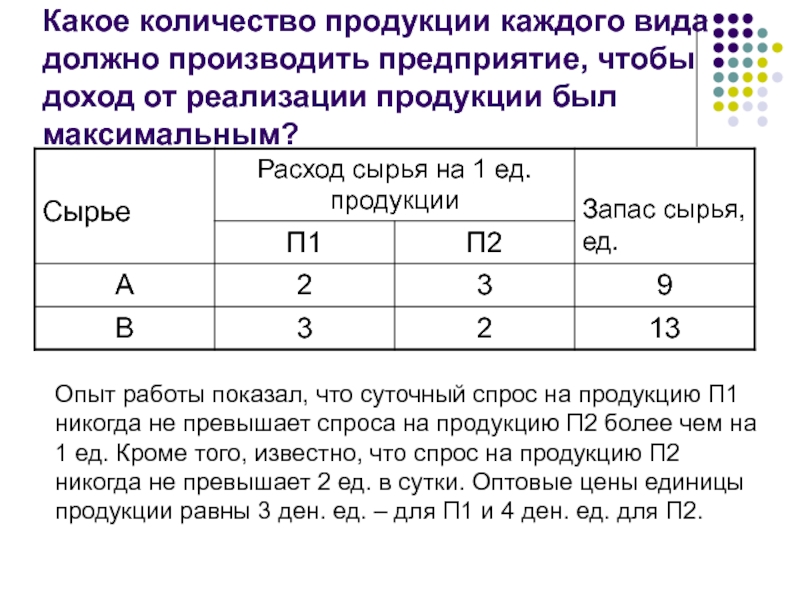
Слайд 38Какое количество продукции каждого вида должно производить предприятие, чтобы доход от
реализации продукции был максимальным?
Опыт работы показал, что суточный спрос на продукцию П1 никогда не превышает спроса на продукцию П2 более чем на 1 ед. Кроме того, известно, что спрос на продукцию П2 никогда не превышает 2 ед. в сутки. Оптовые цены единицы продукции равны 3 ден. ед. – для П1 и 4 ден. ед. для П2.
Слайд 39Построение матем. модели
1. Цель - максимизация дохода
2. Параметры – расход сырья,
запас сырья, оптовые цены продукции, цифры ограничения спроса
3. Управляющие переменные – х1 и х2 – план выпуска продукции
4. Ограничения: - производство ограничено имеющимися в распоряжении предприятия сырьем каждого вида и спросом на данную продукцию
3. Управляющие переменные – х1 и х2 – план выпуска продукции
4. Ограничения: - производство ограничено имеющимися в распоряжении предприятия сырьем каждого вида и спросом на данную продукцию
Слайд 40Методы решения
Геометрический (графический) метод
Для решения задач с двумя переменными и
задач со
многими переменными при условии, что в их канонической записи содержится не более двух свободных переменных.
Симплексный метод
Симплексный метод
Слайд 41Алгоритм решения
1. Построить прямые, соответствующие ограничениям.
2. Определить области, в которых выполняются
ограничения задачи. Для этого выбрать произвольную точку и подставить ее координаты в первую часть одного из неравенств. Если неравенство верно, то искомая полуплоскость находится с той же стороны от прямой, что и точка, в противном случае искомая полуплоскость лежит с противоположной стороны от прямой. Эти действия последовательно выполняются для всех неравенств (ограничений).
3. Определить многоугольник решений, как область пересечения m полуплоскостей, соответствующих m ограничениям задачи.
3. Определить многоугольник решений, как область пересечения m полуплоскостей, соответствующих m ограничениям задачи.
Слайд 42Алгоритм решения
4. Определить направление возрастания (убывания) целевой функции:
построить вектор-нормаль . Его
направление показывает направление возрастание функции, в противоположном направлении функция убывает.
5. Определяют граничную точку или точки области допустимых решений, в которых целевая функция принимает максимальное или минимальное значение
6. Вычисляют значение найденной точки, решая совместно уравнения, задающие прямые, на пересечении которых находится эта точка, или выявляя уравнение граничной прямой области допустимых решений, с которой совпадает линия уровня целевой функции.
5. Определяют граничную точку или точки области допустимых решений, в которых целевая функция принимает максимальное или минимальное значение
6. Вычисляют значение найденной точки, решая совместно уравнения, задающие прямые, на пересечении которых находится эта точка, или выявляя уравнение граничной прямой области допустимых решений, с которой совпадает линия уровня целевой функции.
Слайд 46Имитационное моделирование
- численный метод проведения на ЭВМ вычислительных экспериментов с
математическими моделями, имитирующими поведение реальных объектов, процессов и систем во времени в течение заданного периода, в результате чего можно получить нужную информацию об объектах окружающего мира, не обращаясь непосредственно к этим объектам, явлениям и процессам.
Слайд 47Имитационная модель
- это компьютерная программа, позволяющая воспроизводить на ЭВМ поведение
отдельных элементов системы и связей между ними в течение заданного времени моделирования.
Имитационные (вычислительные) эксперименты
- это эксперименты с ИМ.
Имитационные (вычислительные) эксперименты
- это эксперименты с ИМ.
Слайд 48Модели динамики народонаселения
модели роста численности популяции. Простейшая модель такого рода (закон
экспоненциального роста) была использована в XIX веке Т. Мальтусом.
Недостаток: модель не учитывала, что общий объем жизненных ресурсов накладывает естественные ограничения на динамику развития процесса.
Недостаток: модель не учитывала, что общий объем жизненных ресурсов накладывает естественные ограничения на динамику развития процесса.
Слайд 49Модель Мальтуса
Конечно-разностное уравнение динамики численности населения:
Ni+1=Ni + rNi – mNi
или
Ni+1=Ni
+ (r – m)Ni
где разность (r – m) – коэффициент прироста.
Если этот коэффициент больше нуля (рождаемость выше смертности), население растет, если меньше нуля – убывает.
Если этот коэффициент больше нуля (рождаемость выше смертности), население растет, если меньше нуля – убывает.
Слайд 51Модель Мальтуса
Описывает неограниченный, экспоненциальный рост человечества.
В результате был получен весьма неблагоприятный
прогноз, связанный с невозможностью обеспечить жизненными ресурсами неограниченно растущее население.
Слайд 52Модель роста народонаселения
Однако, экспоненциальный рост не может продолжаться долго. Естественные ограничения
на него накладывает внешняя среда, ресурсы которой не безграничны.
В простейшем случае можно предположить, что коэффициент прироста не является постоянным, а убывает с течением времени, по мере роста населения.
В простейшем случае можно предположить, что коэффициент прироста не является постоянным, а убывает с течением времени, по мере роста населения.
Слайд 53Логистическая модель роста народонаселения
Логистическая модель роста народонаселения была предложена П. Ферхюльстом
(в
этой модели предполагается, что прирост численности в каждый момент прямо пропорционален достигнутой численности и обратно пропорционален ее квадрату).
Слайд 54Модель Ферхюльста
Конечно-разностное уравнение динамики численности населения:
Ni+1 = Ni +rNi –
mNi – bNi2
Решение этого уравнения приводит к тому, что численность населения не растет неограниченно, а стремится к некоторой предельной величине.
Решение этого уравнения приводит к тому, что численность населения не растет неограниченно, а стремится к некоторой предельной величине.
Слайд 56Модель Ферхюльста
График этого уравнения называется логистической кривой.
Таким образом, система в данном
случае имеет устойчивое (стационарное) состояние; этому состоянию соответствует прирост населения, равный нулю (рождаемость уравновешивается смертностью).
Слайд 57Модель Ферхюльста
Таким образом, система в данном случае имеет устойчивое (стационарное) состояние;
этому состоянию соответствует прирост населения, равный нулю (рождаемость уравновешивается смертностью).
Слайд 58Примеры применения моделей в истории
Другими примерами математического моделирования для изучения сложных
социальных систем могут служить:
применение модели клеточных автоматов (для изучения электорального поведения);
теоретико-игровые модели (для изучения конфликтов, например, Карибского кризиса 1962 г.) и др.
применение модели клеточных автоматов (для изучения электорального поведения);
теоретико-игровые модели (для изучения конфликтов, например, Карибского кризиса 1962 г.) и др.
Слайд 59Примеры применения моделей в истории
Важно, что модели позволяют не только углубить
понимание сложных, развивающихся систем, но и прогнозировать их развитие, например:
модель Форрестера, имитирующая развитие американской экономики и демонстрирующая наличие коротких и длинных циклов (развитие этой модели касалось уже глобальных процессов);
модель Н. Моисеева для анализа последствий ядерной войны (эффект "ядерной зимы").
модель Форрестера, имитирующая развитие американской экономики и демонстрирующая наличие коротких и длинных циклов (развитие этой модели касалось уже глобальных процессов);
модель Н. Моисеева для анализа последствий ядерной войны (эффект "ядерной зимы").
Слайд 60Примеры моделей
Если динамических переменных больше одной, тогда и уравнений (дифференциальных или
разностных) должно быть несколько, т.е. это система уравнений.
В качестве примера системы двух уравнений укажем известную модель Лотки-Вольтерра (в биологии известна как модель "хищник-жертва", в политологии – как модель "народ-правительство", в истории – как модель "бароны и крестьяне").
В качестве примера системы двух уравнений укажем известную модель Лотки-Вольтерра (в биологии известна как модель "хищник-жертва", в политологии – как модель "народ-правительство", в истории – как модель "бароны и крестьяне").
Слайд 61Примеры моделей
Большую известность приобрели работы немецкого ученого В. Вайдлиха. Он разработал систему
моделей изучения динамики социально-экономических и политических факторов (производство и потребление товаров, инвестиции и т.п.)
Слайд 62Примеры моделей
Модель Лотки-Вольтерра была использована В.Вайдлихом для изучения отношений между "народом"
и "правительством" (или, например, парламентом и правительством). Одной переменной в этой модели является степень силы правительства, а другой переменной – степень политического влияния народа (парламента).
