- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические основы моделирования сетей связи. Основные понятия моделирования презентация
Содержание
- 1. Математические основы моделирования сетей связи. Основные понятия моделирования
- 2. Основные понятия моделирования Моделирование замещение исследуемого объекта-оригинала
- 3. Основные этапы моделирования: 1) Разработка модели;
- 4. Стадии построения модели: 1. мысленная модель;
- 5. Концептуальная модель (КМ) СМ, при формулировании
- 6. Методы моделирования Математическое моделирование исследование явлений
- 7. Этапы математического моделирования 1) - постановка задачи;
- 8. Виды ММ : аналитическая
- 9. Построение моделей сети связи Решение задач, связанных
- 10. 3. Технология обслуживания: - метод коммутации;
- 11. ММ сетей связи: 1. Первичные сети.
- 12. Классификация задач проектирования сетей связи (СС)
- 13. Что такое граф? Граф G задаётся
- 14. 1) Простой граф; 2) Мультиграф; 3) Псевдограф;
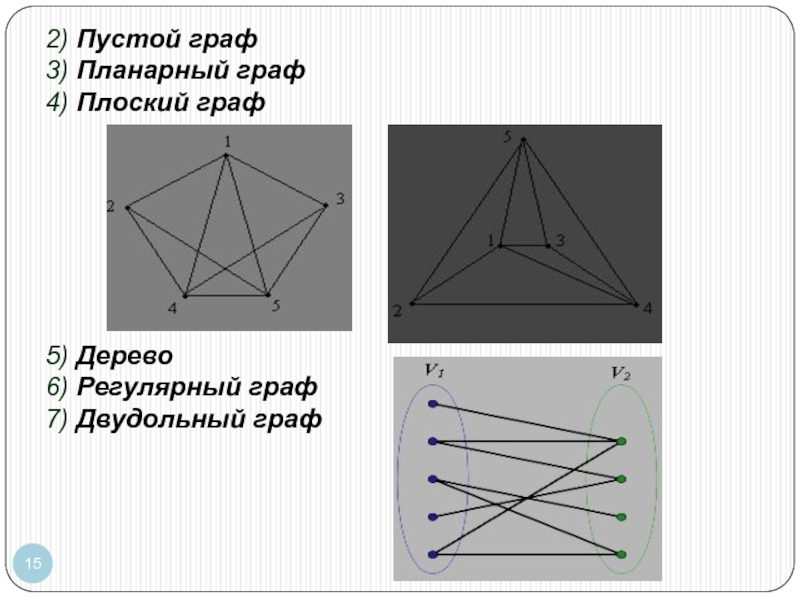
- 15. 2) Пустой граф 3) Планарный граф 4)
- 16. 1. Геометрическое представление Г.п. показывает
- 17. 4. Список смежности вершин (рёбер). Таблица
- 18. Пусть G – связный взвешенный граф,
- 19. Эксцентриситет вершины v в графе G(V, E)
- 20. Обобщение понятий центра и медианы графа 1)
- 21. Задачи размещения Выбор “наилучшего” размещения объектов
- 22. Задача о кратчайшем пути (к.п.): нахождение
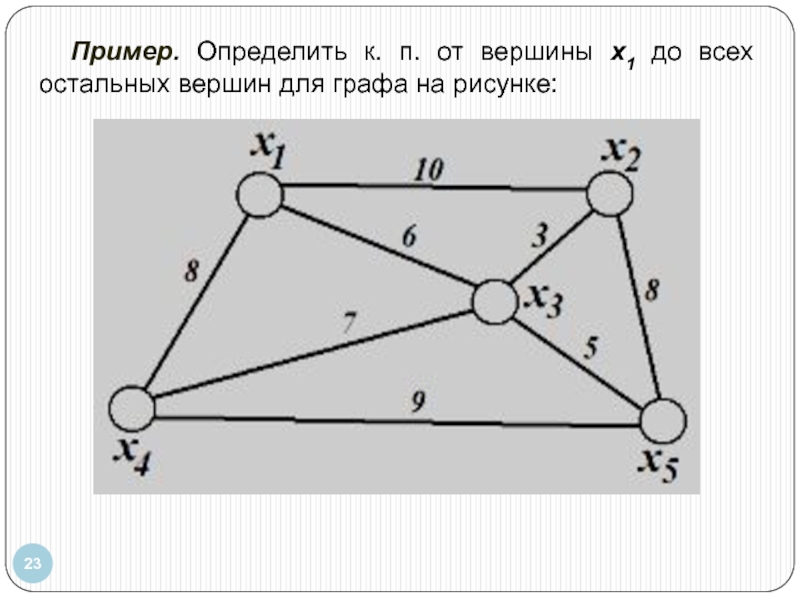
- 23. Пример. Определить к. п. от вершины x1
- 24. Наиболее универсальный алгоритм нахождения к. п.
- 25. Дерево конечный связный граф без циклов. Остовное
- 27. Алгоритм Краскала Шаг 1 Минимальный покрывающий
- 29. Алгоритм Прима Алгоритм наращивания минимального остова.
- 30. Эйлеров цикл и задача китайского почтальона
- 32. Задача китайского почтальона Задача нахождения эйлерова
- 33. Пусть в графе G, проходит некоторое количество
- 34. Условие 1. 0 < f(xi, xJ) <
- 35. Основная задача: определить максимальный поток, протекающий
- 36. Понятие разреза Величина разреза суммарный
- 37. Методы определения минимального разреза: 1. Метод двойственного
- 38. Граф G* называется двойственным для графа
- 39. Метод насыщенных рёбер Не
- 40. 3. Из вершины i помечаются смежные непомеченные
- 41. 2) Процедура изменения потока. Если сток t
Слайд 1МАТЕМАТИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ
СЕТЕЙ СВЯЗИ
Ирина Геннадьевна Квиткова
ст. преп. кафедры ПДС и
Слайд 2Основные понятия моделирования
Моделирование
замещение исследуемого объекта-оригинала его условным образом, описанием или другим
Модель
физический или абстрактный объект, свойства которого сходны со свойствами исследуемого объекта.
Требования к модели:
Адекватность;
Полнота;
Гибкость;
Трудоёмкость разработки.
Слайд 3Основные этапы моделирования:
1) Разработка модели;
2) Исследование модели и получение выводов.
При построении моделей объектов используется системный подход:
объект как СИСТЕМА,
действующая в некоторой среде
СИСТЕМА –
группа взаимосвязанных элементов, действующих совместно с целью выполнения заранее поставленной задачи.
ОБЪЕКТ как набор подсистем, элементов и связей
Слайд 4Стадии построения модели:
1. мысленная модель;
2. концептуальная модель;
3. формальная модель.
Представление мысленной
СМ делятся на:
описательные (любое описание объекта);
объяснительные (ответ на вопрос: почему это происходит?);
прогностические (описывает будущее поведение объекта).
Слайд 5 Концептуальная модель (КМ)
СМ, при формулировании которой используются понятия и представления
Виды КМ:
логико-семантическая (описание в предметной области);
структурно-функциональная
(изучение элементов системы и связей между ними);
причинно-следственные
(объяснение и прогнозирование поведения).
Формальная модель представлена с помощью формальных языков: математический аппарат, алгоритмические языки, языки моделирования.
Слайд 6Методы моделирования
Математическое моделирование
исследование явлений с помощью их
математических моделей (ММ).
отношения между
(замена)
отношения между математическими объектами
Физическое моделирование (макетирование)
исследование явлений на физических моделях
изучаемый процесс воспроизводят
с сохранением его физической природы
(реальное воплощение интересующих
физических свойств оригинала)
Слайд 7Этапы математического моделирования
1) - постановка задачи;
- определение объекта и
- задание критериев (признаков) изучения объекта.
Математическая формулировка задачи –
в виде геометрических образов, функций, систем уравнений.
Описание объекта (явления) –
непрерывная (дискретная), детерминированная (случайная) формы.
Цель мат. моделирования
анализ реальных процессов (в природе или технике) математическими методами.
2) Выбор типа ММ (определяет направление исследования).
Слайд 8 Виды ММ :
аналитическая
для простых систем,
отражает связь
процессы системы записываются в виде алгебраических, дифференциальных, интегральных уравнений;
- имитационная (компьютерная программа)
для сложных систем;
воспроизводит процесс функционир-ия системы во t-и.
3) Анализ полученных результатов.
Слайд 9Построение моделей сети связи
Решение задач, связанных с проектированием реальных сетей;
Анализ и
Морфологическое описание сетей электросвязи
1. Элементы сетей:
- пункты связи: сетевой узел, сетевая стация, узел связи, оконечная станция (пункт), узел коммутации;
- линии сетей связи: линия передачи, соединительная линия, канал электросвязи, канал вторичной сети.
2. Структуры сетей:
- первичной сети;
- вторичной сети;
- электросвязи.
Слайд 103. Технология обслуживания:
- метод коммутации;
- кроссировка каналов;
- передача информации
4. Внешние воздействия:
- поток заявок;
- поток освобождений (окончание передачи);
- поток отказов элементов сети;
- поток восстановлений элементов.
5. Критерии эффективности:
- экономические;
- качества и надежности передачи;
- живучести (сохранение работоспособности при разрушении элементов сети).
6. Требования и ограничения (условия эксплуатации).
Слайд 11
ММ сетей связи:
1. Первичные сети.
Структура может быть задана графом G=(X,V),
где X=(x1,..., xn) – множество вершин (сетевые узлы),
V=(v1,…, vm) - множество ветвей (соединит. линии).
2. Вторичные сети (без реализации на первичной сети).
Может быть задана графом L=(Y,R),
где Y = (y1 ,…,yP) – множество вершин (узлы связи),
R=(r1,…,rT) – множество рёбер (каналы связи).
3. Сеть электросвязи
Структура задана гиперсетью.
Если нужно учитывать привязку первичной сети к местности или к линии связи каналов передачи, то она моделир-ся гиперсетью.
Слайд 12
Классификация задач проектирования сетей связи (СС)
1.Проектирование СС (ПСС).
2. Планирование развития
3. Построение ВС на базе ПС.
4. Оптимальное размещение пунктов связи.
5. Оптимальное распределение каналов ВС в ПС.
6. Реализация линий передачи по кратчайшим маршрутам.
7. Анализ СС:
- метрических характеристик;
- пропускной способности сети;
- показателей живучести;
- экономических показателей;
- показателей качества и надёжности.
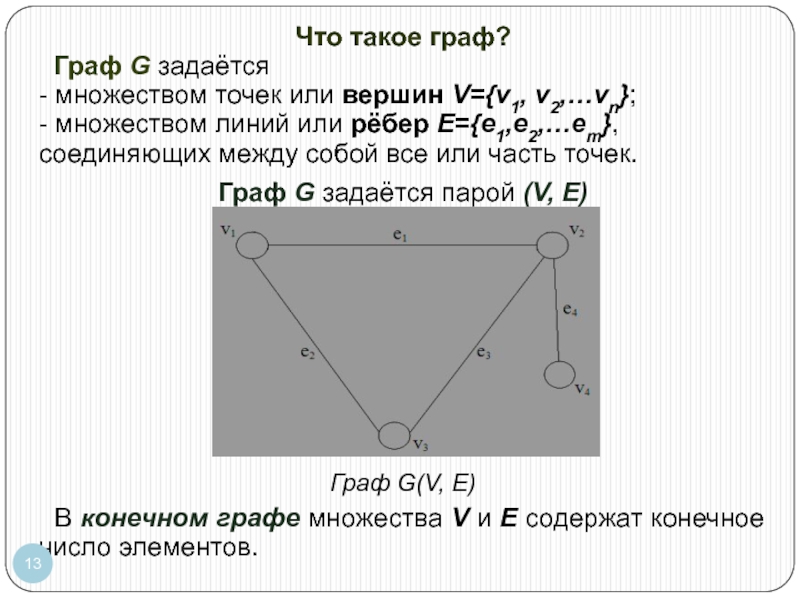
Слайд 13Что такое граф?
Граф G задаётся
- множеством точек или вершин V={v1,
- множеством линий или рёбер E={e1,e2,…em},
соединяющих между собой все или часть точек.
Граф G задаётся парой (V, E)
Граф G(V, E)
В конечном графе множества V и Е содержат конечное число элементов.
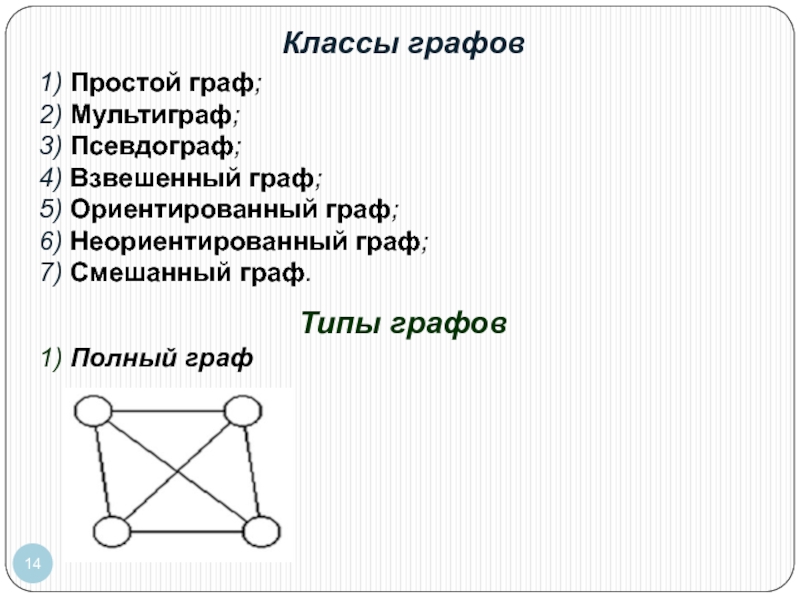
Слайд 141) Простой граф;
2) Мультиграф;
3) Псевдограф;
4) Взвешенный граф;
5) Ориентированный граф;
6) Неориентированный граф;
7)
Типы графов
1) Полный граф
Классы графов
Слайд 161. Геометрическое представление
Г.п. показывает реальную структуру сети.
2. Теоретико-множественное представление
- перечисление множеств V, E,
- отображение инциденций f.
3. Матричное представление задаёт граф в виде матрицы.
А) Матрица смежности вершин
Б) Матрица смежности рёбер
В) Взвешенная матрица смежности:
Для представления графов сетей.
Г) Матрица инциденции
Д) Матрица расстояний
Представление графов
Слайд 174. Список смежности вершин (рёбер).
Таблица с n=|V | строками и
первый столбец второй столбец
вершины (рёбра) графа вершины (рёбра), смежные с
5. KAO-FO представление.
2 массива: KAO и FO.
KAO:
FO:
Слайд 18Пусть G – связный взвешенный граф,
Расстояние между вершинами u и v
число, выражающее длину кратчайшего пути между вершинами u и v, в графе G; обозначается d(u, v).
1-й путь из u в v: u x1 x3 v,
длина l1 = 3+5+2 = 10;
2-й путь из u в v: u x1 x2 x3 v,
длина l2 = 3+4+2+2 = 11.
Расстояние u и v: d(u, v)= 10.
Метрические характеристики графа
Слайд 19Эксцентриситет вершины v в графе G(V, E)
e(v) = max{d(v, j)}, j∈V.
Радиус
Rad(G) = min{e(v)}, v∈V.
Диаметр графа
Diam(G) = max{e(v)}, v∈V.
Центр графа
вершина, у которой e(v) = Rad(G).
Периферийная вершина
вершина, у которой т.е. e(v) = Diam(G).
Передаточное число вершины графа G -
σ(v) = ∑ w(j)∙d(v, j), j∈V,
где w(j) – вес вершины j; d(v, j) – расстояние между v и j .
Медиана графа G вершина v* с
σ(v*) = min{σ(v)}, v∈V.
Слайд 20Обобщение понятий центра и медианы графа
1) b-центр
Пусть Vb – подмножество из
Тогда d(Vb, vJ) – наикратчайшее из расстояний между вершинами множества Vb и вершиной vJ, т.е.
d(Vb, vJ) = min[d(vi, vJ)], vi∈ Vb.
Эксцентриситет множества Vb:
e(Vb) = max[d(Vb, vJ)], vJ ∈ V.
b-кратный центр - множество Vb*, для которого
e(Vb*) = min[e(Vb)], Vb ϵ V.
2) b-медиана
Передаточное число множества вершин V
σ(Vb) = ∑ w(vJ)∙d(Vb, vJ), vJ ∈ V.
b-медиана - множество V̅b, для которого
σ(V̅b) = min{σ(Vb)}, Vb ϵ V.
Слайд 21Задачи размещения
Выбор “наилучшего” размещения объектов
(оборудования, аварийных служб, телефонных станций
1. Минимаксные задачи размещения
- Критерий оптимальности:
d(ПО, vJ) → min,
где ПО – пункт обслуживания,
vJ – самая отдалённая вершина графа,
d(ПО, vJ) – расстояние.
- Места размещения ПО: центры графа.
2. Минисуммные задачи размещения
- Критерий оптимальности:
∑ d(ПО, vJ) → min, vJ ∈ V,
где ∑ d(ПО, vJ) – сумма расстояний от ПО до всех вершин.
- Места размещения ПО: медианы графа.
Слайд 22Задача о кратчайшем пути (к.п.):
нахождение пути минимальной длины.
Невзвешенный граф:
длина пути
Взвешенный граф:
длина пути = сумма длин рёбер, составляющих путь.
Обобщения задачи о к.п.:
а) задача нахождения к. п. между вершиной v0 и всеми другими вершинами графа;
б) задача нахождения к. п. между всеми парами вершин (алгоритм Флойда).
Задача а) решается с помощью алгоритма Дейкстры, суть которого – поиск дерева к.п. (д.к.п.)
Алгоритмы нахождения кратчайших путей
Слайд 24
Наиболее универсальный алгоритм нахождения к. п.
Алгоритм Флойда
для решения задачи нахождения
Задача оптимальной трассировки кабельных л. с.:
- определение сети кабельной канализации;
- трассировка кабельных линий.
Для нахождения оптимального решения используются алгоритмы поиска к.п. в графе или д. к. п. от одного из узлов сети до всех остальных.
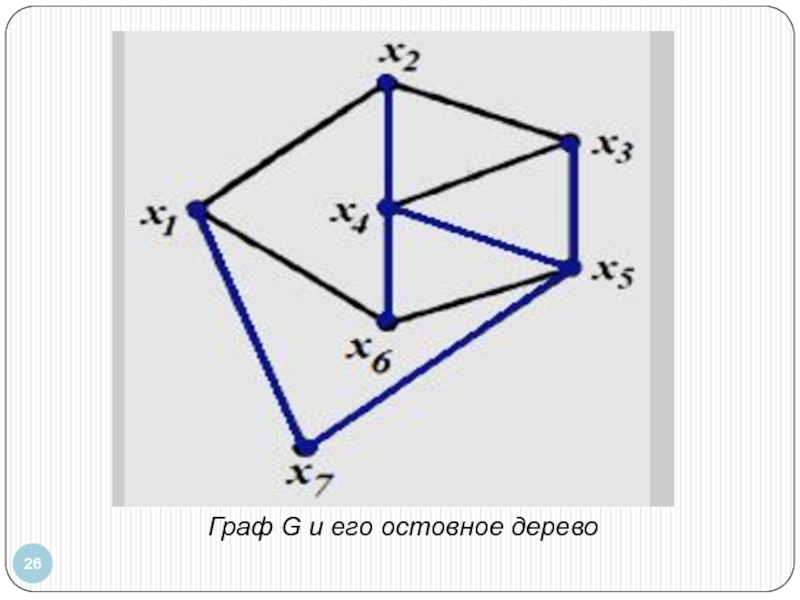
Слайд 25Дерево
конечный связный граф без циклов.
Остовное дерево (каркас, остов) графа G (X,
его ациклический связный суграф, в который входят все вершины.
Минимальное остовное дерево (МОД)
остовное дерево, суммарный вес рёбер которого минимален.
Практические задачи нахождения МОД:
1) объединить n районов города единой ТЛФ сетью так, чтобы суммарная стоимость соединений (кабеля) была минимальной;
2) Определения наиболее надёжной сети для передачи информации: веса рёбер – оценки потерь информации.
Алгоритмы построения
минимального остовного дерева
Слайд 27Алгоритм Краскала
Шаг 1
Минимальный покрывающий лес (м.п.л.) Т пуст.
Шаг 2
Упорядочить рёбра
Шаг 3
Начав с первого ребра в списке, добавлять безопасные рёбра в лес Т.
Безопасное ребро – ребро графа G, добавление которого не приводит к появлению цикла в Т.
Шаг 4
Повторять шаг 3 до тех пор, пока в Т не будет n-1 рёбер. Получившееся дерево Т - МОД для графа G.
Слайд 29 Алгоритм Прима
Алгоритм наращивания минимального остова.
Шаг 1
- М.п.л. Т состоит из
- Выбрать ребро, инцидентное корню, с минимальным весом среди всех инцидентных рёбер. Включить его в Т вместе с концевой вершиной.
Шаг 2
Рассмотреть рёбра, инцидентные включенным в Т вершинам. Выбрать ребро с мин. весом и включить его в Т вместе с концевой вершиной, ещё не включенной в дерево.
Шаг 3
Повторять шаг 2 до тех пор, пока в Т не будут включены все вершины.
Слайд 30Эйлеров цикл и
задача китайского почтальона
Эйлеров цикл
цикл в графе, который проходит
Эйлеров граф содержит эйлеров цикл (цепь).
В эйлеровом графе все вершины чётные/только 2 нечётные.
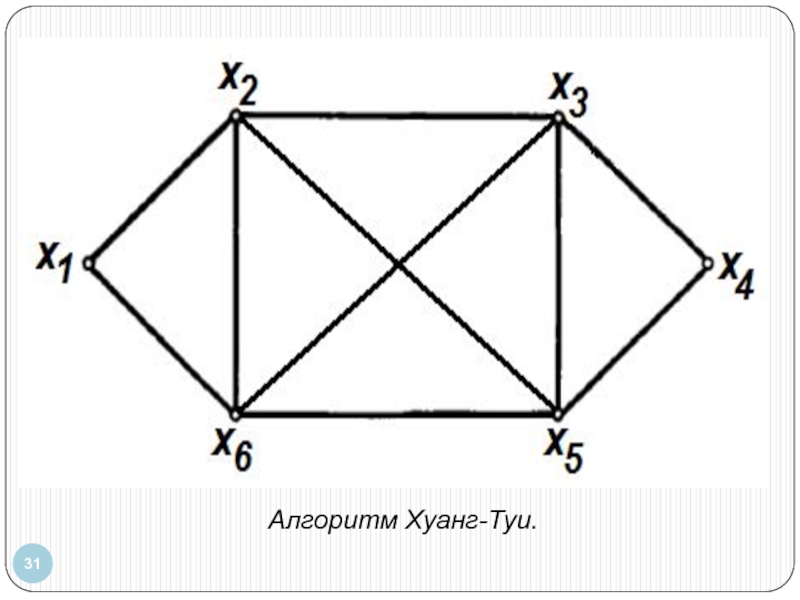
Алгоритмы нахождения эйлерова цикла (э.ц.)
1) алгоритм Флёри; 2) алгоритм Хуанг-Туи.
Слайд 32Задача китайского почтальона
Задача нахождения эйлерова цикла в графе является задачей обхода.
Для неэйлерова взвешенного («+» веса рёбер) графа задача обхода становится
задачей китайского почтальона
В графе требуется найти цикл, проходящий через каждое ребро графа по крайней мере 1 раз, и такой, что для него общий вес минимален.
Задача решается с помощью
алгоритма для задачи китайского почтальона.
Прикладная задача обхода:
Поиск неисправностей линейных сооружений сети с возвращением в исходный пункт.
Слайд 33Пусть в графе G, проходит некоторое количество единиц продукта от вершины
s – источник, t – сток.
Поток по дуге
число единиц продукта, проходящего по дуге e = (xi, xJ).
f(xi, xJ) - поток.
Сеть
связный граф G (X, E), веса рёбер которого являются их пропускными способностями (п.с.).
Поток из s в t в сети G(X, E)
это набор величин f(xi, xJ), удовлетворяющий четырем условиям:
Поток в сети
Слайд 34Условие 1.
0 < f(xi, xJ) < c(xi, xJ), (xi, xJ)∈E,
где c(xi,
Условие 2.
∑ fx+(e) - ∑ fx-(e)=0,
e∈Ix+ e∈Ixˉ
где Ix+- множество рёбер, по которым поток входит в x,
Ixˉ- множество рёбер, по которым поток исходит из х.
Условие 3.
∑ ft+(e) = C,
e∈It+
Условие 4.
∑fs- (e)=C,
e∈Isˉ
где С – величина суммарного потока.
Слайд 35Основная задача:
определить максимальный поток, протекающий от s к t.
Прикладная задача:
Анализ п. с. сети.
Теорема Форда-Фалкерсона
Величина максимального потока (м.п.) из s в t равна величине минимального разреза, отделяющего s от t.
(s, t) – (рёберный) разрез в графе G
некоторый набор рёбер, при удалении которых s и t оказываются в разных компонентах связности.
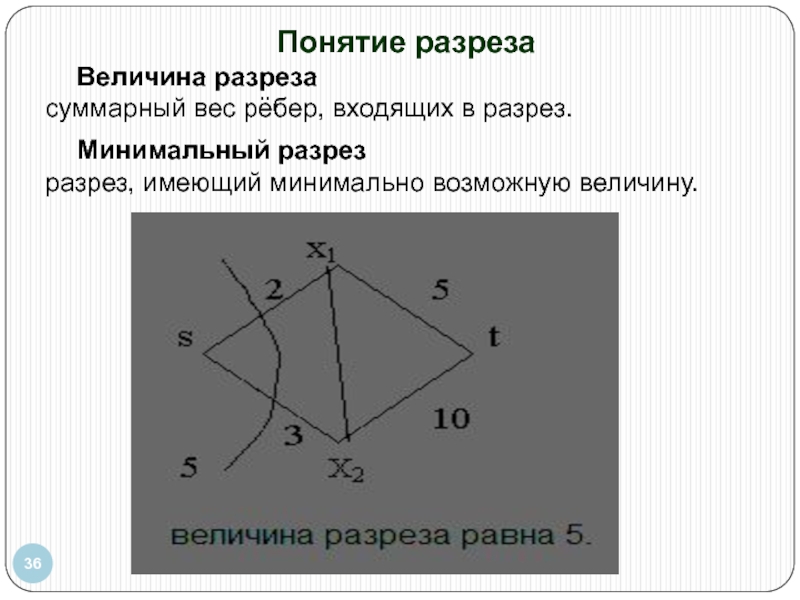
Слайд 36Понятие разреза
Величина разреза
суммарный вес рёбер, входящих в разрез.
Минимальный
разрез, имеющий минимально возможную величину.
Слайд 37Методы определения минимального разреза:
1. Метод двойственного графа;
2. Метод насыщенных рёбер.
Метод двойственного
Условия применения:
1. Граф G – плоский.
2. Вершины s и t находятся на внешней грани графа G.
3. Метод даёт численную величину м.п., не указывает рёбра, по которым он пройдёт.
Описание алгоритма
- Построить граф G*, двойственный исходному графу G.
- От вершины a графа G* до вершины b найти кратчайший путь (это минимальный разрез графа G).
- Определить численную величину минимального разреза (это величина м. п).
Слайд 38
Граф G* называется двойственным для графа G,
если выполняются два условия:
1)
вершина x* графа G*;
2) каждому ребру e графа G,
инцидентному грани h,
соответствует одно ребро e* графа G*,
инцидентное вершинам графа G*.
Двойственный граф плоского графа G также плоский.
Слайд 39Метод насыщенных рёбер
Не имеет ограничений в применении.
Описание алгоритма Форда-Фалкерсона
Пусть
Процедуры алгоритма:
1) помечивание вершин;
2) изменение потока.
1) Процедура помечивания вершин.
1. Исток s помечается меткой (+s, ∞).
2. Пометить вершины, смежные с s,
либо смежные с уже помеченной вершиной i (±x, e),
где х – вершина, из которой пришли в i,
е – поток по дуге (x, i).
Слайд 403. Из вершины i помечаются смежные непомеченные
вершины по правилу:
-
вершине j присваивается метка [+i, min(e, ciJ - fiJ)];
- если дуга направлена из j в i и поток по ней fJi > 0, то
вершине j присваивается метка [-i, min(e, fJi)].
Процесс помечивания заканчивается, если:
1) Ни одну вершину нельзя пометить, и сток не помечен.
найденный поток – максимальный,
алгоритм останавливается
2) Помечается сток.
Тогда производится изменение потока.
Слайд 412) Процедура изменения потока.
Если сток t получил метку (+k, d), то
потоки
- d + fiJ по дуге (i, j), если находимся в j (+i, m),
и переходим в i;
- d - fiJ по дуге (i, j), если находимся в j (-i, m),
и переходим в i.
Изменение потока начинается от t и продолжается до s.
Потом все метки стираются,
снова выполняется помечивание вершин.
Процесс продолжается, пока не найден м. п.
Область разреза между помеч. и непомеч. вершинами имеет величину м. п.
В миним. разрез входят рёбра, соединяющие помеч. вершины с непомеч-ми.