ВОЕННАЯ АКАДЕМИЯ СВЯЗИ
22 кафедра (сетей связи и систем коммутации)
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математические модели потоков телефонных вызовов презентация
Содержание
- 1. Математические модели потоков телефонных вызовов
- 2. Цели и вопросы занятия Изучить свойства
- 3. 1.
- 4. Характеристики потоков вызовов Параметр потока
- 6. 1. 5 Вариант
- 7. 1. 5 1. Простейший поток. Свойства и характеристики
- 8. 1. 6
- 9. 1. 7 При
- 10. 1. 8
- 12. 1. 10
- 13. 1. 11 2. Примитивный поток. Свойства и характеристики.
- 14. 1. 12
- 15. 1. 13 И, наконец,
- 16. 1. 14 3. Поток с повторными вызовами
- 17. 1. 15
- 18. 1. 16 4. Потоки Пальма и Эрланга
- 19. 1. 16
- 20. 1. 16
Слайд 1
Дисциплина
СЕТИ СВЯЗИ И СИСТЕМЫ КОММУТАЦИИ
Раздел 1. ТЕОРИЯ РАСПРЕДЕЛЕНИЯ ИНФОРМАЦИИ
Тема
Слайд 2Цели и вопросы занятия
Изучить свойства и характеристики основных математических моделей
Учебные вопросы:
Простейший поток. Свойства и характеристики.
Примитивный поток. Свойства и характеристики.
Поток с повторными вызовами.
Потоки Пальма и Эрланга.
Слайд 31.
1.Зотов В. М. Основы теории распределения информации.
2. Теория телетрафика / Корнышев Ю.Н., Пшеничников А.П., Харкевич А.Д. Учебник для вузов. – М.: Радио и связь, 1996 г.
Слайд 4
Характеристики потоков вызовов
Параметр потока - предел отношения вероятности поступления хотя
одного вызова за время [t, t + τ) к длине этого отрезка времени τ при τ → 0
Для нестационарных потоков:
Слайд 6
1.
5
Вариант 1
1. Дайте понятие ординарности.
2. Вызовы поступают на 3,
Вариант 2
1. Дайте понятие стационарности.
2. Какими из трех известных свойств может обладать (не обладать) поток вызовов от 10 абонентов. Ответ обосновать.
Вариант 3
1. Дайте понятие последействия.
2. Чему равна интенсивность стационарного потока вызовов, если известно, что за 4 часа поступило 64 вызова?
Слайд 8
1.
6
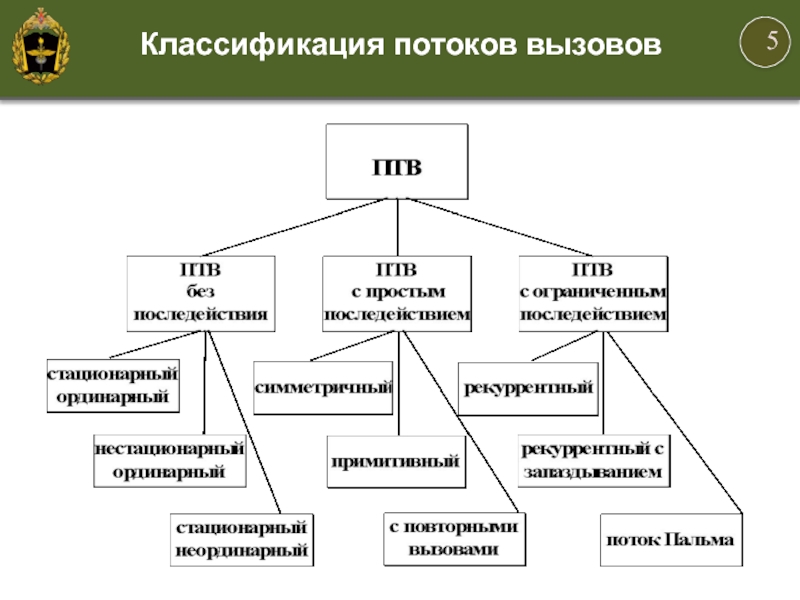
Простейшим потоком вызовов ППВ называется стационарный ординарный поток без последействия.
Поток
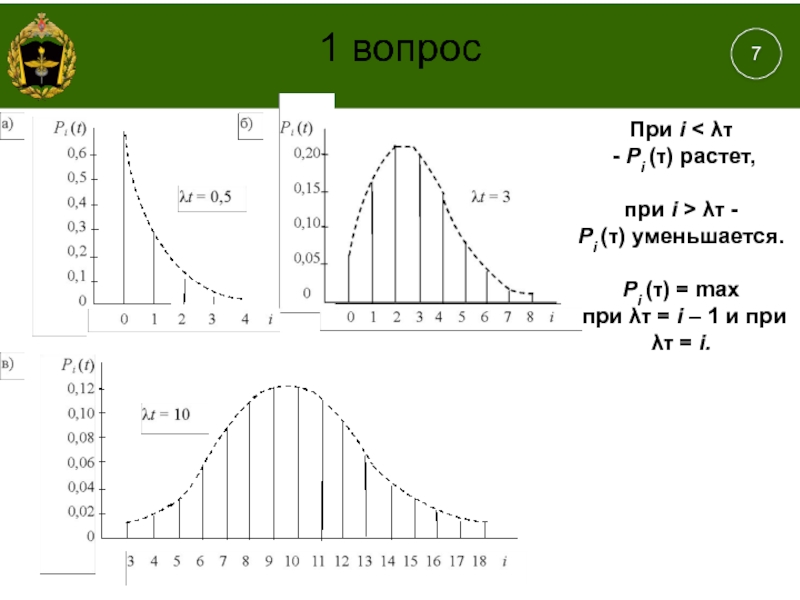
1 вопрос
При i < λτ - Pi (τ) растет, при i > λτ - Pi (τ) уменьшается.
Pi (τ) = max при λτ = i – 1 и при λτ = i.
Слайд 11
Это равносильно
1.
9
Другой способ задания случайного потока - определение закона распределения вероятностей промежутков времени между вызовами.
Функция распределения F (z) - вероятность того, что промежуток времени между вызовами будет меньше заданного z
Используя формулу Пуассона , при i=0
получим:
Слайд 12
1.
10
.
математическое ожидание и дисперсия числа
При объединении независимых простейших потоков с параметрами образуется общий простейший поток с параметром
При разъединении поступающего простейшего потока с параметром на n направлений, поток i-го направления также будет простейшим.
Слайд 14
1.
12
Примитивным называется поток с простым последействием, параметр которого зависит только
– параметр потока вызовов от одного свободного источника.
Среднее значение параметра:
Среднее значение параметра от одного источника:
Слайд 19
1.
16
4 вопрос
Поток с одинаково распределенными промежутками времени между
вызовами
Поток с и
называется рекуррентным с запаздыванием.
Ординарный стационарный рекуррентный поток с запаздыванием называется потоком Пальма.
Важными для практики образцами потоков Пальма являются потоки Эрланга, которые образуются в результате «просеивания» простейших потоков.