- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логики умолчаний презентация
Содержание
- 1. Логики умолчаний
- 2. Введение Всякая интеллектуальная деятельность опирается на знания.
- 3. Введение Сегодня мы очень часто работаем с
- 4. Раймонд Рейтер 12.06.1939-16.09.2002 Канадский ученый и логик.
- 5. Определение языка Логика умолчания (default logic) —
- 6. Определение языка Логики Рейтера отличаются от модальных
- 7. Определение языка К примеру, правило, которым руководствуются
- 8. Определение языка Почему же классическая логика непригодна
- 9. Определение языка Эта ситуация может быть представлена
- 10. Определение языка Умолчания могут быть использованы для
- 11. Определение языка Подобные умолчания встречаются во многих
- 12. Определение языка
- 13. Синтаксис
- 14. Синтаксис
- 15. Синтаксис
- 16. Синтаксис Множество формул является расширением для
- 17. Примеры
- 18. Примеры
- 19. Примеры
- 20. Система GADEL Теперь кратко напомним понятия, используемые
- 21. Система GADEL Генетический алгоритм включает: - представление
- 22. Система GADEL Приведем общий механизм. Хромосомы (Gi)
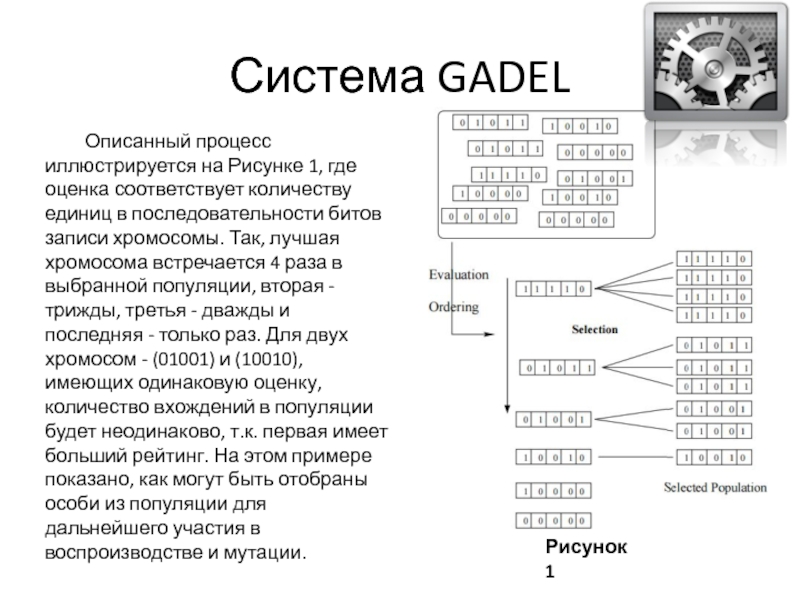
- 23. Описанный процесс иллюстрируется на Рисунке 1, где
- 24. Система GADEL Теперь генетические операторы могут производить
- 25. Оператор мутации работает следующим образом: - для
- 26. Формальное описание системы
- 27. Таким образом, обеспечить эффективность и сходимость
- 28. Представление
- 29. Представление
- 30. Пример
- 31. Оценивание
- 32. Комментарии к таблице Объяснение таблицы - Случаи
- 33. Технические улучшения
- 34. Результаты экспериментов: система GADEL Вся система
- 35. В целом, системы DeReS и GADEL используют
- 36. В первой колонке таблицы приводятся используемые теории
- 37. По результатам, опубликованным в таблице, можно сказать,
- 38. Общий метод, описанный выше, воздвигает новые основы
- 39. Другие системы DeReS (Default Reasoning System) –
- 40. Выводы Логики умолчаний находят широкое применение в
- 41. Литература Достоверный и правдоподобный вывод в интеллектуальных
Слайд 1Логики умолчаний
Выполнили: Плотников Денис, Нургалиев Радес, гр. 09-208, ИВМиИТ
Преподаватель: Михайлов Валерий
Слайд 2Введение
Всякая интеллектуальная деятельность опирается на знания. В эти знания включаются характеристики
Принципиальное отличие систем искусственного интеллекта состоит в том, что для такого рода систем разработчик не готовит конкретные программы для исполнения. Он лишь даёт машине нужное задание, а программу, выполняющую это задание, система должна построить сама. Для этого нужны знания как о предметной области, к которой относится задание, так и о том, как строятся программы. Все эти знания хранятся в интеллектуальных системах в специальном блоке, называемой базой знаний.
Слайд 3Введение
Сегодня мы очень часто работаем с теми или иными базами знаний.
Описание поведения таких систем, т.е. пользовательский сценарий (англ. Use Case), может быть произведено на языке логики умолчаний.
В данной работе предложен разбор механизма реагирования системы на внешние запросы c последующим анализом на примере конкретной системы GADEL(Genetic Algorithms for DEfault Logic), опирающейся, как понятно из названия, на генетические алгоритмы поиска.
Слайд 4Раймонд Рейтер
12.06.1939-16.09.2002
Канадский ученый и логик. Один из основоположников немонотонных логик. Работал
Слайд 5Определение языка
Логика умолчания (default logic) — это формальная система, в которой
Утверждение:
«А есть обычно (как правило, типично) В»
интерпретируется как:
«Если х есть А и непротиворечиво предположить, что х есть В, тогда х есть В»
Слайд 6Определение языка
Логики Рейтера отличаются от модальных подходов одним важным аспектом: вместо
При неполной информации мы вынуждены получать всего лишь правдоподобные предположительные заключения. Часто имеются утверждения, которые в большинстве случаев истинны, но допускают исключения. Логика первого порядка не является подходящей для выражения исключений, так как она требует явного упоминания всех исключений, что на практике невозможно выполнить .
Слайд 7Определение языка
К примеру, правило, которым руководствуются организаторы футбольных матчей в зимнее
Это умолчание можно интерпретировать следующим образом: если нет информации о том, что газон стадиона будет заснежен, разумно положить
и прийти к заключению, что матч проведен будет (начнется подготовка стадиона к матчу). Но если в ночь перед матчем пройдет обильный снегопад, то такое предположение просто не может быть сделано. Теперь мы владеем информацией о том, что будет снег и не можем положить
, а умолчание не может быть применено. В этом случае, мы должны воздержаться от заключения .
Слайд 8Определение языка
Почему же классическая логика непригодна для моделирования этой ситуации? Пусть
Проблема здесь в том, что мы должны точно установить, что не будет никакого снега на стадионе прежде, чем применять это правило. Но это будет означать, что зимой не будет проведено ни одного из положенных по календарю матча. Здесь важно понимать разницу между необходимостью знать, что не снег идти не будет, и возможностью предположить, что снег все же пойдет. Умолчания поддерживают построение заключение на основе предположений.
Слайд 9Определение языка
Эта ситуация может быть представлена умолчанием:
вместе с классическим правилом
Если нам точно известно, что выпадет снег, выводим средствами классической логики, поэтому не можем принять , требуемое умолчанием. В таком представлении умолчание говорит «Обычно все футбольные матчи проводятся» , а исключения к этому правилу представлены средствами классической логики, как то, что представлено выше.
Слайд 10Определение языка
Умолчания могут быть использованы для моделирования прототипичных рассуждений, что означает,
Другая форма рассуждений по умолчанию – рассуждения без риска. Это относится к случаям, когда мы приходим к заключению, пусть и не самому вероятному, потому что все остальные(вероятно, неверные) заключения могут привести к плохим последствиям. Наверное, лучший пример – главный принцип правосудия в западных странах: «В отсутствии доказательств можно предположить, что обвиняемый невиновен»(«Не пойман – не вор»):
Слайд 11Определение языка
Подобные умолчания встречаются во многих прикладных областях. Приведем пример юридического
и классическим правилом .
Слайд 16Синтаксис
Множество формул является расширением для тогда и только тогда, когда
Расширение можно охарактеризовать так. Строим последовательность формул , полагая и и и
для . Множество есть расширение для тогда и только тогда когда .
Слайд 20Система GADEL
Теперь кратко напомним понятия, используемые в Генетических Алгоритмах, которыми будем
Генетические алгоритмы основаны на принципах естественного отбора, поэтому будем использовать понятия, присущие разделу "Генетика". Для начала рассмотрим популяцию, которая представлена своими хромосомами. Каждая хромосома представляет собой потенциальное решение данной задачи. Семантика хромосомы (так называемый фенотип) должна быть внешне определена пользователем. Затем генетические операторы определяют эволюцию популяции для получения все лучших особей.
Слайд 21Система GADEL
Генетический алгоритм включает:
- представление возможных решений. В большинстве случаев, хромосомы
- способ создания изначальной популяции
- функцию оценивания eval. Эта функция оценивает каждое потенциальное решение данной задачи.
- генетические операторы, необходимые для применения принципов наследственности и изменчивости к популяции. Будут рассмотрены два основных вида операторов. Кроссовер производит обмен генетическим материалом между особями(моделирует процесс скрещивания особей) . Мутация произвольно изменяет один или несколько генов выбранной хромосомы.
- параметры: размер популяции psize и вероятности генетических операторов: кроссовера - pc и мутации – pm.
Слайд 22Система GADEL
Приведем общий механизм. Хромосомы (Gi) - последовательности битов длины n.
Процесс отбора, представленный ниже, основан на упорядочении особей по их оценке.
- Для каждой хромосомы Gi, i ∈ {1.. psize }, подсчитывается оценка eval(Gi).
- Упорядочивание особей популяции по подсчитанным оценкам (в упорядоченном списке все особи - различны).
Затем строится промежуточная популяция путем выбора хромосом по следующим правилам:
- считывание упорядоченного списка различных хромосом.
- определение количества вхождений хромосом в популяцию(обратное упорядочивание). Каждая следующая в рейтинге хромосома должна войти в популяцию на один раз меньше предыдущей. К примеру, если лучшая хромосома войдет в популяцию N раз, следующая за ней войдет в популяцию (N - 1) раз и т.д.
- это распределение хромосом в популяции определяется пользователем.
Однако, общее кол-во хромосом в популяции должно быть равно изначально заданному значению psize.
Слайд 23Описанный процесс иллюстрируется на Рисунке 1, где оценка соответствует количеству единиц
Рисунок 1
Система GADEL
Слайд 24Система GADEL
Теперь генетические операторы могут производить действия с отобранными особями. Кроссовер
- выбирает две случайные хромосомы в сформированной популяции.
- генерирует случайное число r ∈ [0, 1].
- если r > pc, то действия кроссовера возможны:
1) выбирается случайная позиция гена хромосомы p ∈ {1, . . . , n − 1}
2) из выбранных хромосом (a1, ..., ap, ap+1, ..., an) и (b1, ..., bp, bp+1, ..., bn) получим (a1, ..., ap, bp+1, ..., bn) и (b1, ..., bp, ap+1, ..., an), как показано на Рисунке 2.
- если действия кроссовера невозможны, то выбранные хромосомы помещаются обратно в популяцию.
Рисунок 2
Слайд 25Оператор мутации работает следующим образом:
- для каждой хромосомы Gi, i ∈
- если r > pm, то бит bj инвертируется.
Этот процесс повторяется для генерации удачных популяций, а в конце процесса необходимо определить некоторое количество лучших популяций для дальнейшего исследования. Лучшая хромосома каждой популяции, полученная с помощью функции оценивания, есть лучшее решение данной задачи.
Очевидно, что основная трудность в определении Генетических Алгоритмов заключается в поиске ошибок в выборе представления популяций, а также в определении процесса оценивания. Огромный объем работы требует подбор параметров psize, pc и pm. Все эти шаги полностью разобраны в следующем разделе.
Система GADEL
Слайд 27
Таким образом, обеспечить эффективность и сходимость алгоритма представляется невозможным. Одним из
Подобных трудностей поможет избежать другой подход, состоящий в сосредоточении больше на умолчаниях, чем на следствиях умолчаний. Кроме того, этот подход более естественный, т.к. расширение полностью определяется набором умолчаний. Следующие определения определяют формальную основу, состоящую из схемы представления и процесса оценивания.
Формальное описание системы
Слайд 32Комментарии к таблице
Объяснение таблицы
- Случаи 2,3,4:
Следствие γi содержится в расширении-кандидате (G|2i-1
- Случаи 5,9,13:
Следствие умолчания не содержится в CE(G), в то время, как должно содержаться, т.к. предпосылка умолчания содержится в расширении и отрицания в обосновании умолчаний не выводимы из следствия.
- В остальных случаях:
Таблица 1
Слайд 34Результаты экспериментов: система GADEL
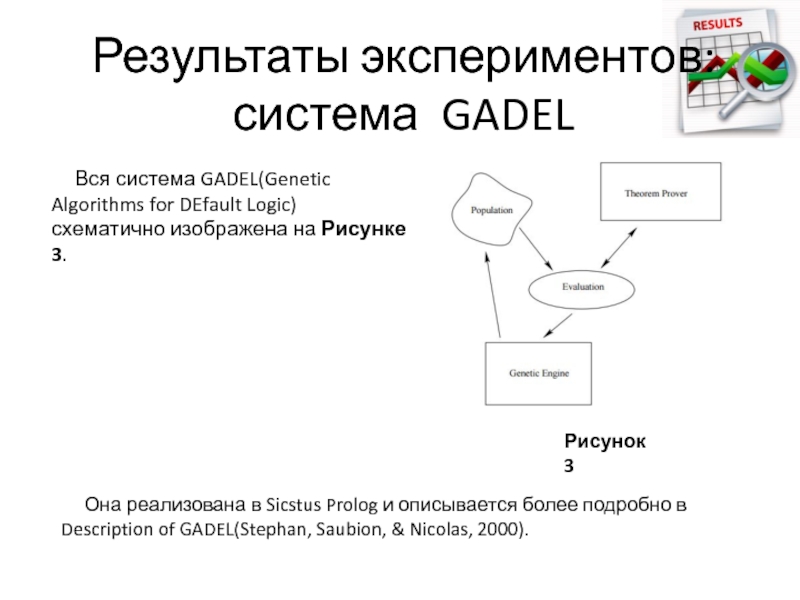
Вся система GADEL(Genetic Algorithms for DEfault Logic) схематично
Она реализована в Sicstus Prolog и описывается более подробно в Description of GADEL(Stephan, Saubion, & Nicolas, 2000).
Рисунок 3
Слайд 35В целом, системы DeReS и GADEL используют один и тот же
Результаты экспериментов: система GADEL
Но система DeReS исследует пространство поиска процедурой поиска с возвратом (backtracking procedure), тогда как действия в GADEL основываются на принципах Генетических Алгоритмов для быстрейшего поиска "хороших" кандидатов.
Слайд 36В первой колонке таблицы приводятся используемые теории по умолчанию. Для первых
Результаты экспериментов: система GADEL
Слайд 37По результатам, опубликованным в таблице, можно сказать, что система DeReS имела
Результаты экспериментов: система GADEL
Слайд 38Общий метод, описанный выше, воздвигает новые основы поиска расширений теории Логики
В настоящее время, главной задачей является интеграция свойства прочности в функцию оценивания, которое не должно сильно увеличить время вычислений. Эффективность может быть улучшена объединением других методов поиска, например, эвристических методов. Еще одной особенностью рассмотренного подхода является возможность его распараллеливания. В самом деле, оценка всей популяции и генетические манипуляции над ней могут быть распределены на нескольких процессорах без возникновения трудностей. Эти и многие другие улучшения алгоритма производятся по сей день.
Заключение
Слайд 39Другие системы
DeReS (Default Reasoning System) – автоматизированная система рассуждений по умолчаний,
Xray (Prolog Technology Theorem Prover for Default Reasoning) – автоматическая система доказательства теорем для рассуждений по умолчанию в логике умолчаний.
Слайд 40Выводы
Логики умолчаний находят широкое применение в интеллектуальных системах, в различных методах
Таким образом, логики умолчаний могут быть полезны во многих сферах профессиональной деятельности человека.
Слайд 41Литература
Достоверный и правдоподобный вывод в интеллектуальных системах (Вагин В.Н., Головина Е.Ю.,
Genetic Algorithms for Extension Search in Default Logic (Pascal Nicolas, Frederic Saubion, Igor Stephan)
Искусственный интеллект. Системы и модели http://www.rriai.org.ru/geneticheskie-algoritmyi.html)
Education Library (on-line библиотека электронных учебных пособий)