- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логические основы ЭВМ презентация
Содержание
- 1. Логические основы ЭВМ
- 2. www.themegallery.com Company Name Основные термины и понятия
- 3. Логические операции (основные) ОТРИЦАНИЕ
- 4. Логические операции (основные) КОНЪЮНКЦИЯ
- 5. Логические операции (основные) ДИЗЪЮНКЦИЯ
- 6. Логические операции ИМПЛИКАЦИЯ Используя операции
- 7. Логические операции ЭКВИВАЛЕНЦИЯ Используя
- 8. Пример записи высказываний "Быть иль не быть
- 9. Приоритет выполнения логических операций Приоритет (порядок выполнения)
- 10. Таблицы истинности Таблица истинности представляет собой таблицу,
- 11. Порядок составления таблицы истинности 1. Определить количество
- 12. Законы булевой алгебры (законы логики) 1.
- 13. Пример 1. В классе оказалось разбито
- 14. Примеры Записать формулу по заданной функциональной
- 15. Задания 1. Записать формулу
- 16. Задания Построить таблицу истинности и схему для логической функции
- 17. Катков К.А. Спасибо за внимание!
Слайд 2www.themegallery.com
Company Name
Основные термины и понятия
Логическое высказывание – это любое утверждение,
Логические переменные – переменные, которые принимают только два значения –"истина" или "ложь", обозначаемые, соответственно, "1" и "0".
Слайд 3Логические операции (основные)
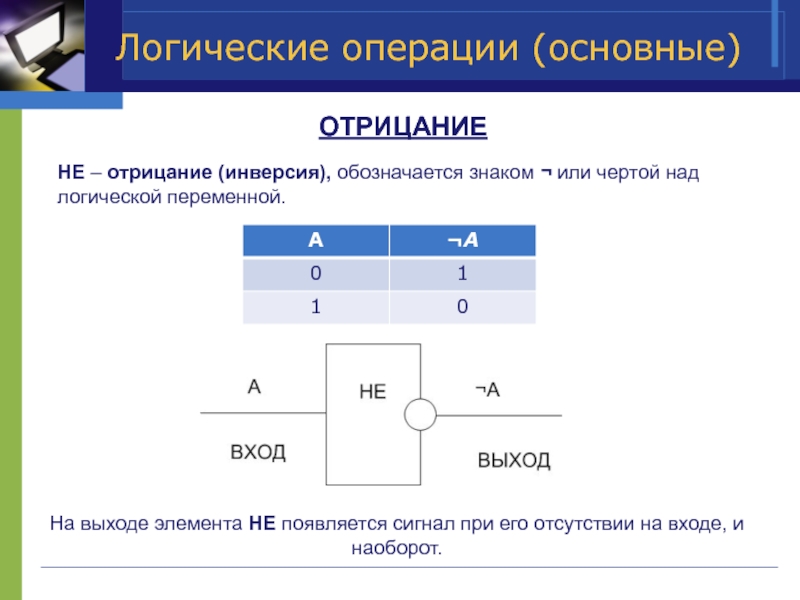
ОТРИЦАНИЕ
НЕ – отрицание (инверсия), обозначается знаком ¬ или
На выходе элемента НЕ появляется сигнал при его отсутствии на входе, и наоборот.
Слайд 4Логические операции (основные)
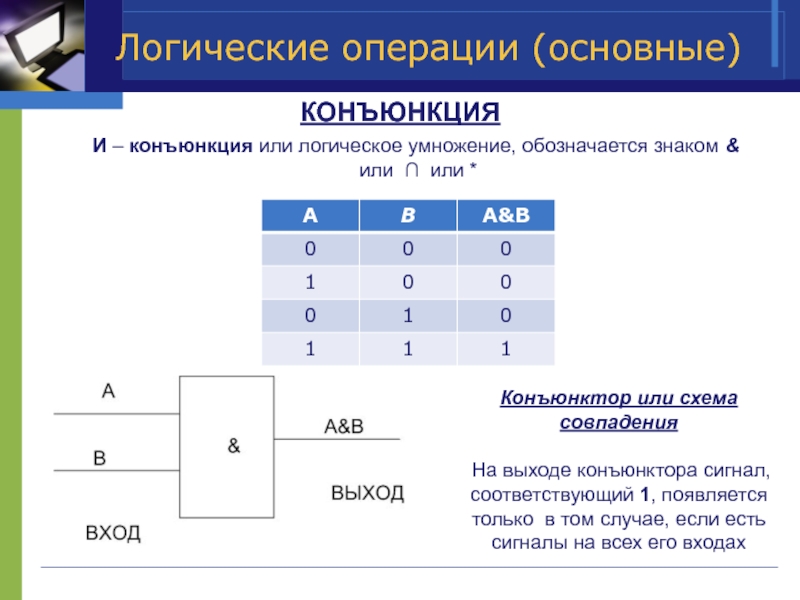
КОНЪЮНКЦИЯ
И – конъюнкция или логическое умножение, обозначается знаком
или ∩ или *
Конъюнктор или схема совпадения
На выходе конъюнктора сигнал, соответствующий 1, появляется только в том случае, если есть сигналы на всех его входах
Слайд 5Логические операции (основные)
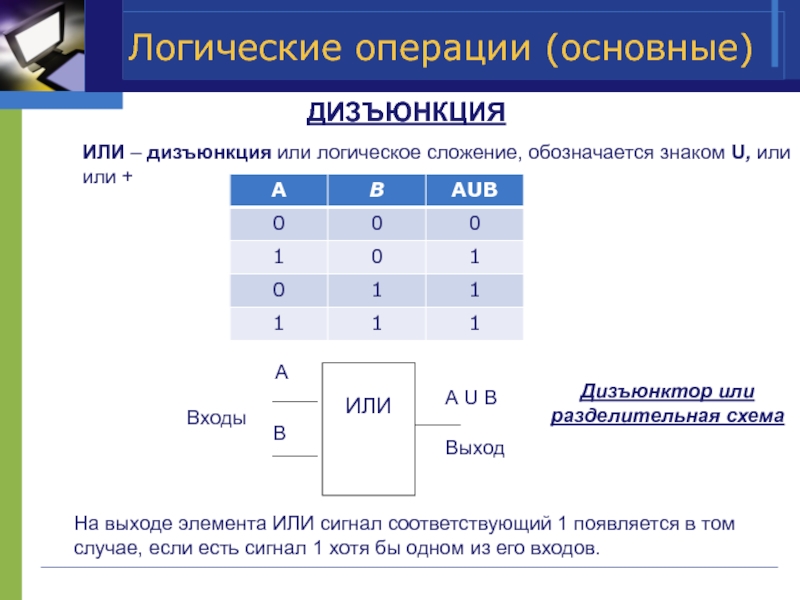
ДИЗЪЮНКЦИЯ
ИЛИ – дизъюнкция или логическое сложение, обозначается знаком
На выходе элемента ИЛИ сигнал соответствующий 1 появляется в том случае, если есть сигнал 1 хотя бы одном из его входов.
Дизъюнктор или разделительная схема
А
Слайд 6Логические операции
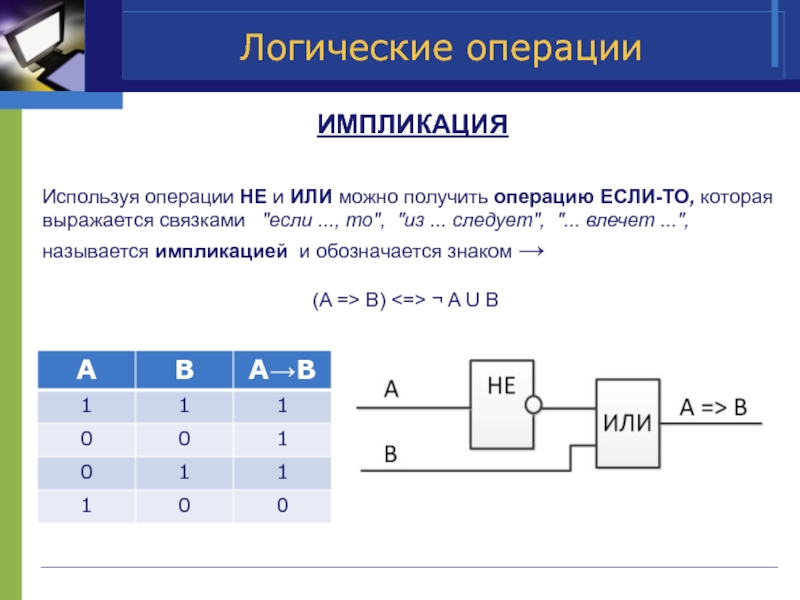
ИМПЛИКАЦИЯ
Используя операции НЕ и ИЛИ можно получить операцию ЕСЛИ-ТО, которая
(A => B) <=> ¬ A U B
Слайд 7Логические операции
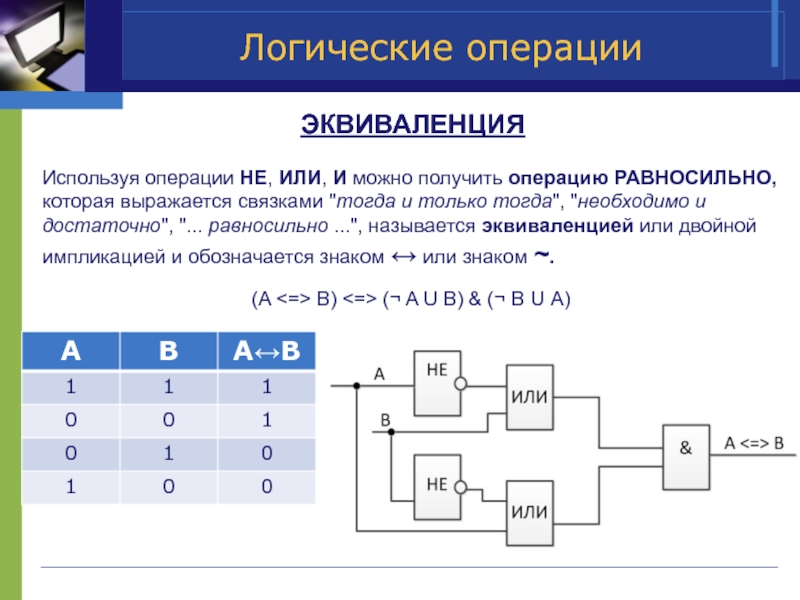
ЭКВИВАЛЕНЦИЯ
Используя операции НЕ, ИЛИ, И можно получить операцию РАВНОСИЛЬНО, которая
(A <=> B) <=> (¬ A U B) & (¬ B U A)
Слайд 8Пример записи высказываний
"Быть иль не быть - вот в чем вопрос.«
А U ¬ A <=> В
"Если хочешь быть красивым, поступи в гусары." (К. Прутков)
А => В
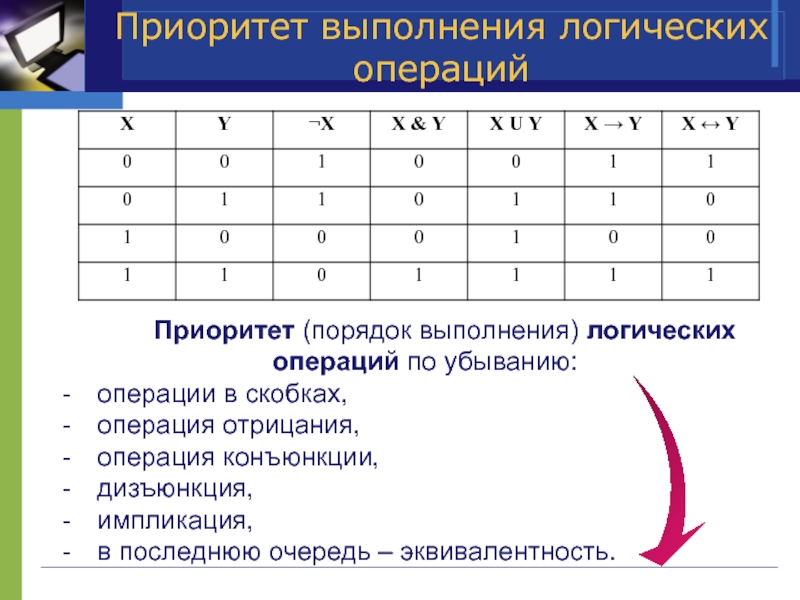
Слайд 9Приоритет выполнения логических операций
Приоритет (порядок выполнения) логических операций по убыванию:
операции в
операция отрицания,
операция конъюнкции,
дизъюнкция,
импликация,
в последнюю очередь – эквивалентность.
Слайд 10Таблицы истинности
Таблица истинности представляет собой таблицу, устанавливающую соответствие между всевозможными наборами
Функция, которая принимает:
значение "истина" для всех наборов значений переменных, называется тождественно истинной функцией или тавтологией;
значение "ложь" для всех наборов значений переменных, называется тождественно ложной функцией или противоречием;
для некоторых наборов значений переменных значение "истина", а для других – значение "ложь", называется выполнимой логической функцией.
Если две функции А и В при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.
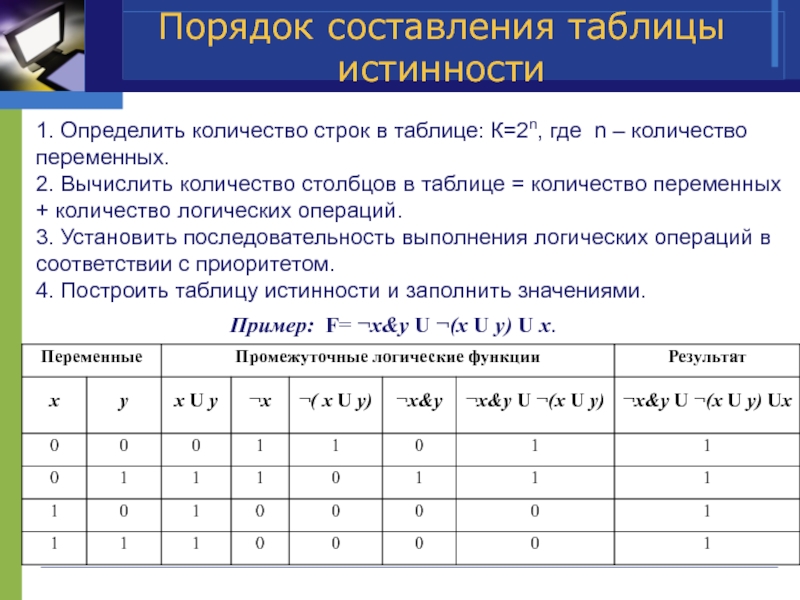
Слайд 11Порядок составления таблицы истинности
1. Определить количество строк в таблице: К=2n, где
2. Вычислить количество столбцов в таблице = количество переменных + количество логических операций.
3. Установить последовательность выполнения логических операций в соответствии с приоритетом.
4. Построить таблицу истинности и заполнить значениями.
Пример: F= ¬x&y U ¬(x U y) U x.
Слайд 12Законы булевой алгебры (законы логики)
1. ¬¬ А A
Слайд 13Пример
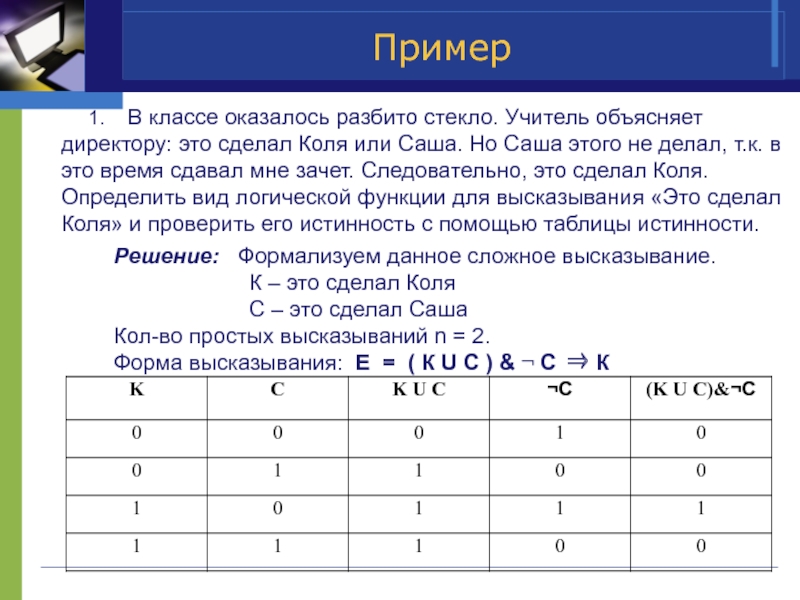
1. В классе оказалось разбито стекло. Учитель объясняет директору: это
Решение: Формализуем данное сложное высказывание.
К – это сделал Коля
С – это сделал Саша
Кол-во простых высказываний n = 2.
Форма высказывания: Е = ( К U C ) & ¬ С ⇒ К
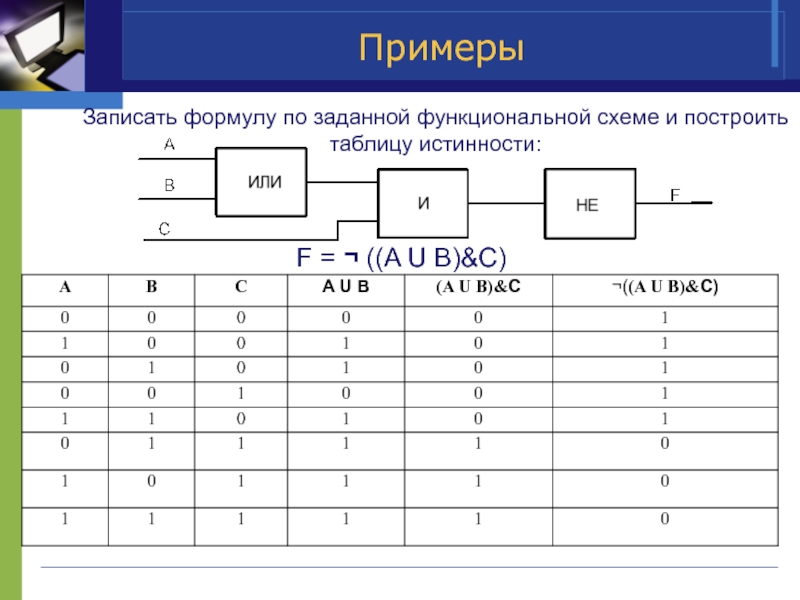
Слайд 14Примеры
Записать формулу по заданной функциональной схеме и построить таблицу истинности:
F =
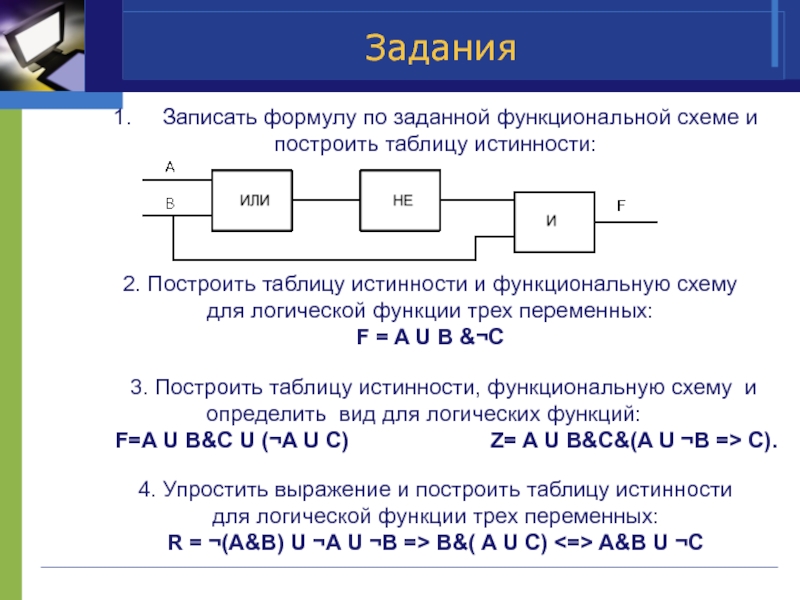
Слайд 15Задания
1. Записать формулу по заданной функциональной схеме и построить
2. Построить таблицу истинности и функциональную схему
для логической функции трех переменных:
F = A U B &¬C
3. Построить таблицу истинности, функциональную схему и определить вид для логических функций:
F=A U B&C U (¬A U C) Z= A U B&C&(A U ¬B => C).
4. Упростить выражение и построить таблицу истинности
для логической функции трех переменных:
R = ¬(A&B) U ¬A U ¬B => B&( A U C) <=> A&B U ¬C