- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логические операции презентация
Содержание
- 1. Логические операции
- 2. Таблица истинности – таблица, определяющая значение сложного высказывания при всех возможных значениях простых высказываний
- 3. Логическая операция КОНЪЮНКЦИЯ Название: логическое
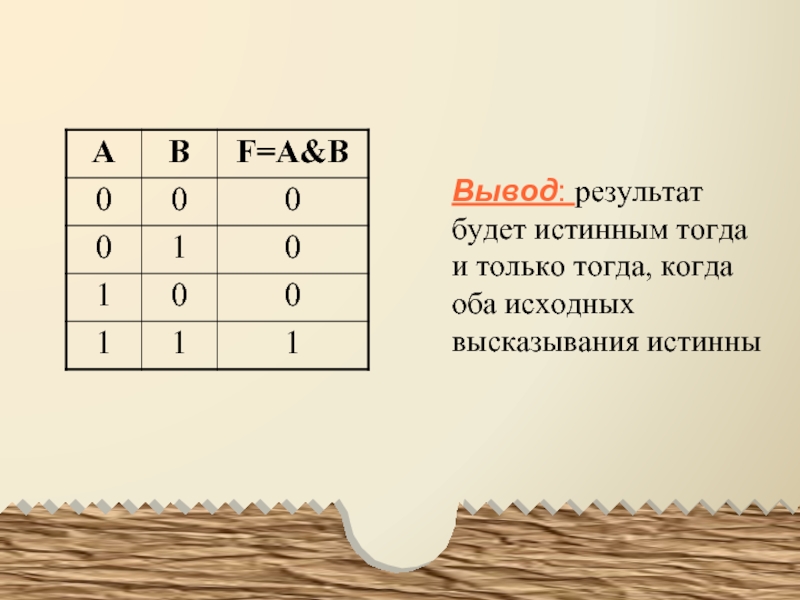
- 4. Вывод: результат будет истинным тогда и только тогда, когда оба исходных высказывания истинны
- 5. Логическая операция ДИЗЪЮНКЦИЯ Название: логическое
- 6. Вывод: результат будет ложным тогда и только
- 7. Логическая операция ИНВЕРСИЯ Название: отрицание
- 8. Вывод: результат будет ложным, если исходное выражение истинно, и наоборот
- 9. Логическая операция ИМПЛИКАЦИЯ Название:
- 10. Логическая операция ЭКВИВАЛЕНТНОСТЬ Название: логическое равенство
Слайд 2Таблица истинности – таблица, определяющая значение сложного высказывания при всех возможных
значениях простых высказываний
Слайд 3Логическая операция КОНЪЮНКЦИЯ
Название: логическое умножение
обозначение &, ^ (А&В или А^В
);
соответствует союзу и (А и В );
В алгебре множеств конъюнкции соответствует операция пересечения множеств, то есть множеству, получившемуся в результате умножения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
соответствует союзу и (А и В );
В алгебре множеств конъюнкции соответствует операция пересечения множеств, то есть множеству, получившемуся в результате умножения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Слайд 4Вывод: результат будет истинным тогда и только тогда, когда оба исходных
высказывания истинны
Слайд 5Логическая операция ДИЗЪЮНКЦИЯ
Название: логическое сложение
обозначение v (АvВ);
соответствует союзу или
(А или В );
В алгебре множеств дизъюнкции соответствует операция объединения множеств, то есть множеству, получившемуся в результате сложения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
В алгебре множеств дизъюнкции соответствует операция объединения множеств, то есть множеству, получившемуся в результате сложения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
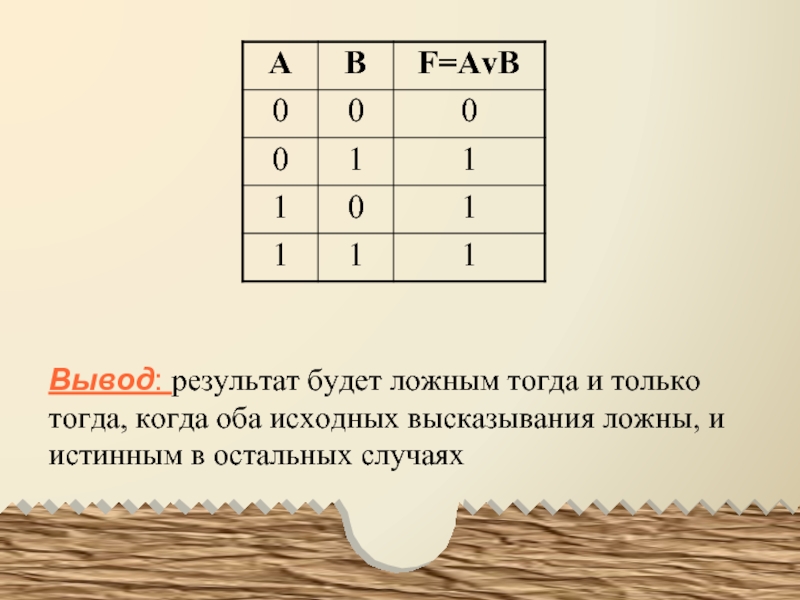
Слайд 6Вывод: результат будет ложным тогда и только тогда, когда оба исходных
высказывания ложны, и истинным в остальных случаях
Слайд 7Логическая операция ИНВЕРСИЯ
Название: отрицание
Обозначение: (¬А или );
соответствует
союзу неверно, что… и частице не (Не А);
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, то есть множеству, получившемуся в результате отрицания множества А, соответствует множество ¬А, дополняющее его до универсального множества.
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, то есть множеству, получившемуся в результате отрицания множества А, соответствует множество ¬А, дополняющее его до универсального множества.
¬А
А
Слайд 9Логическая операция ИМПЛИКАЦИЯ
Название: логическое следование
Обозначение: → или => (А=>В,
А – условие,
В - следствие).
соответствует союзу: если ..., то ... (Если А, то В; когда А, тогда В; коль скоро А то и В)
В - следствие).
соответствует союзу: если ..., то ... (Если А, то В; когда А, тогда В; коль скоро А то и В)
Слайд 10Логическая операция ЭКВИВАЛЕНТНОСТЬ
Название: логическое равенство
Обозначения ↔ или ~ (А↔ В
или А=В).
соответствует союзу: тогда и только тогда; в том и только в том случае (А тогда и только тогда, когда В)
соответствует союзу: тогда и только тогда; в том и только в том случае (А тогда и только тогда, когда В)