- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейное программирование презентация
Содержание
- 1. Линейное программирование
- 2. Задача линейного программирования – 3 слайд. Геометрический
- 3. Задача линейного программирования (ЛП) Задачи ЛП – самая обширная часть оптимизационных (примерно 70%)
- 4. Этапы построения математической модели Определение переменных задачи.
- 5. Классические задачи линейного программирования Задача технического контроля
- 6. Задача технического контроля Примечание: ОТК – Отдел Технического Контроля
- 7. В ОТК некоторой фирмы работают контролеры 1
- 9. Построение модели
- 10. Построение модели
- 11. 3. Задание целевой функции
- 12. Вся задача технического контроля может быть сформулирована следующим образом.
- 13. Транспортная задача Или задача о рациональном перевозе однородных продуктов из пунктов производства в пункты потребления.
- 14.
- 15. Математическая модель задачи
- 16. Задача о диете Или задача о составлении рациона
- 17.
- 18. Математическая модель задачи
- 19. Задача об использовании сырья
- 20.
- 21. Исходные данные задачи Представим исходные данные в виде таблицы
- 22.
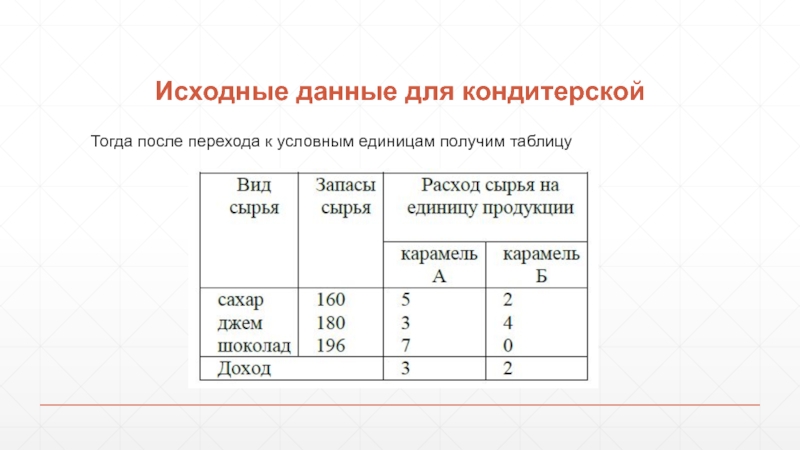
- 23. Исходные данные для кондитерской Тогда после перехода к условным единицам получим таблицу
- 24. Математическая модель задачи
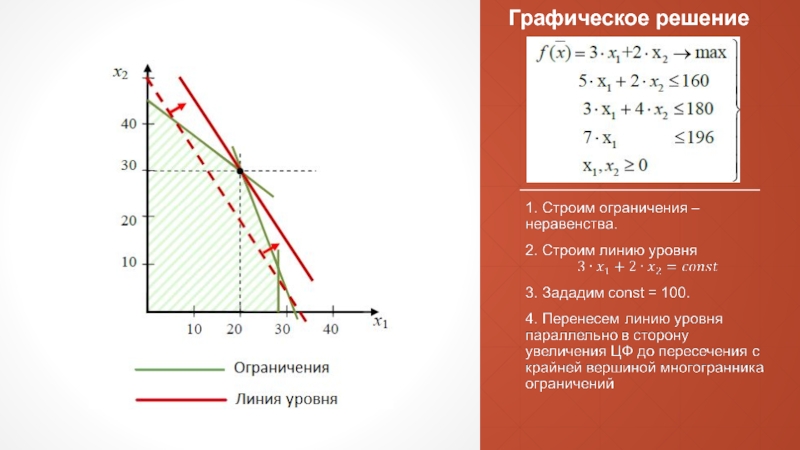
- 25. Графическое решение
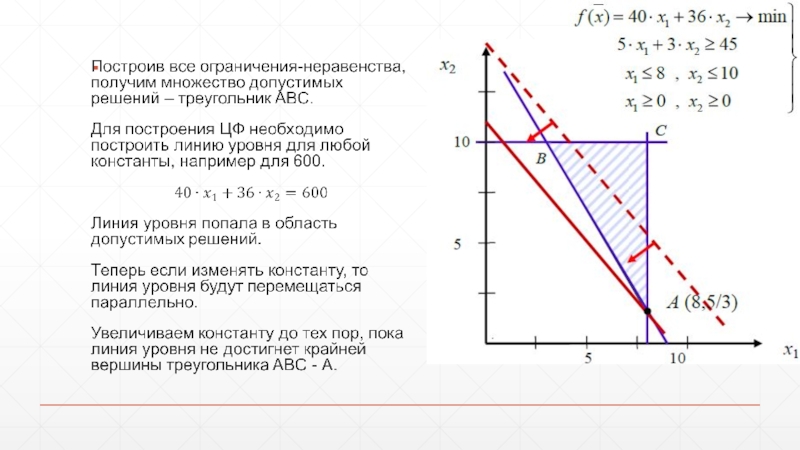
- 26. Геометрический метод решения ЗЛП Решим геометрическим методом задачу технического контроля:
- 27.
- 28.
- 29. Частные случаи геометрических решений
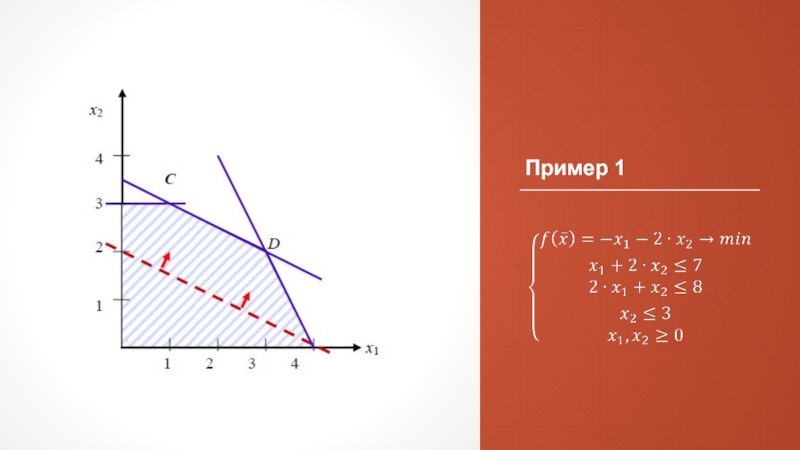
- 30. Пример 1
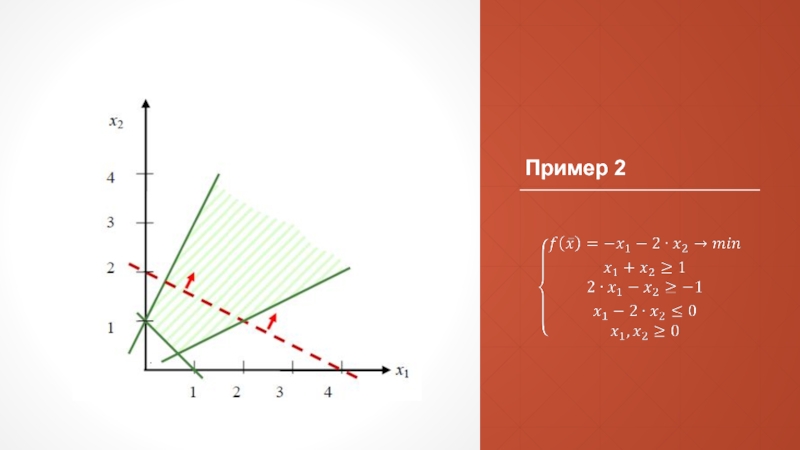
- 31. Пример 2
- 32. Задача линейного программирования в стандартной форме
- 33.
- 34. Матрично–векторная запись
- 35. Приведение ЗЛП к стандартному виду
- 36. Преобразования неравенств
- 37. Преобразования неравенств Преобразуем неравенства из задачи об
- 38. Приведение ЗЛП к стандартному виду
- 39. Приведение ЗЛП к стандартному виду
- 40. Пример приведения ЗЛП к стандартному виду
- 41. Перепишем задачу ЛП с учетом новых переменных и замен:
- 42. Симплекс метод решения ЗЛП
- 43. Запишем задачу линейного программирования в стандартной форме
- 44. Метод Гаусса – Жордана Основная идея метода
- 45. Базисные и свободные переменные
- 46. Выразим из предыдущей системы базисные переменные:
- 47. Базисное решение Опорный план vbnvbg
- 48. Метод последовательного исключения переменных (метод Гаусса) Метод
- 49. Прямой ход
- 50. Прямой ход
- 51. Обратный ход
- 52. Пример решения СЛАУ методом Гаусса
- 53.
- 54. Метод главных элементов Применяется в случаях, когда
- 55. Основная идея метода главных элементов
- 56. Основная идея метода главных элементов В
- 57. Пример решения СЛАУ методом Гаусса с выбором главного элемента
- 58. Симплекс метод
- 59. Алгоритм симплекс метода Выбор начального опорного плана.
- 60. Смежный опорный план Смежным опорным планом называют
- 61. Составим симплекс – таблицу для задачи использования
- 62. Начальный опорный план
- 63. I. Нахождение начального опорного плана
- 64. II. Нахождение смежного опорного плана Необходимо одну
- 65.
- 66. Лемма 1
- 67. Лемма 2
- 68.
- 69. III. Приведение системы к каноническому виду
- 70. Шаг 1
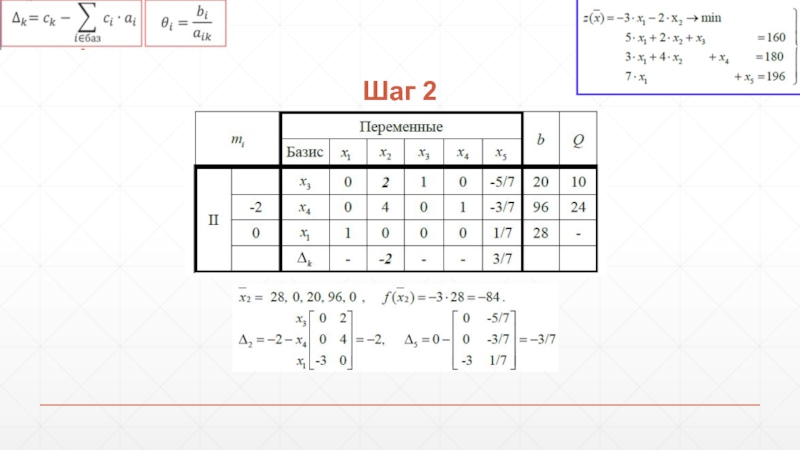
- 71. Шаг 2
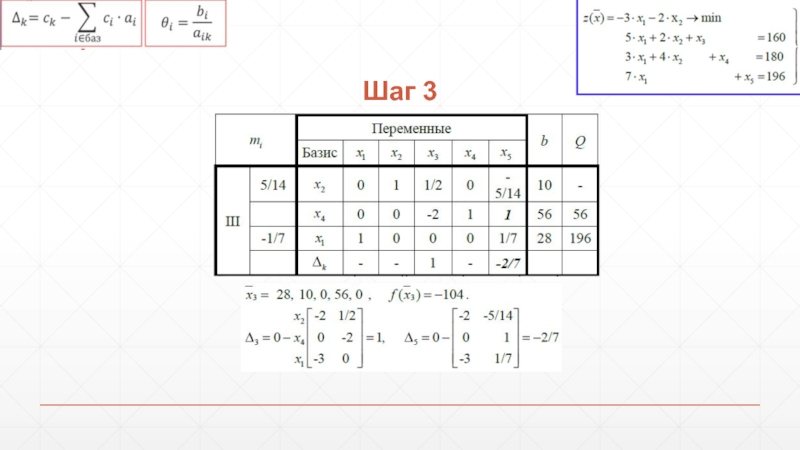
- 72. Шаг 3
- 73. Шаг 4
- 74. Полная симплекс таблица
- 75. Замечание
- 76. Метод искусственного базиса
- 77.
- 78.
- 79. Пример
- 80.
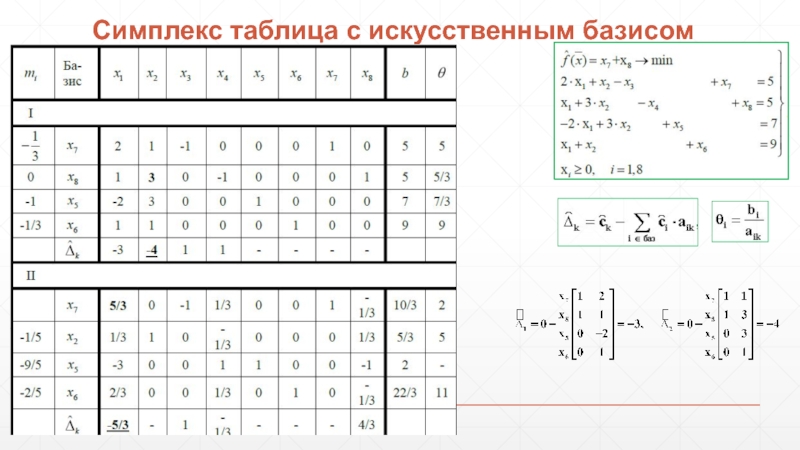
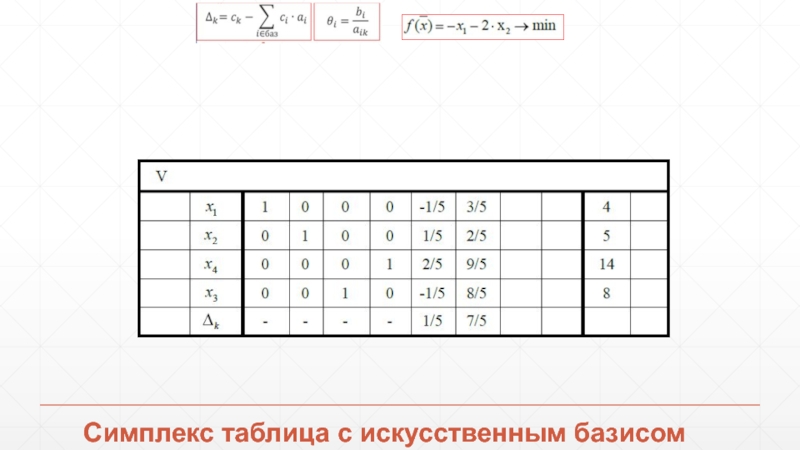
- 81. Симплекс таблица с искусственным базисом
- 82. Симплекс таблица с искусственным базисом
- 83. Симплекс таблица с искусственным базисом
- 84.
- 85. Этапы метода искусственного базиса
- 86. Этапы метода искусственного базиса
- 87.
- 88. Двойственность задач линейного программирования
- 89. Определение двойственности Для любой задачи линейного программирования
- 90. Прямая и двойственная задачи
- 91. Теорема 1
- 92. Теорема 2
- 93. Сравнение прямой и двойственной задачи
- 94. В исходной задаче В двойственной
- 95. Число ограничений и переменных В исходной задаче
- 96. Правые части ограничений – это коэффициенты целевой функции двойственной задачи
- 97. Знаки ограничений и цель задачи меняются на противоположные В исходной задаче В двойственной
- 98. Соответствие двойственных задач ЛП
- 99. Пример
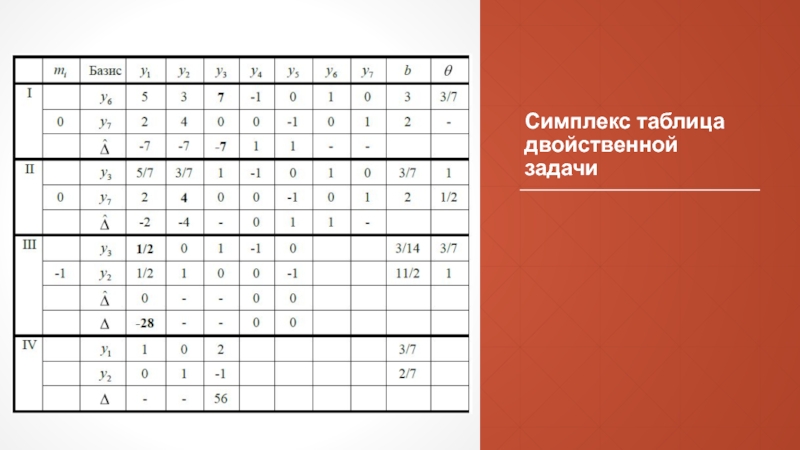
- 100. Симплекс таблица двойственной задачи
- 101. Таким образом, получен следующий оптимальный план двойственной
- 102.
- 103. Экономическая трактовка двойственности Если прямую задачу:
- 104. Экономический смысл переменных
- 105. Тогда стоимость всех ресурсов А
- 106.
Слайд 2Задача линейного программирования – 3 слайд.
Геометрический метод решения ЗЛП – 26
слайд.
Задача линейного программирования в стандартной форме – 32 слайд.
Симплексный метод решения ЗЛП – 42 слайд.
Метод Гаусса – 48 слайд.
Симплекс метод – 58 слайд.
Метод искусственного базиса – 76 слайд.
Двойственность задач линейного программирования – 87 слайд.
Задача линейного программирования в стандартной форме – 32 слайд.
Симплексный метод решения ЗЛП – 42 слайд.
Метод Гаусса – 48 слайд.
Симплекс метод – 58 слайд.
Метод искусственного базиса – 76 слайд.
Двойственность задач линейного программирования – 87 слайд.
Оглавление
Слайд 3Задача линейного программирования (ЛП)
Задачи ЛП – самая обширная часть оптимизационных (примерно
70%)
Слайд 4Этапы построения математической модели
Определение переменных задачи.
Представление ограничений в виде линейных уравнений
или неравенств.
Задание линейной целевой функции и смысла оптимизации.
Задание линейной целевой функции и смысла оптимизации.
Слайд 5Классические задачи линейного программирования
Задача технического контроля (слайд 6);
Транспортная задача (слайд 13
);
Задача о диете (слайд 16);
Задача об использовании сырья (слайд 19).
Задача о диете (слайд 16);
Задача об использовании сырья (слайд 19).
Слайд 7В ОТК некоторой фирмы работают контролеры 1 и 2 разрядов (К1
и К2);
Норма выработки ОТК за 8 часов (раб. день) составляет не менее 1800 изделий;
К1 проверяет 25 изделий/час (точность 98%);
К2 проверяет 15 изделий/час (точность 95%);
Заработная плата К1 равна 4$ / час;
Заработная плата К2 равна 3$ / час;
При каждой ошибке контролера фирма несет убыток в 2$;
Фирма может использовать не более 8 - К1 и 10 - К2;
Определить оптимальный состав ОТК,
при котором общие затраты на контроль будут минимальны.
Норма выработки ОТК за 8 часов (раб. день) составляет не менее 1800 изделий;
К1 проверяет 25 изделий/час (точность 98%);
К2 проверяет 15 изделий/час (точность 95%);
Заработная плата К1 равна 4$ / час;
Заработная плата К2 равна 3$ / час;
При каждой ошибке контролера фирма несет убыток в 2$;
Фирма может использовать не более 8 - К1 и 10 - К2;
Определить оптимальный состав ОТК,
при котором общие затраты на контроль будут минимальны.
Слайд 13Транспортная задача
Или задача о рациональном перевозе однородных продуктов из пунктов производства
в пункты потребления.
Слайд 37Преобразования неравенств
Преобразуем неравенства из задачи об использовании сырья добавив во все
три уравнения остаточную переменную.
Слайд 43Запишем задачу линейного программирования в стандартной форме в развернутом виде:
Число уравнений
системы меньше числа неизвестных (m < n).
Слайд 44Метод Гаусса – Жордана
Основная идея метода состоит в сведении m уравнения
с n неизвестными к каноническому или ступенчатому виду, путем линейных преобразования над строками (сложение строк и умножение на скаляр).
Это позволяет привести СЛАУ к следующему виду:
Это позволяет привести СЛАУ к следующему виду:
Слайд 46Выразим из предыдущей системы базисные переменные:
Из этой системы можно получить решение
для базисных переменных, присваивая независимым переменным произвольные значения
Слайд 48Метод последовательного исключения переменных (метод Гаусса)
Метод Гаусса состоит из двух этапов:
Прямой
ход
Обратный ход
Цель прямого хода - приведение матрицы системы A к верхнетреугольному виду.
Обратный ход
Цель прямого хода - приведение матрицы системы A к верхнетреугольному виду.
Слайд 54Метод главных элементов
Применяется в случаях, когда главные диагональные элементы системы уравнений
в результате преобразований получаются нулевые.
В этих условиях схема единственного деления становится неработоспособной, так как на главные элементы в ходе преобразований производится деление.
В этих условиях схема единственного деления становится неработоспособной, так как на главные элементы в ходе преобразований производится деление.
Слайд 56Основная идея метода главных элементов
В результате составляем новую систему уравнений
из вычеркнутых строк. Полученная матрица не треугольного вида, как в схеме единственного деления Гаусса. Но каждое уравнение содержит разное количество неизвестных:
в последнем уравнении – 1 неизвестное;
в (n-1)-м –2 неизвестных и т.д.;
в первом уравнении – все n неизвестных.
Такой вид преобразованной системы позволяет последовательно находить неизвестные, начиная с последнего уравнения.
в последнем уравнении – 1 неизвестное;
в (n-1)-м –2 неизвестных и т.д.;
в первом уравнении – все n неизвестных.
Такой вид преобразованной системы позволяет последовательно находить неизвестные, начиная с последнего уравнения.
Слайд 59Алгоритм симплекс метода
Выбор начального опорного плана.
Переход от начального опорного плана к
другому опорному плану с лучшим значением целевой функции. (!Смежному). Приведение системы, для смежного опорного плана к каноническому виду
Продолжение поиска опорного плана улучшающего целевую функцию до достижения оптимального плана..
Продолжение поиска опорного плана улучшающего целевую функцию до достижения оптимального плана..
Слайд 60Смежный опорный план
Смежным опорным планом называют план, отличающийся от текущего лишь
одной переменной.
Для получения смежного опорного плана одну базисную переменную превращают в свободную, а эту свободную вводят в базисные переменные.
Основной здесь вопрос – какую переменную выбрать, чтобы целевая функция уменьшалась?
Для получения смежного опорного плана одну базисную переменную превращают в свободную, а эту свободную вводят в базисные переменные.
Основной здесь вопрос – какую переменную выбрать, чтобы целевая функция уменьшалась?
Слайд 61Составим симплекс – таблицу для задачи использования ресурсов.
Для этого
запишем
- задачу в каноническом виде и
заменим - цель поиска максимум на минимум.
заменим - цель поиска максимум на минимум.
Слайд 64II. Нахождение смежного опорного плана
Необходимо одну переменную из свободных перевести в
базис, так, чтобы целевая функция уменьшалась.
Для удобства запишем ЗЛП в стандартной векторно-матричной форме:
Для удобства запишем ЗЛП в стандартной векторно-матричной форме:
Слайд 89Определение двойственности
Для любой задачи линейного программирования существует некоторая другая задача линейного
программирования, решение которой тесно связано с решением исходной.
Таким образом, двойственность состоит в существовании пары задач:
прямая задача;
двойственная задача.
Таким образом, двойственность состоит в существовании пары задач:
прямая задача;
двойственная задача.
Слайд 95Число ограничений и переменных
В исходной задаче
n – переменных;
m – ограничений.
В двойственной
m
– переменных;
n – ограничений.
n – ограничений.
Слайд 101Таким образом, получен следующий оптимальный план двойственной задачи:
Для получения оптимального решения
прямой задачи воспользуемся соотношением из Теоремы 2:
Слайд 103Экономическая трактовка двойственности
Если прямую задачу:
рассматривать, как задачу об использовании сырья (ресурсов),
то параметры задачи имеют следующий экономический смысл.
Слайд 105Тогда стоимость всех ресурсов
А стоимость всех затраченных ресурсов, идущих на выпуск
единицы j-ой продукции не меньше окончательной стоимости этого продукта