Алгоритмы,формулы и рисунки
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Лекция 6. Сетевые методы и графы в автоматизированном управлении презентация
Содержание
- 1. Лекция 6. Сетевые методы и графы в автоматизированном управлении
- 2. Ориентированный эйлеров граф Теорема, сформулированная для
- 3. Ориентированный гамильтонов граф Сильносвязный полный ориентированный граф является гамильтоновым
- 4. Ациклический ориентированный граф По отношению
- 5. Топологическая сортировка Теорема: в ациклическом ориентированном графе
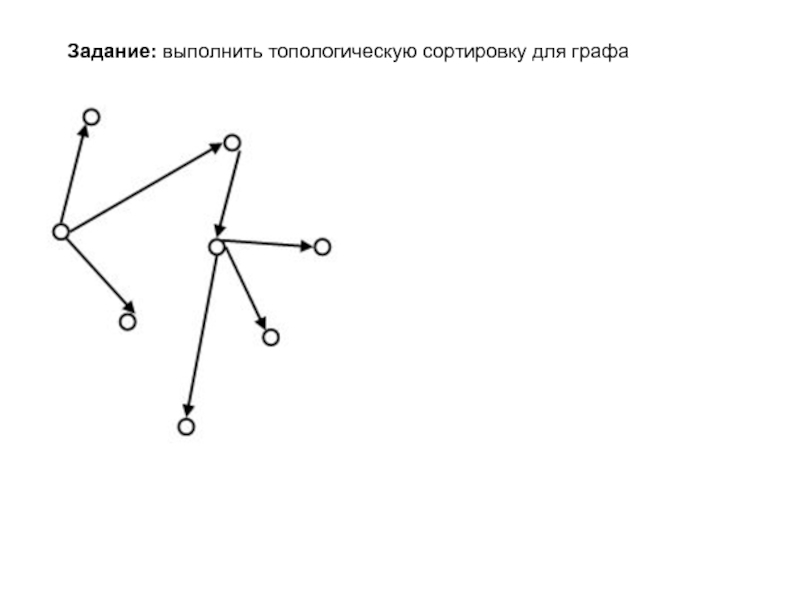
- 6. Задание: выполнить топологическую сортировку для графа
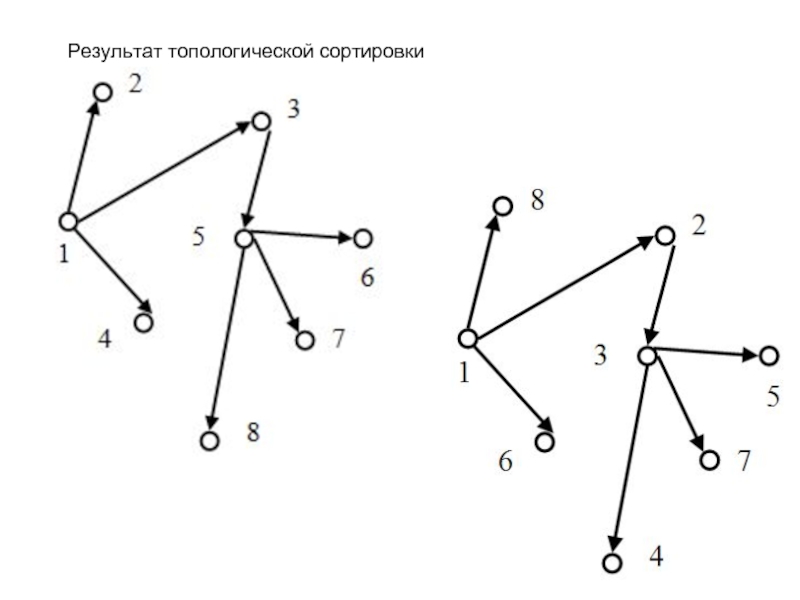
- 7. Результат топологической сортировки
- 8. Матрица смежности ориентированного графа Пусть G=(V, E)
- 9. Матрица смежности неориентированного графа В случае неориентированного
- 10. Матрицей смежности несвязного графа является нулевая матрица порядка n×n
- 11. Матрица достижимостей R=[rij] Все диагональные элементы
- 12. Вопрос 1. Как будет выглядеть матрица достижимости
- 13. Матрица инциденций B=[bij] Если граф G
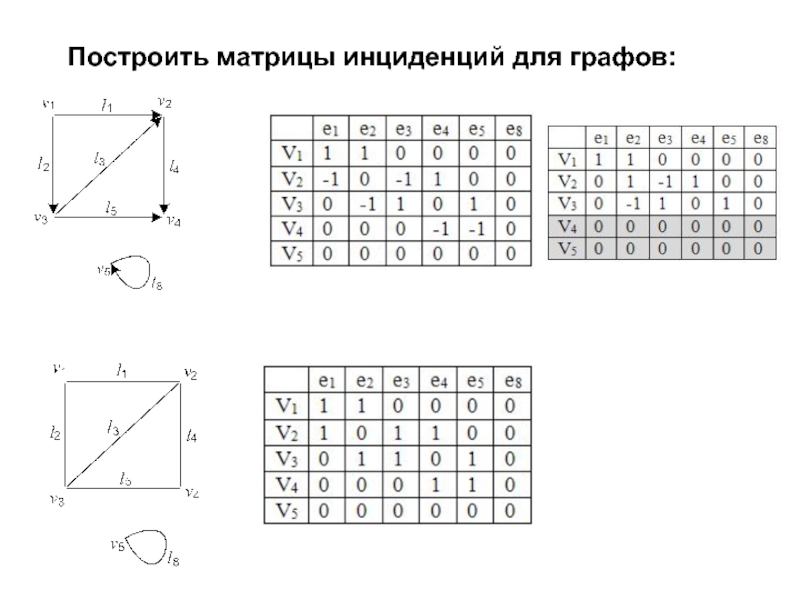
- 14. Построить матрицы инциденций для графов:
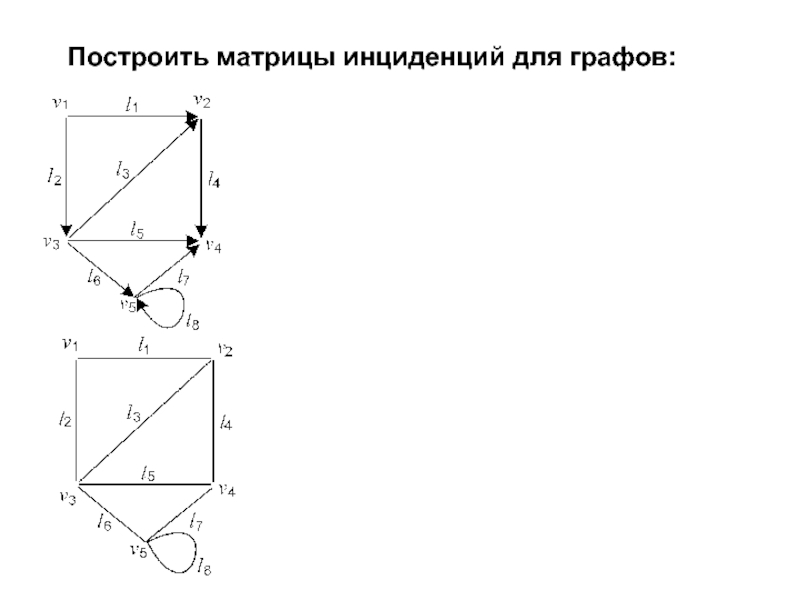
- 15. Построить матрицы инциденций для графов:
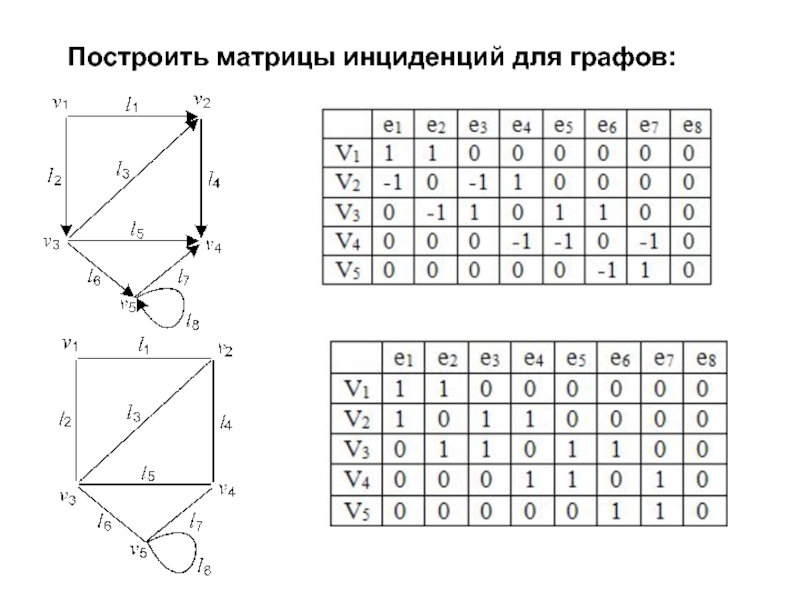
- 16. Свойства матриц инциденций для графов:
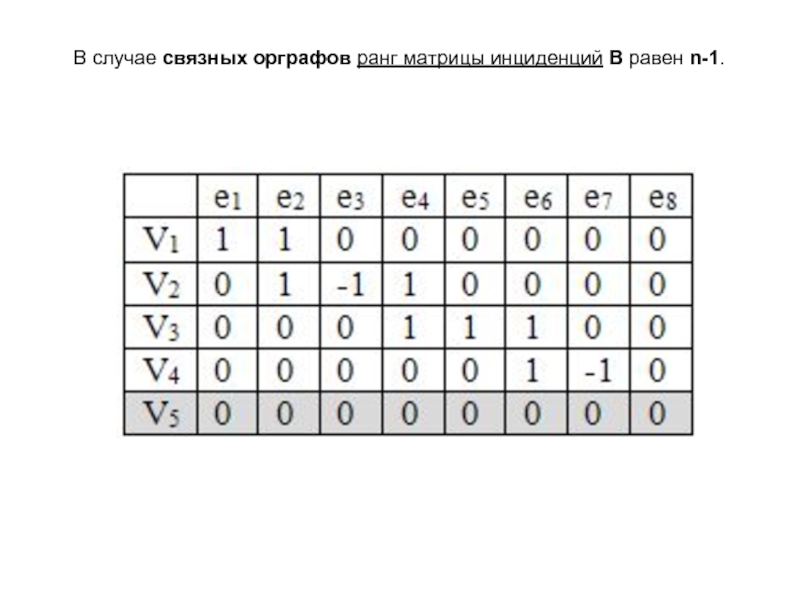
- 17. В случае связных орграфов ранг матрицы инциденций В равен n-1.
- 18. Построить матрицы инциденций для графов:
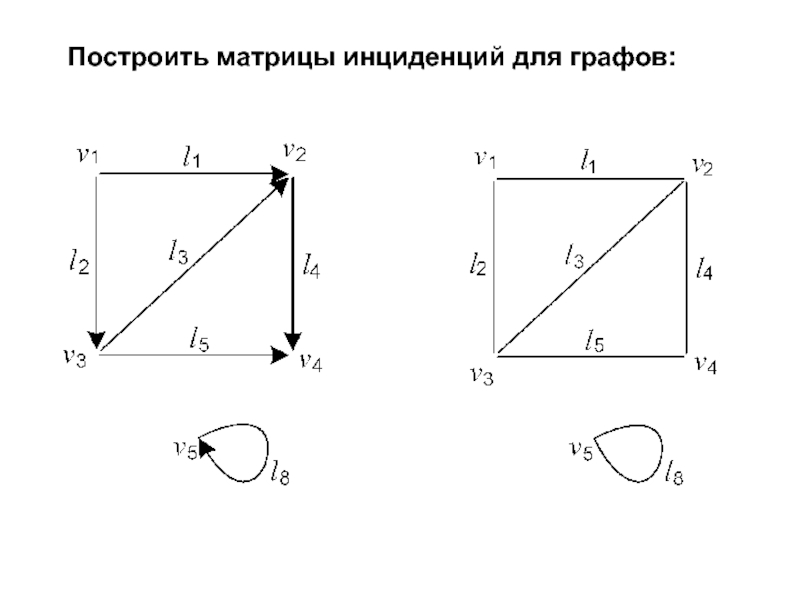
- 19. Построить матрицы инциденций для графов:
Слайд 1Лекция 6 – по курсу «Сетевые методы и графы в автоматизированном
Слайд 2
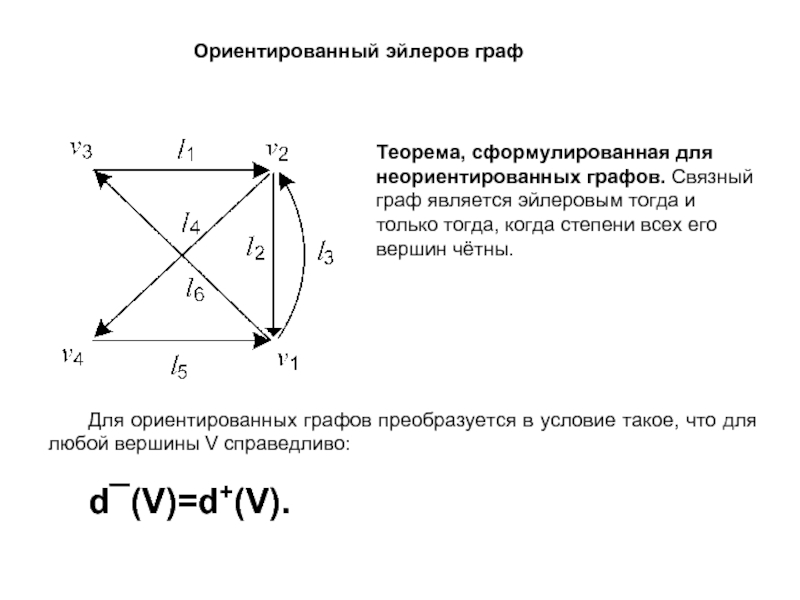
Ориентированный эйлеров граф
Теорема, сформулированная для неориентированных графов. Связный граф является эйлеровым
Для ориентированных графов преобразуется в условие такое, что для любой вершины V справедливо:
d¯(V)=d+(V).
Слайд 3
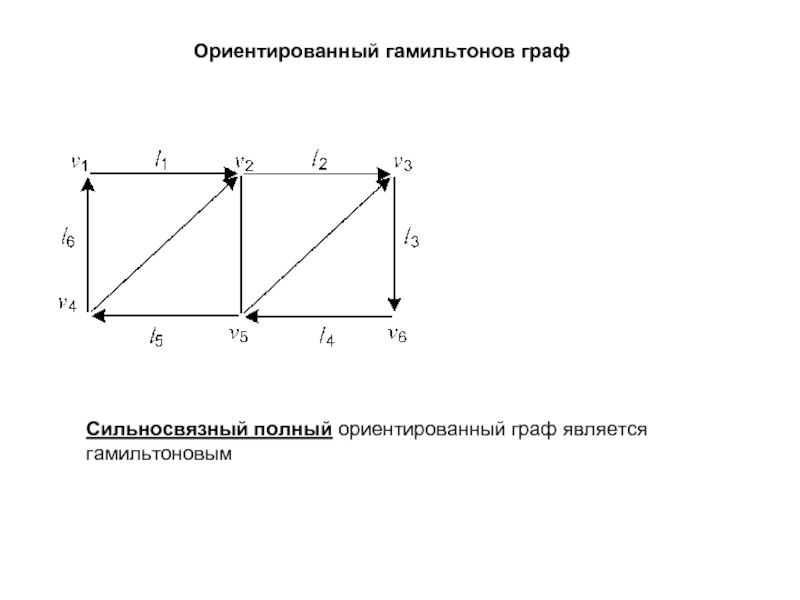
Ориентированный гамильтонов граф
Сильносвязный полный ориентированный граф является гамильтоновым
Слайд 4
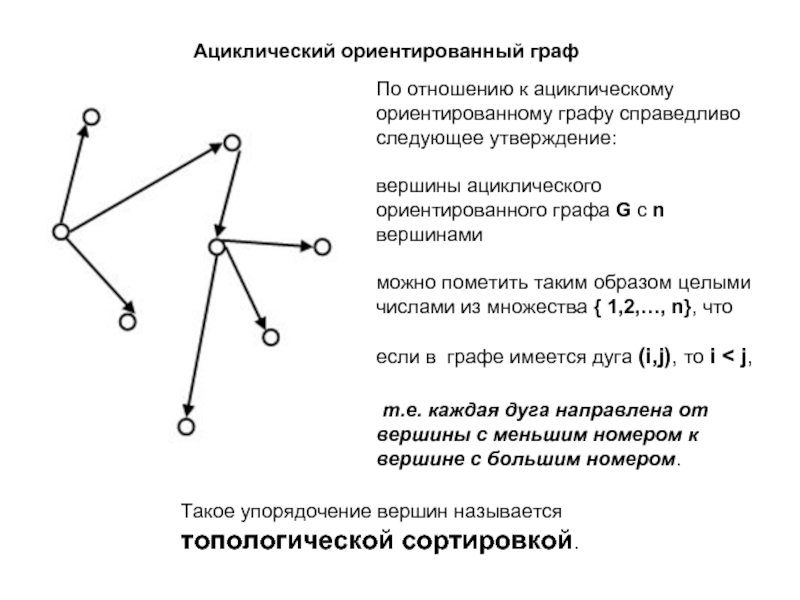
Ациклический ориентированный граф
По отношению к ациклическому ориентированному графу справедливо следующее утверждение:
вершины ациклического ориентированного графа G с n вершинами
можно пометить таким образом целыми числами из множества { 1,2,…, n}, что
если в графе имеется дуга (i,j), то i < j,
т.е. каждая дуга направлена от вершины с меньшим номером к вершине с большим номером.
Такое упорядочение вершин называется
топологической сортировкой.
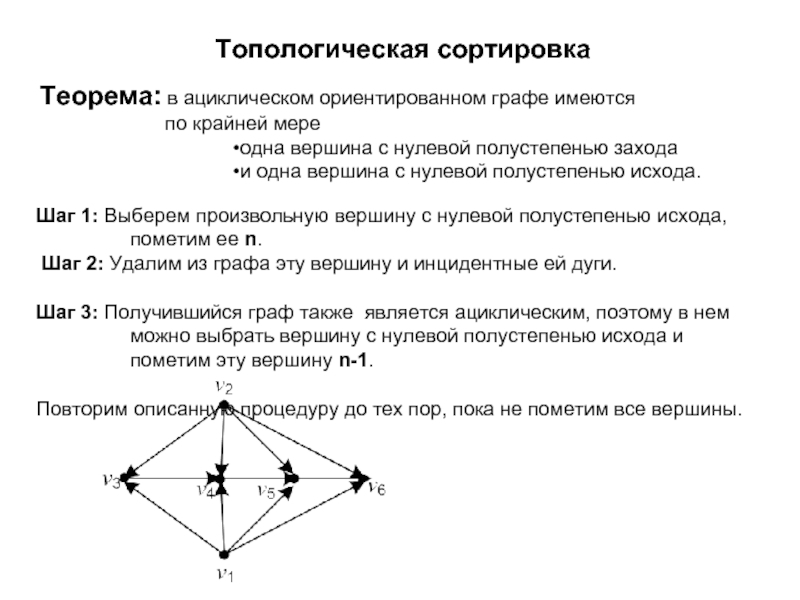
Слайд 5Топологическая сортировка
Теорема: в ациклическом ориентированном графе имеются
по крайней мере
одна
и одна вершина с нулевой полустепенью исхода.
Шаг 1: Выберем произвольную вершину с нулевой полустепенью исхода, пометим ее n.
Шаг 2: Удалим из графа эту вершину и инцидентные ей дуги.
Шаг 3: Получившийся граф также является ациклическим, поэтому в нем можно выбрать вершину с нулевой полустепенью исхода и пометим эту вершину n-1.
Повторим описанную процедуру до тех пор, пока не пометим все вершины.
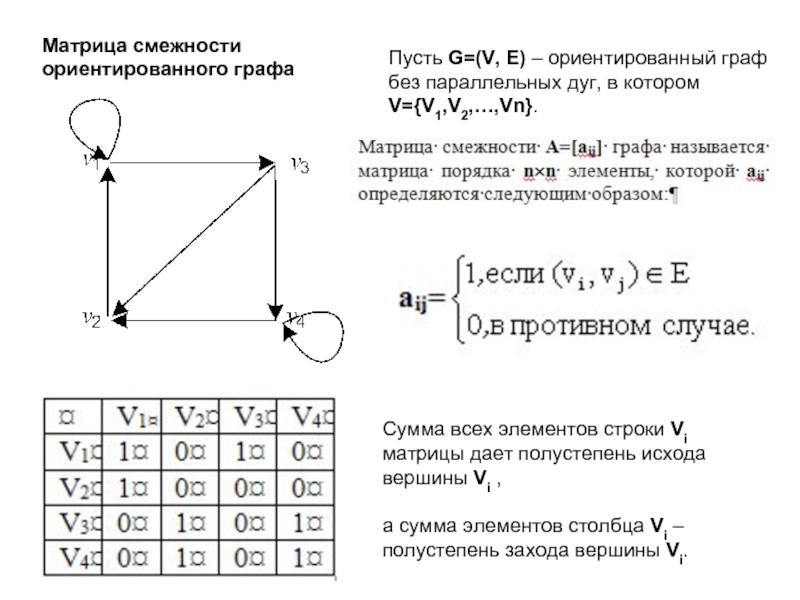
Слайд 8Матрица смежности ориентированного графа
Пусть G=(V, E) – ориентированный граф без параллельных
Сумма всех элементов строки Vi матрицы дает полустепень исхода вершины Vi ,
а сумма элементов столбца Vi – полустепень захода вершины Vi.
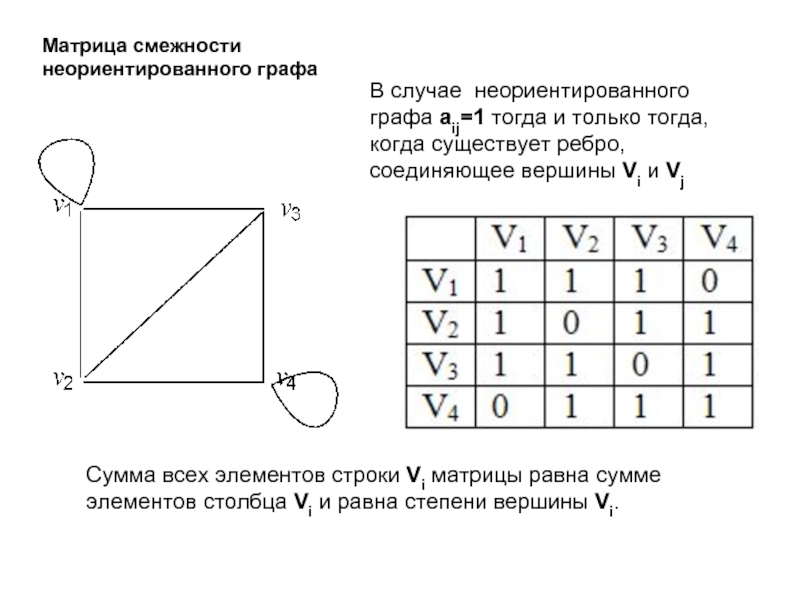
Слайд 9Матрица смежности неориентированного графа
В случае неориентированного графа aij=1 тогда и только
Сумма всех элементов строки Vi матрицы равна сумме элементов столбца Vi и равна степени вершины Vi.
Слайд 11Матрица достижимостей R=[rij]
Все диагональные элементы в матрице R равны 1,
Слайд 12Вопрос 1. Как будет выглядеть матрица достижимости для неоринтированного графа?
Вопрос
Слайд 13Матрица инциденций B=[bij]
Если граф G ориентированный
Если граф G неориентированный
Рассмотрим граф
Слайд 16Свойства матриц инциденций для графов:
Свойства матрицы инцидентности неориентированного графа.
1. Сумма элементов
2. Сумма элементов матрицы по i-му столбцы равна 2.
Свойства матрици инцидентности орграфа.
Сумма строк матрицы B(G) является нулевой строкой.
Любая строка матрицы B(G) является линейной комбинацией остальных строк.
Ранг матрицы B(G) равен p-1.


![Матрица достижимостей R=[rij] Все диагональные элементы в матрице R равны 1, поскольку каждая вершина достижима](/img/tmb/1/4860/5f3bf059f60bec1710e8a52b8d9104bf-800x.jpg)

![Матрица инциденций B=[bij] Если граф G ориентированныйЕсли граф G неориентированныйРассмотрим граф G на n вершинах](/img/tmb/1/4860/541dc51a062839f1451fb0555de82066-800x.jpg)