- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
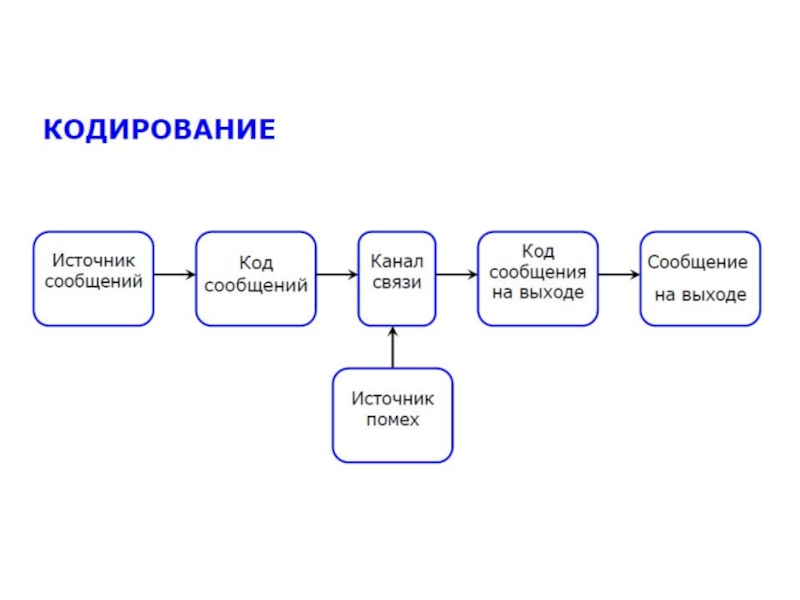
Лекция 4-2. Основные понятия теории кодирования презентация
Содержание
- 2. Основные понятия теории кодирования
- 5. Проблема распознавания взаимной однозначности кодирования
- 6. Теорема 3.2.1. Если схема обладает свойством префикса,
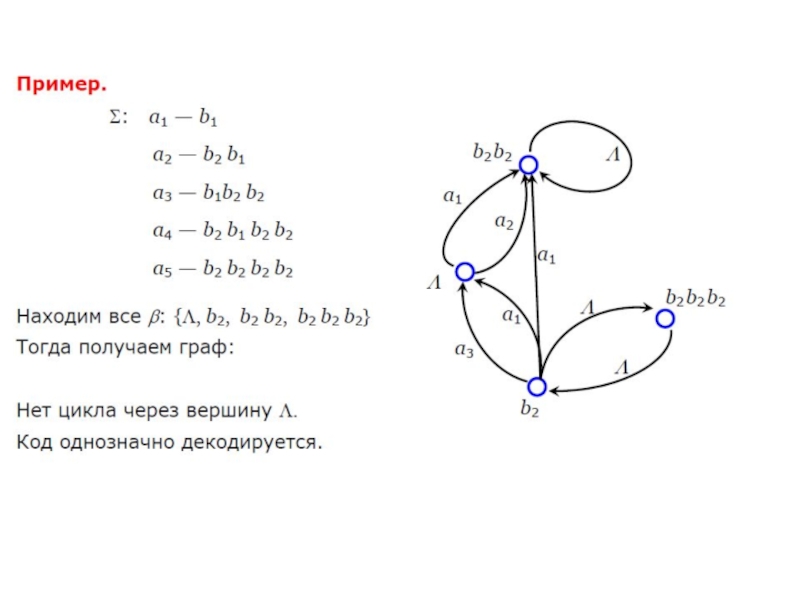
- 8. Алгоритм проверки однозначности кодирования
- 12. Теорема Маркова о взаимной однозначности алфавитного кодирования:
- 13. Доказательство. Пусть ϕ не является взаимно
- 14. Лемма. Если — неприводимое слово,
- 15. Слова из второго класса разбивают слово не
Слайд 6Теорема 3.2.1. Если схема обладает свойством префикса, то алфавитное
кодирование является взаимно-однозначным.
Таким
однозначности.
Слайд 12Теорема Маркова о взаимной однозначности алфавитного кодирования:
Пусть
— некоторое кодирование. Пусть W
Тогда если кодирование φ не взаимно однозначно, то существуют два различных слова
Слайд 13Доказательство.
Пусть ϕ не является взаимно однозначным. Тогда существует некоторое слово
Слова нового разбиения разделим на два класса: к I классу отнесём слова, являющиеся элементарными кодами, а ко II классу — все остальные слова (то есть слова, являющиеся началами кодовых слов одного разбиения и концами слов второго разбиения).
Слайд 14Лемма. Если — неприводимое слово, то все слова β1,
Доказательство. Пусть β' = β''. Тогда, очевидно, слово не будет неприводимым, поскольку при выкидывании отрезка между β' и β'', вместе с любым из этих слов, получим снова две различные расшифровки этого слова (проверьте). Лемма доказана.
Таким образом, все β1, β2, …, βm разные. Тогда число слов второго класса не превосходит числа непустых начал элементарных кодов, то есть не превосходит
Слайд 15Слова из второго класса разбивают слово не более чем на L
а в каждом из них укладывается слов не более чем W + 1. Отсюда число кодовых слов в любом разбиении не превосходит
а поскольку число целое, то не превосходит и целой части
Теорема доказана.