- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Квантование. Дискретная случайная величина презентация
Содержание
- 1. Квантование. Дискретная случайная величина
- 2. Квантование Дискретная случайная величина –
- 3. Виды сообщений 1) Непрерывные по множеству
- 4. Виды сообщений 2) Дискретные по множеству
- 5. Виды сообщений 3) Непрерывные по времени
- 6. Виды сообщений 4) Непрерывные по множеству
- 7. Квантование по уровню Квантование по
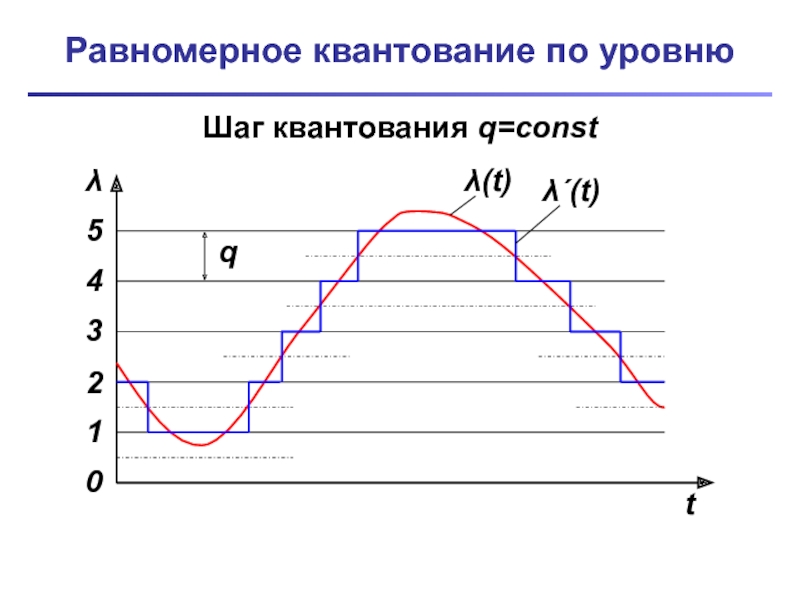
- 8. Равномерное квантование по уровню λ t
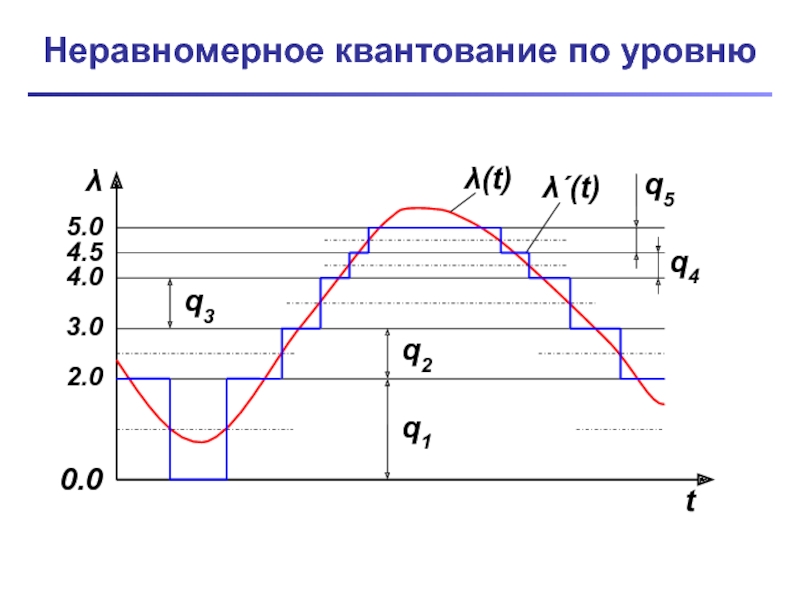
- 9. Неравномерное квантование по уровню λ t
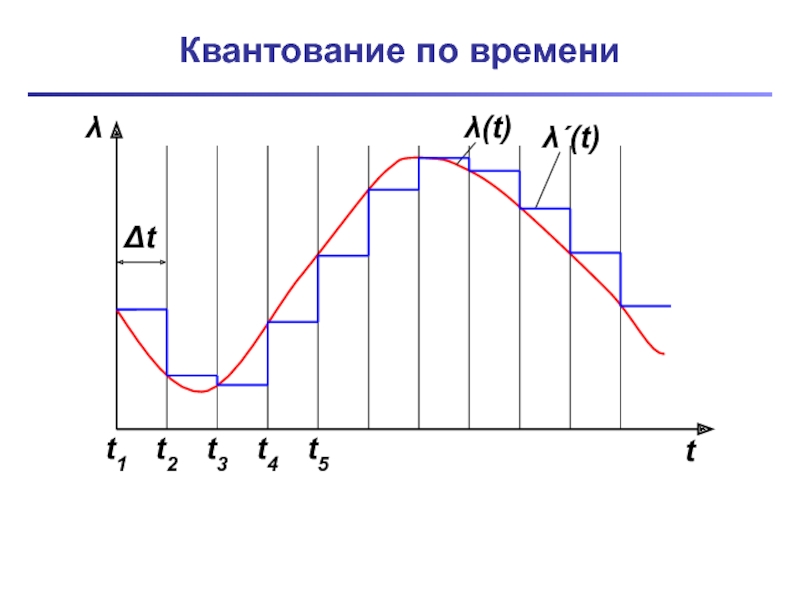
- 10. Квантование по времени Квантование
- 11. Квантование по времени
- 12. Квантование по уровню и времени
Квантование Дискретная случайная величина – случайная величина, которая может принимать конечное число значений. Непрерывная случайная величина – случайная величина, которая может принимать бесконечное число значений. Квантование – замена непрерывной
Слайд 2Квантование
Дискретная случайная величина – случайная величина, которая может принимать конечное число
значений.
Непрерывная случайная величина – случайная величина, которая может принимать бесконечное число значений.
Квантование – замена непрерывной случайной величины дискретной.
Непрерывная случайная величина – случайная величина, которая может принимать бесконечное число значений.
Квантование – замена непрерывной случайной величины дискретной.
Слайд 3Виды сообщений
1)
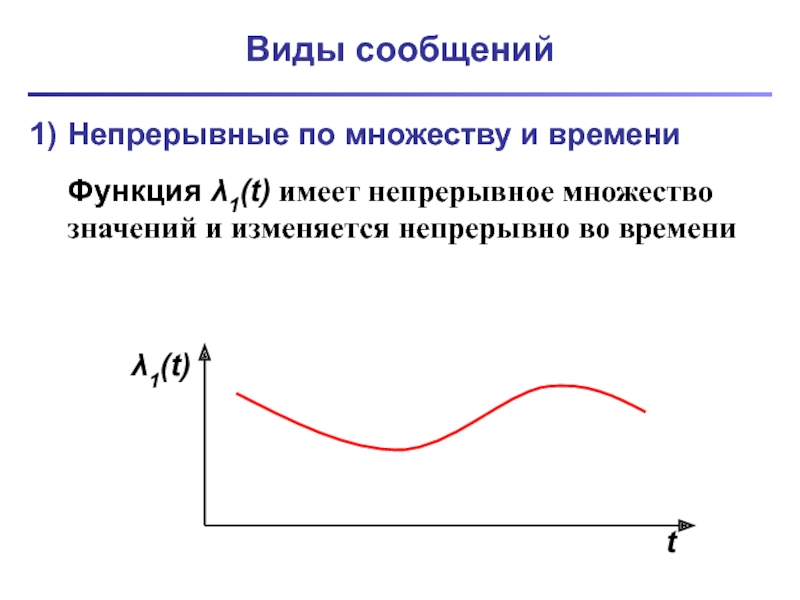
Непрерывные по множеству и времени
Функция λ1(t) имеет непрерывное множество значений
и изменяется непрерывно во времени
Слайд 4Виды сообщений
2)
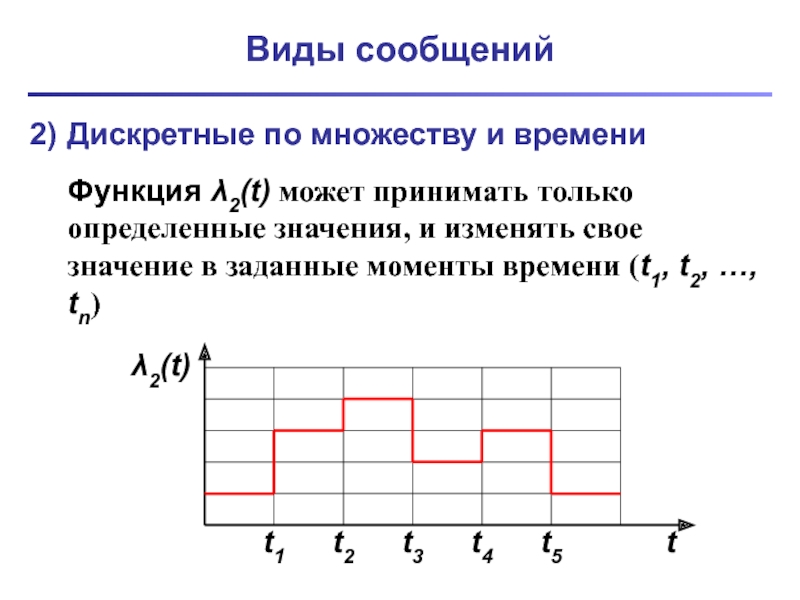
Дискретные по множеству и времени
Функция λ2(t) может принимать только определенные
значения, и изменять свое значение в заданные моменты времени (t1, t2, …, tn)
Слайд 5Виды сообщений
3)
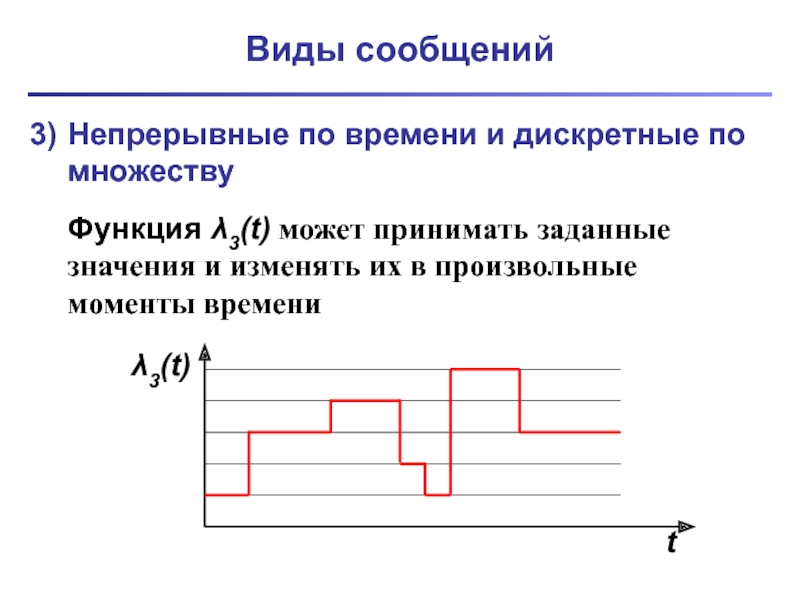
Непрерывные по времени и дискретные по множеству
Функция λ3(t) может принимать
заданные значения и изменять их в произвольные моменты времени
Слайд 6Виды сообщений
4)
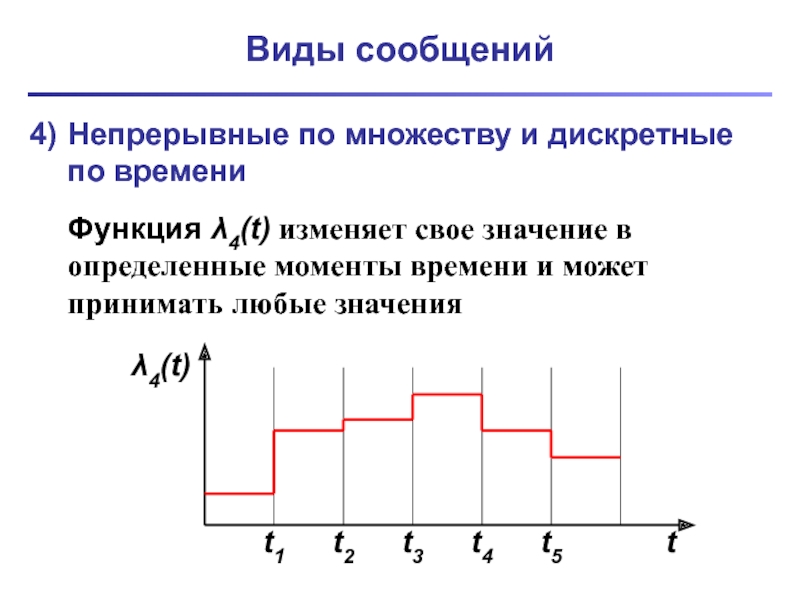
Непрерывные по множеству и дискретные по времени
Функция λ4(t) изменяет свое
значение в определенные моменты времени и может принимать любые значения
Слайд 7Квантование по уровню
Квантование по уровню (квантование по параметру) – процесс замены
непрерывной функции ее отдельными значениями, отстоящими друг от друга на конечный интервал.
Шаг квантования –интервал между двумя дискретными значениями уровней.
Шаг квантования –интервал между двумя дискретными значениями уровней.
Слайд 10Квантование по времени
Квантование по времени (дискретизация) – процесс замены непрерывной функции
ее отдельными значениями в определенные моменты времени.
Слайд 12Квантование по уровню и времени
Квантование по уровню и времени – процесс
замены непрерывной функции ее отдельными значениями, отстоящими друг от друга на конечный интервал, в определенные моменты времени.
