- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Криптографические методы защиты информации. История развития. Современное состояние. Перспективы презентация
Содержание
- 1. Криптографические методы защиты информации. История развития. Современное состояние. Перспективы
- 2. Исторически сложившиеся подходы к защите информации при
- 3. Различие между шифрованием и кодированием Кодирование –
- 4. Правило Керкгоффса «… компрометация системы не должна
- 5. Постулаты разработки криптосистем Противник может иметь в
- 6. Методы криптографии Криптографические алгоритмы: Классическое шифрование Поточные
- 7. Теория секретной связи Клода Шеннона (1944
- 8. Математические модели шифров Модель де Виари
- 9. Шифры Виженера и Бофора (гаммирование таблицей
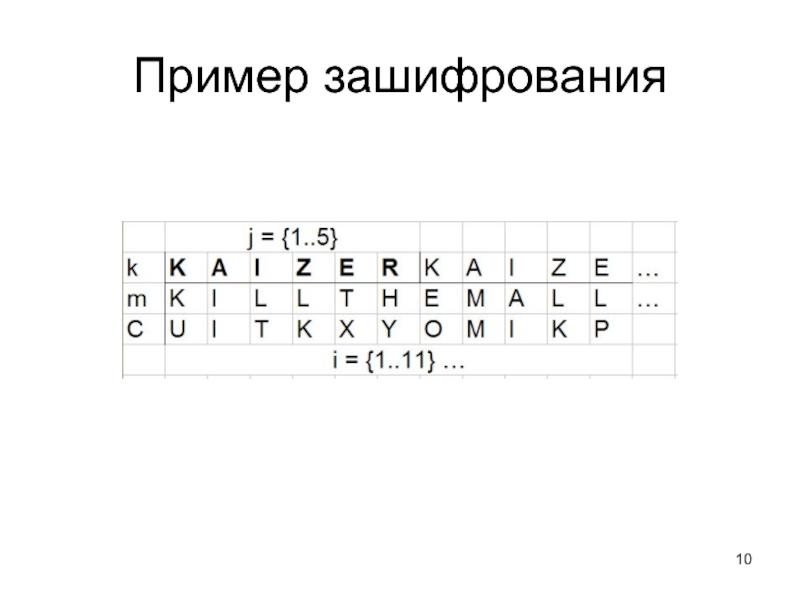
- 10. Пример зашифрования
- 11. Поточные алгоритмы На основе датчиков (генераторов) ИСП
- 12. Поточные алгоритмы на основе РСЛОС РСЛОС конфигурация Фибоначчи РСЛОС конфигурация Галуа Характеристический многочлен
- 14. Поточные алгоритмы на основе РСЛОС Комбинирующий генератор Фильтрующий генератор Генератор на основе композиции
- 15. Генераторы ИСП На основе шумящих диодов На
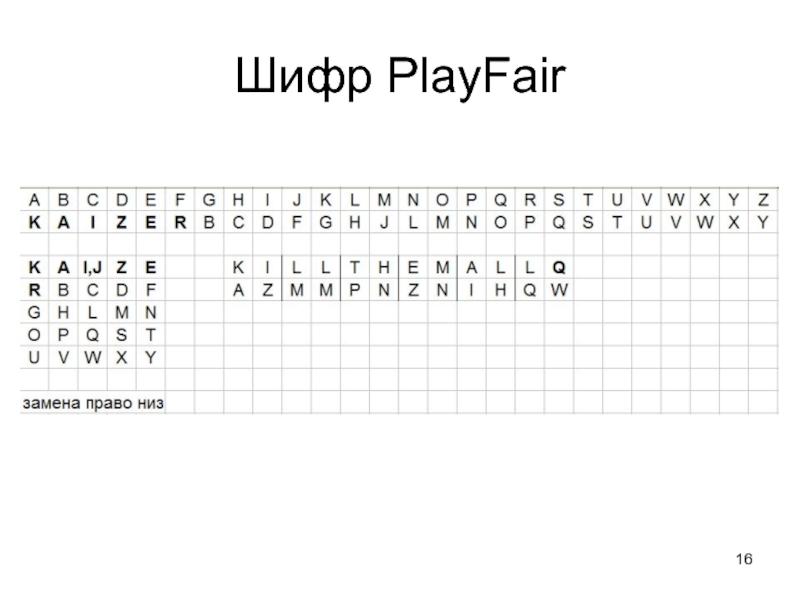
- 16. Шифр PlayFair
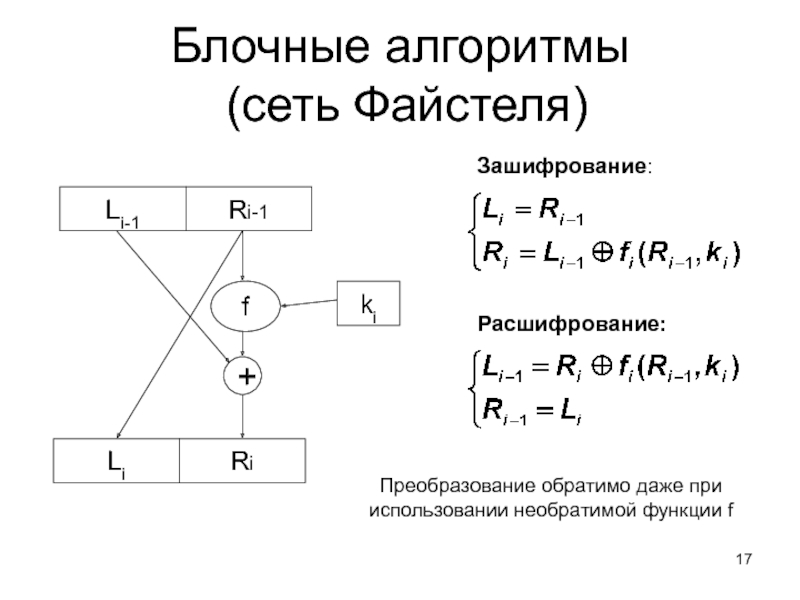
- 17. Блочные алгоритмы (сеть Файстеля) Li-1 Ri-1
- 18. Сравнительная характеристика блочных и поточных шифров
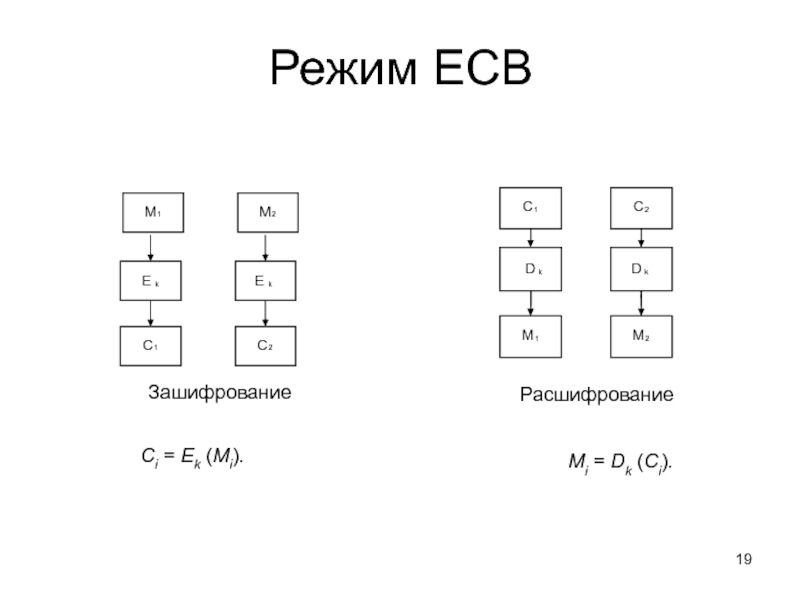
- 19. Режим ECB E k
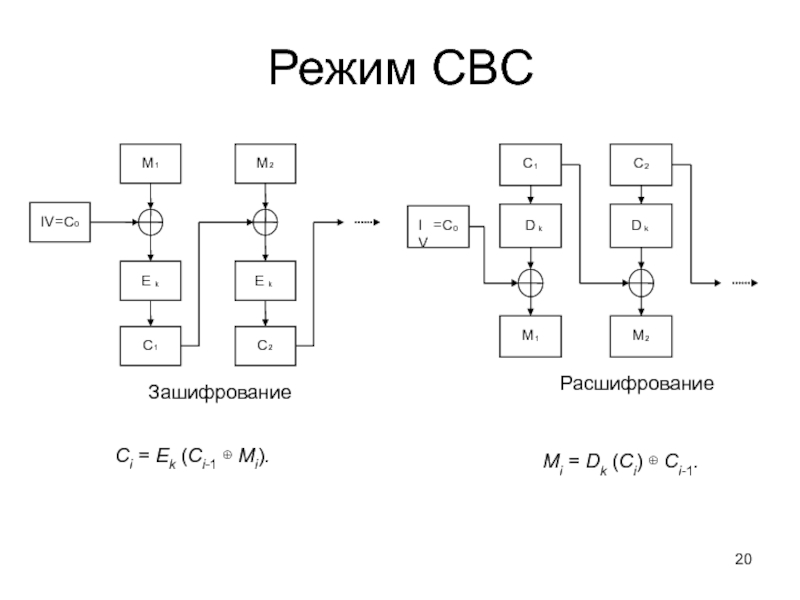
- 20. Режим CBC Сi = Ek (Ci-1 ⊕ Mi). Mi = Dk (Ci) ⊕ Ci-1.
- 21. Режим CFB
- 22. М 1
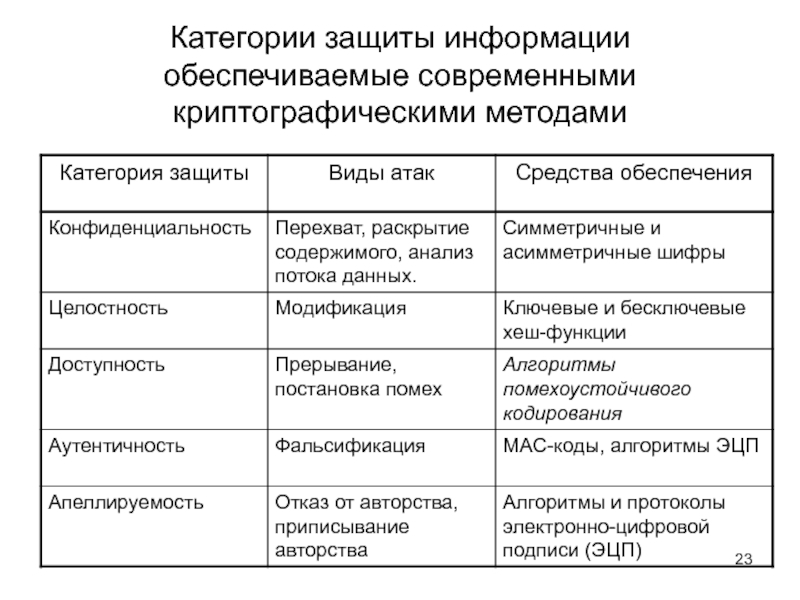
- 23. Категории защиты информации обеспечиваемые современными криптографическими методами
- 24. Порядок подготовки сообщения к передаче Имитовставка Помехоустойчивое кодирование Архивация Шифрование
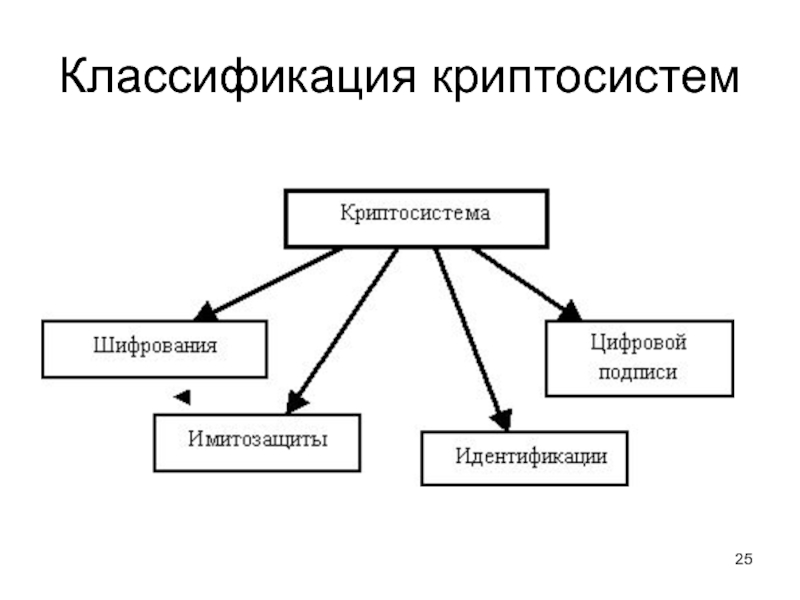
- 25. Классификация криптосистем
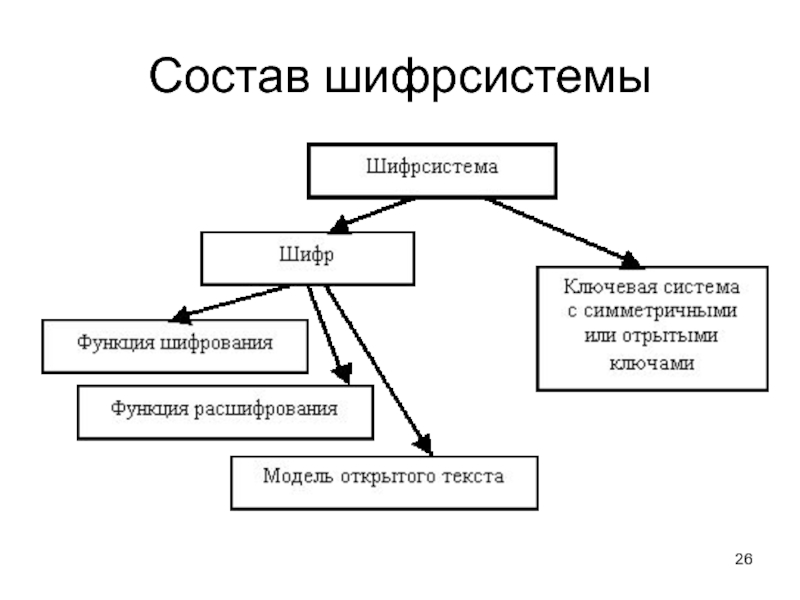
- 26. Состав шифрсистемы
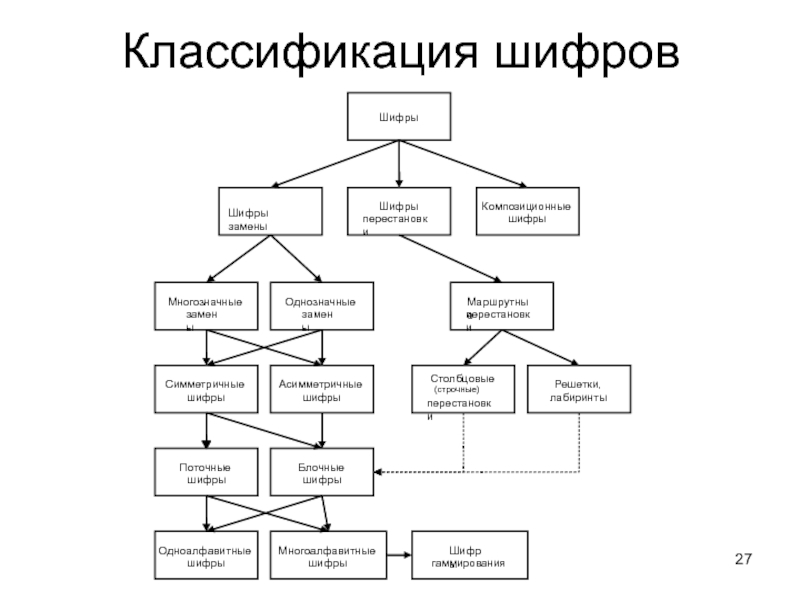
- 27. Классификация шифров
- 28. Схема симметричного шифрования Защищенный
- 29. Схема шифрования с открытым ключом Источник
- 30. Основные методы построения ассиметричных криптосистем Использование однонаправленных
- 31. Однонаправленная функция Функция f: U→V, обладающая двумя
- 32. Кандидаты на однонаправленную функцию Умножение натуральных чисел:
- 33. Однонаправленная функция с лазейкой (секретом) k Функция
- 34. Кандидат на однонаправленную функцию с секретом Модульное
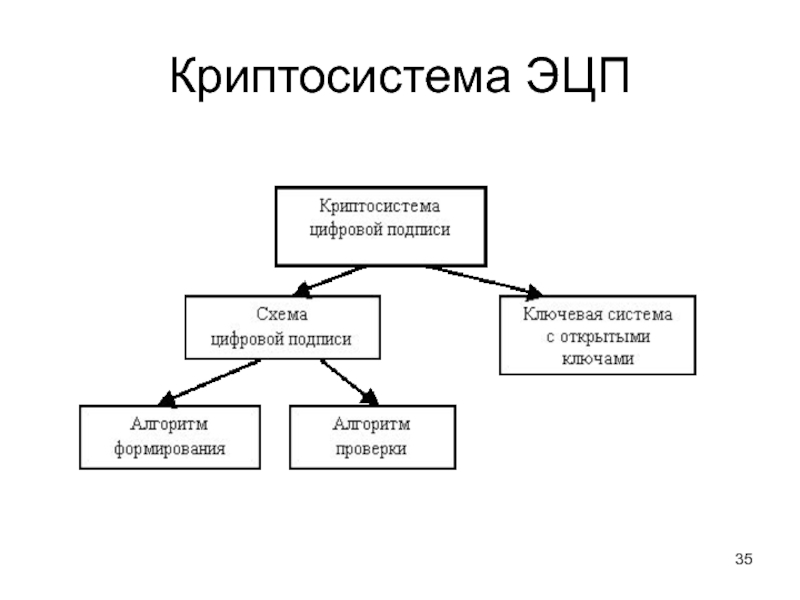
- 35. Криптосистема ЭЦП
- 36. Схема ЭЦП Источник сообщений Зашифрование Расшифрование
- 37. Сравнение электронной и собственноручной подписей
- 38. Криптографические хэш-функции Хэш-функцией называется всякая функция h:
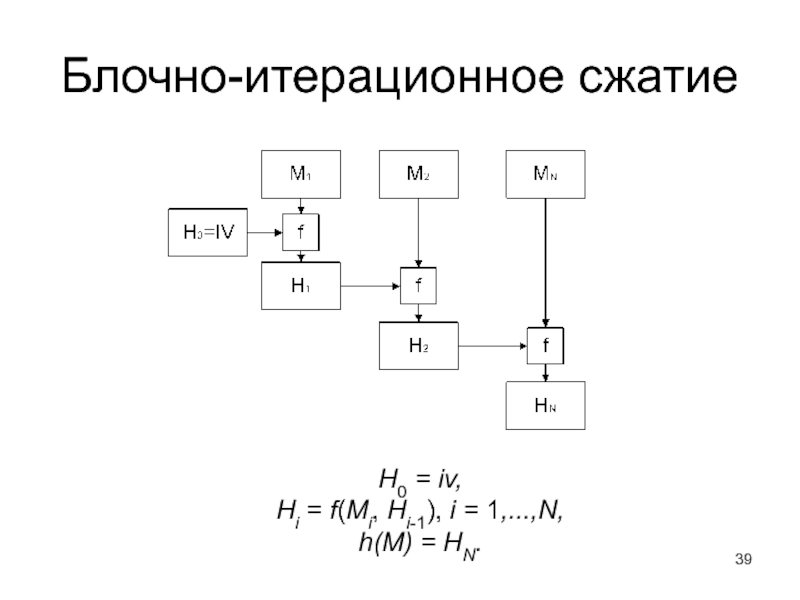
- 39. Блочно-итерационное сжатие H0 = iv, Hi = f(Мi, Hi-1), i = 1,...,N, h(M) = HN.
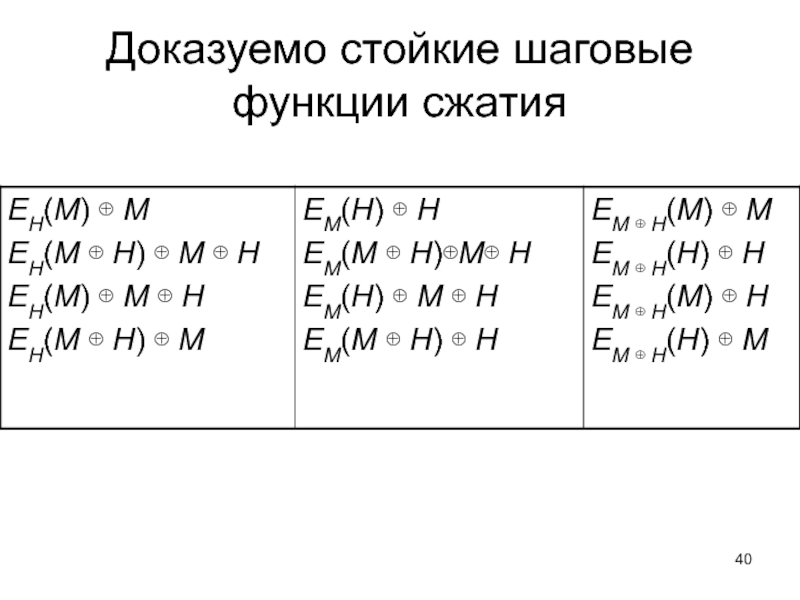
- 40. Доказуемо стойкие шаговые функции сжатия
- 41. Преобразование LPSX Ek(a) = L(P(S(X(k, a)))) где
- 42. Упрощенный пример 1001 0101 1110 0010
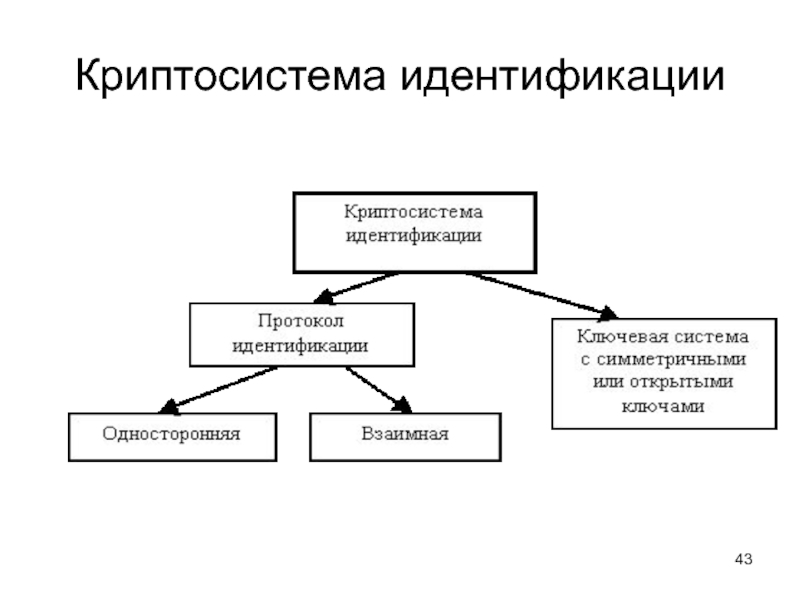
- 43. Криптосистема идентификации
- 44. Криптографические протоколы Виды криптографических протоколов: Протоколы с
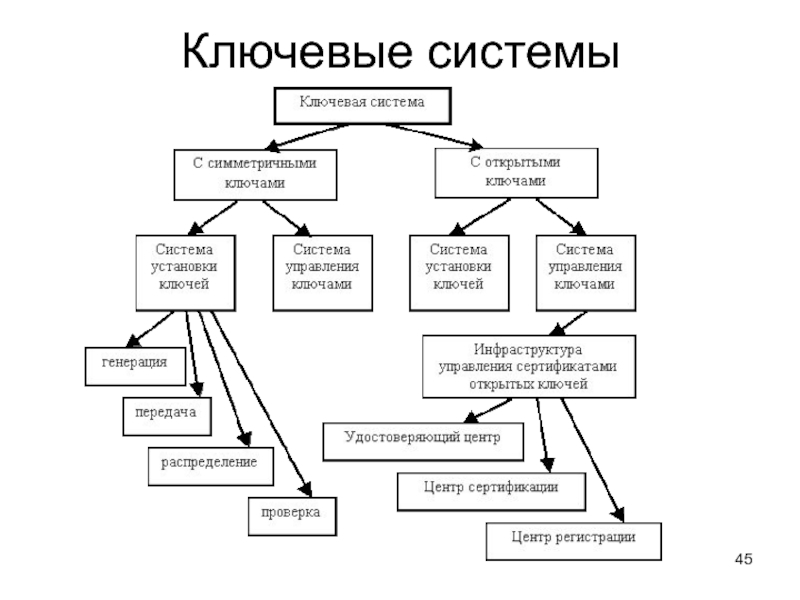
- 45. Ключевые системы
- 46. Отечественные криптографические стандарты ГОСТ 28147-89 (Алгоритм блочного шифрования)
- 47. Методы криптоанализа Статистические (исторические шифры) Дифференциальные (блочные
- 48. Перспективные направления в криптографии Вероятностное шифрование Основная
Исторически сложившиеся подходы к защите информации при ее передаче Физические методы (охрана, технические средства, нестандартные средства связи) защищенные каналы Стеганографические методы (сокрытие факта передачи информации) скрытые каналы Криптографические методы (использование шифров)
Слайд 1Криптографические методы защиты информации
История развития. Современное состояние. Перспективы.
Слайд 2Исторически сложившиеся подходы к защите информации при ее передаче
Физические методы (охрана,
технические средства, нестандартные средства связи) защищенные каналы
Стеганографические методы (сокрытие факта передачи информации) скрытые каналы
Криптографические методы (использование шифров) открытые каналы
Стеганографические методы (сокрытие факта передачи информации) скрытые каналы
Криптографические методы (использование шифров) открытые каналы
Слайд 3Различие между шифрованием и кодированием
Кодирование – жесткое правило замены одних символов
другими, предназначенное для удобства хранения и передачи информации
Шифрование – правило замены одних символов другими, предполагающее использование ключа, предназначенное для сокрытия смысла передаваемой и хранимой информациии
Шифрование – правило замены одних символов другими, предполагающее использование ключа, предназначенное для сокрытия смысла передаваемой и хранимой информациии
Слайд 4Правило Керкгоффса
«… компрометация системы не должна причинять неудобств корреспондентам…»
Жан-Вильгельм-Губерт-Виктор-Франсуа-Александр-Огюст Керкгоффс ван
Ньювенгоф
«Военная криптография». Конец 19 века.
«Военная криптография». Конец 19 века.
Стойкость (надежность) шифра определяется только секретностью ключа.
Слайд 5Постулаты разработки криптосистем
Противник может иметь в своем распоряжении:
Алгоритм
Шифратор
Образцы
шифрованных и открытых сообщений
и при этом не должен иметь возможности:
Восстановить применяемый ключ
Установить содержание остальных криптограмм
…располагая средствами, не превышающими стоимость защищаемой информации, за время в течение которого эта информация актуальна.
Слайд 6Методы криптографии
Криптографические алгоритмы:
Классическое шифрование
Поточные алгоритмы, криптографические генераторы
Блочные алгоритмы
Шифрсистемы с открытым ключом
RSA, шифрование на эллиптических кривых
Криптографические хэш-функции и пр.
Криптографические протоколы:
Аутентификация
Обмен ключами
Разделение секрета и пр.
Слайд 7Теория секретной связи
Клода Шеннона (1944 г.)
Концепция избыточности открытого текста и
переноса ее в шифртекст.
Теоретическая и практическая стойкость. Мера теоретической стойкости – энтропийная характеристика неопределенности шифра по открытому сообщению (расстояние единственности). Мера практической стойкости – рабочая характеристика шифра. (Временные затраты, количество операций, сложностные оценки вскрытия.)
Принцип рассеивания и перемешивания. Рассеивание – зависимость шифрованного текста от открытого текста и ключа должна быть сложной и неочевидной. Каждый элемент ключа и открытого текста должны влиять на каждый элемент шифрованного текста.
Теоретическая и практическая стойкость. Мера теоретической стойкости – энтропийная характеристика неопределенности шифра по открытому сообщению (расстояние единственности). Мера практической стойкости – рабочая характеристика шифра. (Временные затраты, количество операций, сложностные оценки вскрытия.)
Принцип рассеивания и перемешивания. Рассеивание – зависимость шифрованного текста от открытого текста и ключа должна быть сложной и неочевидной. Каждый элемент ключа и открытого текста должны влиять на каждый элемент шифрованного текста.
В России этими проблемами занимались А. А. Марков, Б. Б. Пиотровский, А. Н. Колмогоров. Множество их трудов до сих пор засекречено.
Слайд 8Математические модели шифров
Модель де Виари
для шифра Виженера:
Ci = E(mi) =
(mi + kj) mod 26
mi = D(Ci) = (Ci - kj) mod 26,
mi = D(Ci) = (Ci - kj) mod 26,
Модель де Виари
для шифра Бофора:
Ci = E(mi) = (kj - mi) mod 26
mi = D(Ci) = (kj - Ci) mod 26,
Модель шифра Вернама:
Ci = E(mi) = mi ⊕ kj
mi = D(Ci) = Ci ⊕ kj
Пусть:
i и j – номера шифрвеличины/шифробозначения и ключа
m, C и k – шифрвеличина, шифробозначение и ключ
E и D – операции шифрования и расшифрования
⊕ - операция XOR.
При j →∞ и равновероятном k
– имеем совершенный шифр
Дж. Моборна
Слайд 9Шифры Виженера и Бофора
(гаммирование таблицей Тритемия и модульное)
mi = ‘S’
(18)
kj = ‘Q’ (16)
по Виженеру:
Ci = 18 + 16 (mod 26) =
= 8 ( ‘I’ )
по Бофору:
Ci = 16 - 18 (mod 26) =
= 24 ( ‘Y’ )
по Виженеру:
mi = 8 - 16 (mod 26) =
= 18 ( ‘S’ )
по Бофору:
mi = 16 - 24 (mod 26) =
= 18 ( ‘S’ )
kj = ‘Q’ (16)
по Виженеру:
Ci = 18 + 16 (mod 26) =
= 8 ( ‘I’ )
по Бофору:
Ci = 16 - 18 (mod 26) =
= 24 ( ‘Y’ )
по Виженеру:
mi = 8 - 16 (mod 26) =
= 18 ( ‘S’ )
по Бофору:
mi = 16 - 24 (mod 26) =
= 18 ( ‘S’ )
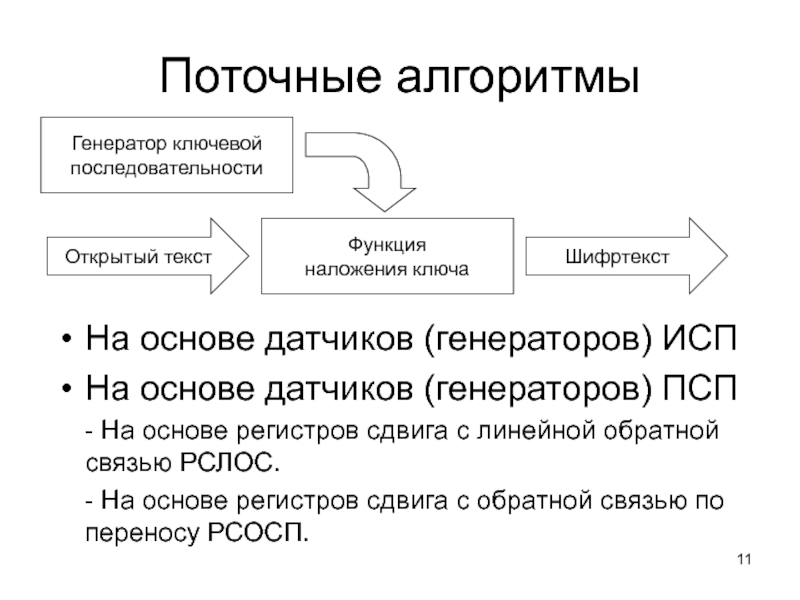
Слайд 11Поточные алгоритмы
На основе датчиков (генераторов) ИСП
На основе датчиков (генераторов) ПСП
- На основе регистров сдвига с линейной обратной связью РСЛОС.
- На основе регистров сдвига с обратной связью по переносу РСОСП.
- На основе регистров сдвига с обратной связью по переносу РСОСП.
Генератор ключевой
последовательности
Открытый текст
Функция
наложения ключа
Шифртекст
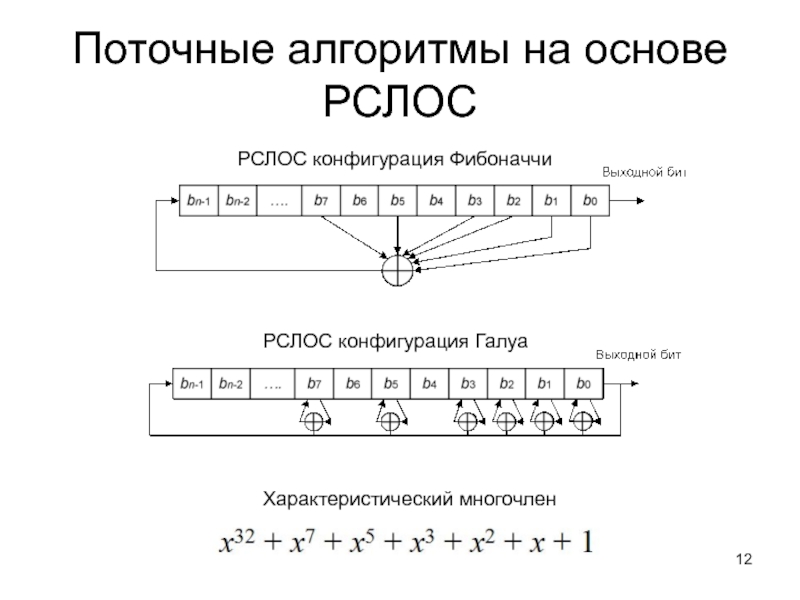
Слайд 12Поточные алгоритмы на основе РСЛОС
РСЛОС конфигурация Фибоначчи
РСЛОС конфигурация Галуа
Характеристический многочлен
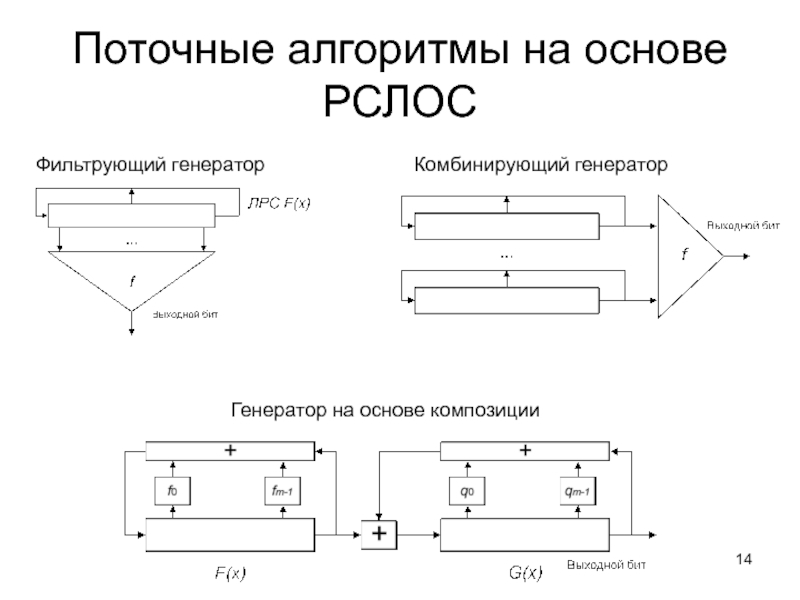
Слайд 14Поточные алгоритмы на основе РСЛОС
Комбинирующий генератор
Фильтрующий генератор
Генератор на основе композиции
Слайд 15Генераторы ИСП
На основе шумящих диодов
На основе счетчика Гейгера
Программные реализации по статистике
нажатия клавиш на клавиатуре.
На основе таймера компьютера
Таблицы случайных чисел
Основное назначение – генерация ключей и одноразовых блокнотов.
На основе таймера компьютера
Таблицы случайных чисел
Основное назначение – генерация ключей и одноразовых блокнотов.
Слайд 17Блочные алгоритмы
(сеть Файстеля)
Li-1
Ri-1
f
ki
+
Li
Ri
Зашифрование:
Расшифрование:
Преобразование обратимо даже при использовании необратимой функции f
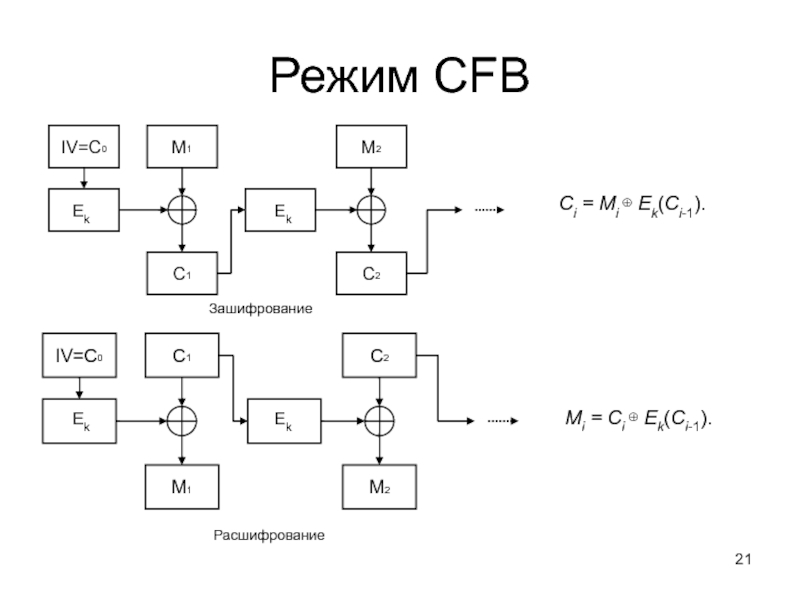
Слайд 21Режим CFB
М
1
Ek
C
1
IV
=
C
0
М
2
Ek
C
2
Зашифрование
Расшифрование
С
1
M
1
IV
=
C
0
C
2
M
2
Ek
Ek
Ci = Mi ⊕ Ek(Ci-1).
Mi = Ci ⊕ Ek(Ci-1).
Слайд 22
М
1
C
1
IV
=
Z
0
М
2
C
2
Зашифрование
Расшифрование
С
1
M
1
IV
=
Z
0
C
2
M
2
Ek
Ek
Ek
Ek
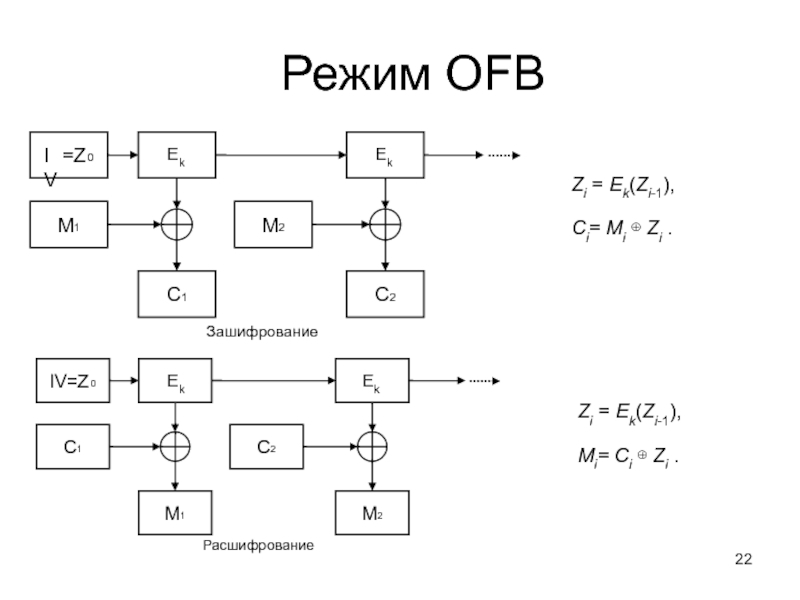
Zi = Ek(Zi-1),
Ci= Mi ⊕ Zi .
Zi = Ek(Zi-1),
Mi=
Ci ⊕ Zi .
Режим OFB
Слайд 24Порядок подготовки сообщения
к передаче
Имитовставка
Помехоустойчивое
кодирование
Архивация
Шифрование
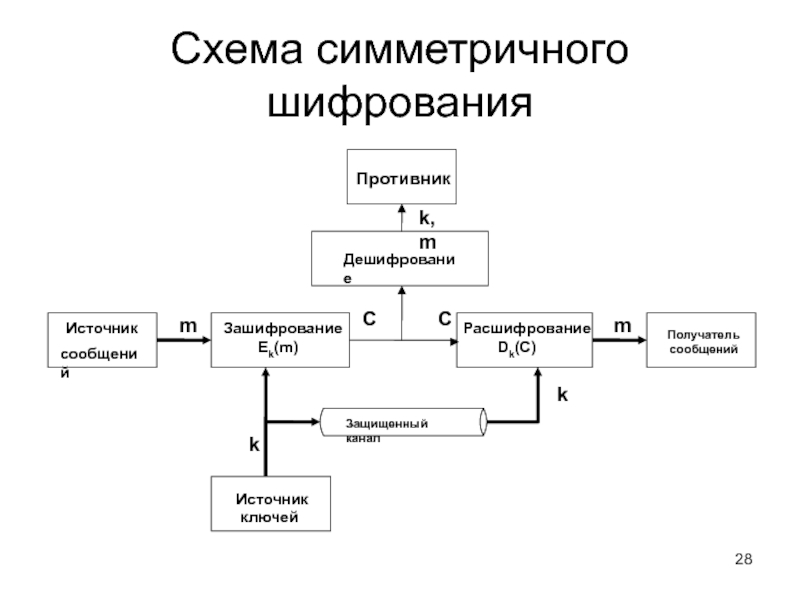
Слайд 28Схема симметричного шифрования
Защищенный канал
Зашифрование
Ek(m)
Источник
ключей
Расшифрование
Dk(C)
Источник
сообщений
Получатель
сообщений
Дешифрование
Противник
m
m
k
k
C
C
k, m
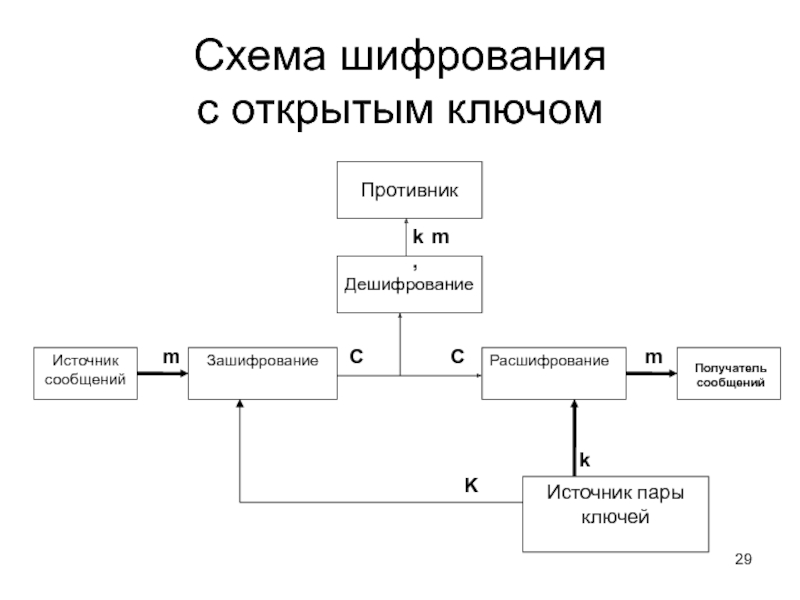
Слайд 29Схема шифрования
с открытым ключом
Источник
сообщений
Зашифрование
Расшифрование
Получатель
сообщений
Источник пары ключей
m
m
C
K
k
k,
m
Противник
Дешифрование
C
Слайд 30Основные методы построения ассиметричных криптосистем
Использование однонаправленных функций
Использование однонаправленных функций с секретом
Использование
маскировки вычислительно простых задач под вычислительно сложные
Использование кодов, исправляющих ошибки
Использование кодов, исправляющих ошибки
Слайд 31Однонаправленная функция
Функция f: U→V, обладающая двумя свойствами:
Для любого аргумента u ∈
U существует алгоритм вычисления значения f(u) полиномиальной сложности.
Не существует алгоритма инвертирования f (решения уравнения f(x) = v относительно x ∈ U), имеющего полиномиальную сложность.
Не существует алгоритма инвертирования f (решения уравнения f(x) = v относительно x ∈ U), имеющего полиномиальную сложность.
Слайд 32Кандидаты на однонаправленную функцию
Умножение натуральных чисел:
f(a,b) = a · b, a,b
∈N
Обратная задача: n = a · b (задача факторизации)
Модульное экспоненцирование с фиксированным основанием и модулем:
fa,n: Zn→Zn, где fa,n(m)=am mod n, a,m,n ∈Z
Обратная задача:ax = b mod n (задача дискретного логарифмирования)
3. Скалярное умножение точек эллиптической кривой над конечным полем.
Обратная задача: n = a · b (задача факторизации)
Модульное экспоненцирование с фиксированным основанием и модулем:
fa,n: Zn→Zn, где fa,n(m)=am mod n, a,m,n ∈Z
Обратная задача:ax = b mod n (задача дискретного логарифмирования)
3. Скалярное умножение точек эллиптической кривой над конечным полем.
Слайд 33Однонаправленная функция с лазейкой (секретом) k
Функция fk: U→V, обладающая двумя свойствами:
Для
любого аргумента u ∈ U существует алгоритм вычисления значения fk(u) полиномиальной сложности.
При неизвестном k не существует полиномиального алгоритма инвертирования fk.
При известном k существует полиномиальный алгоритм инвертирования fk.
При неизвестном k не существует полиномиального алгоритма инвертирования fk.
При известном k существует полиномиальный алгоритм инвертирования fk.
Слайд 34Кандидат на однонаправленную функцию с секретом
Модульное экспоненцирование с фиксированной степенью и
модулем:
ga,n: Zn→Zn, где ga,n(m)=am mod n, a,m,n ∈Z
Обратная задача:xm = b mod n (вычисление корня степени m по модулю n)
Секрет – разложение числа n.
Реализовано в системе RSA
ga,n: Zn→Zn, где ga,n(m)=am mod n, a,m,n ∈Z
Обратная задача:xm = b mod n (вычисление корня степени m по модулю n)
Секрет – разложение числа n.
Реализовано в системе RSA
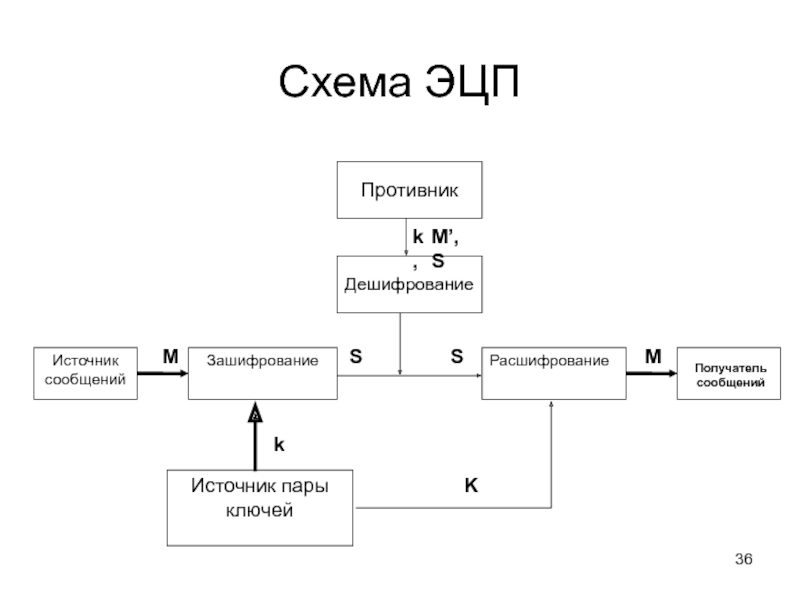
Слайд 36Схема ЭЦП
Источник
сообщений
Зашифрование
Расшифрование
Получатель
сообщений
Источник пары ключей
M
M
S
K
k
k,
M’,S
Противник
Дешифрование
S
Слайд 38Криптографические хэш-функции
Хэш-функцией называется всякая функция h: X → Y,
легко вычислимая
и такая, что для любого сообщения М
значение h(M) = Н (свертка) имеет фиксированную битовую длину.
значение h(M) = Н (свертка) имеет фиксированную битовую длину.
Ключевые Называются кодами аутентификации сообщений (КАС)
(message authentication code (MAC)).
Дают возможность без дополнительных средств гарантировать
как правильность источника данных, так и целостность данных
в системах с доверенной средой.
Применяются в системах с симметричными ключами.
Бесключевые. Называются кодами обнаружения ошибок
(modification detection code (MDC) или manipulation detection code,
message integrity code (MIC)).
Дают возможность с помощью дополнительных средств (например,
шифрования, использования защищенного канала или цифровой
подписи) гарантировать целостность данных.
Могут применяться в системах как с доверенной,
так и не доверенной средой.
Слайд 41Преобразование LPSX
Ek(a) = L(P(S(X(k, a))))
где
X = a ⊕ k
S – подстановка байтов
P – перестановка байтов
L – линейное преобразование подблоков
P – перестановка байтов
L – линейное преобразование подблоков
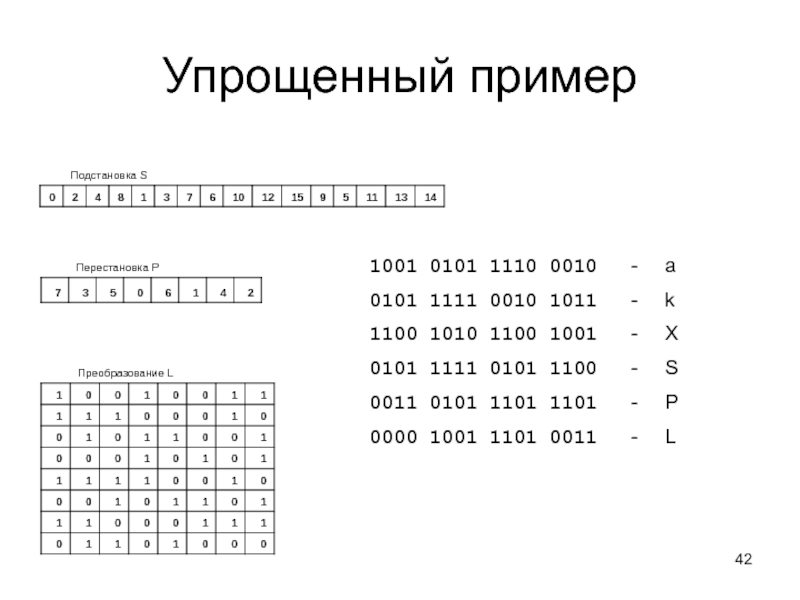
Слайд 42Упрощенный пример
1001 0101 1110 0010 - а
0101
1111 0010 1011 - k
1100 1010 1100 1001 - X
0101 1111 0101 1100 - S
0011 0101 1101 1101 - P
0000 1001 1101 0011 - L
1100 1010 1100 1001 - X
0101 1111 0101 1100 - S
0011 0101 1101 1101 - P
0000 1001 1101 0011 - L
Слайд 44Криптографические протоколы
Виды криптографических протоколов:
Протоколы с посредником
Протоколы с арбитром
Самодостаточные протоколы
Задачи, решаемые протоколами:
Основные
протоколы: Обмен ключами и распределение ключей,
аутентификация, разделение секрета.
Промежуточные протоколы: неоспоримые цифровые подписи,
метки времени, групповые подписи, подбрасывание монеты
по телефону, мысленный покер и пр.
Развитые протоколы: доказательства с нулевым разглашением,
одновременное подписание контракта, передача с забыванием,
одновременный обмен секретами, подписи вслепую и пр.
Эзотерические протоколы: тайное голосование, цифровые деньги,
тайные многосторонние вычисления и пр.
аутентификация, разделение секрета.
Промежуточные протоколы: неоспоримые цифровые подписи,
метки времени, групповые подписи, подбрасывание монеты
по телефону, мысленный покер и пр.
Развитые протоколы: доказательства с нулевым разглашением,
одновременное подписание контракта, передача с забыванием,
одновременный обмен секретами, подписи вслепую и пр.
Эзотерические протоколы: тайное голосование, цифровые деньги,
тайные многосторонние вычисления и пр.
Слайд 46Отечественные криптографические стандарты
ГОСТ 28147-89 (Алгоритм блочного шифрования)
ГОСТ Р 34.10-95, -2001, -2012 (Алгоритм цифровой
подписи на основе шифрования с открытым ключом)
ГОСТ Р 34.11-95, 2012 (Криптографическая хэш-функция)
ГОСТ Р 34.11-95, 2012 (Криптографическая хэш-функция)
Слайд 47Методы криптоанализа
Статистические (исторические шифры)
Дифференциальные (блочные шифры)
Бесключевого чтения (поточные шифры)
Линейные (блочные и
поточные шифры)
Вероятностные (шифрсистемы с открытым ключом)
Прямые (все виды шифров)
Вероятностные (шифрсистемы с открытым ключом)
Прямые (все виды шифров)
Слайд 48Перспективные направления в криптографии
Вероятностное шифрование
Основная цель – устранение утечки информации в
криптосистемах с открытым ключом
Квантовая криптография
Основная идея – создание канала связи, в котором невозможно прослушивание без нарушения в передаче (поляризованные фотоны)
Квантовая криптография
Основная идея – создание канала связи, в котором невозможно прослушивание без нарушения в передаче (поляризованные фотоны)
