Московский технологический институт
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Криптографическая защита информации презентация
Содержание
- 1. Криптографическая защита информации
- 2. Целью изучения дисциплины «Криптографическая защита информации»
- 3. Рекомендуемая литература
- 4. Криптографические методы защиты информации стали использоваться очень
- 5. Отправитель А и получатель В.
- 6. Перед тем как передать сообщение по
- 7. Можно описать шифр Цезаря в общем
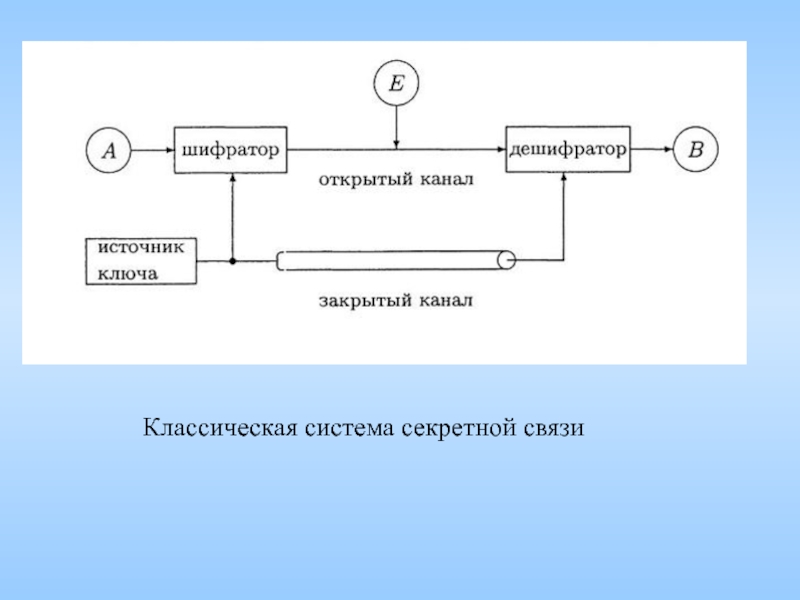
- 8. Классическая система секретной связи
- 9. Каждая попытка вскрытия шифра называется атакой
- 10. Объект Е перебирает последовательно все возможные
- 11. Объект А спрятал важные документы в
- 12. Расшифровка сообщения 26047 путем перебора ключей
- 13. В первом примере сообщение — текст
- 14. Описанная в приведенных примерах атака называется
- 15. Иногда считается, что более надежно использовать
- 16. Криптосистемы с открытым ключом Некоторые
- 17. Пусть дана функция определенная на
- 18. Значение данной функции вычисляется всего за 4 операции умножения.
- 19. Пример. Пусть требуется вычислить 3100 mod
- 20. Количество операций умножения при вычислении по
- 21. Покажем, что при больших р функция
- 22. Рассмотрим суперкомпьютер, который умножает два 90-значных
- 23. Криптосистемы с открытым ключом Некоторые
- 24. Хранение паролей в компьютере
- 25. Пароль при пересечении самолетом границы, запрашиваемый
- 26. Секретный пароль запрашиваемый в начале сеанса
Слайд 1Вебинар №1
Дисциплина: «Криптографическая защита информации»
Тема: «Основы защиты информации»
Преподаватель: Елисеев Владимир
Слайд 2 Целью изучения дисциплины «Криптографическая защита информации» является ознакомление с основными
Задачами дисциплины являются:
– рассмотреть основные шифры с открытыми ключами;
– изучить методы цифровой подписи;
– освоить основные криптографические протоколы, блоковые и потоковые шифры.
Слайд 4Криптографические методы защиты информации стали использоваться очень широко:
- межбанковские расчеты
- биржи, в которых все расчеты проводятся через Интернет
- расчеты по кредитным карточкам
- перевод заработной платы в банк
- заказ билетов через Интернет
- покупки в Интернет-магазинах и т.д.
Естественно, все эти операции, как и разговоры по мобильным телефонам и электронная почта, должны быть защищены от несанкционированного доступа.
Слайд 5Отправитель А и получатель В.
А и В абоненты некоторой сети,
Предполагается, что сообщения передаются по так называемому «открытому» каналу связи, в принципе доступному для прослушивания некоторым другим лицам, отличным от получателя и отправителя.
В криптографии обычно предполагается, что у лица, передающего сообщения и их принимающего, есть некоторый противник Е.
Слайд 6 Перед тем как передать сообщение по открытому каналу связи от
Шифр передается не по открытому каналу, а по специальному «закрытому» каналу, недоступному для прослушивания противником.
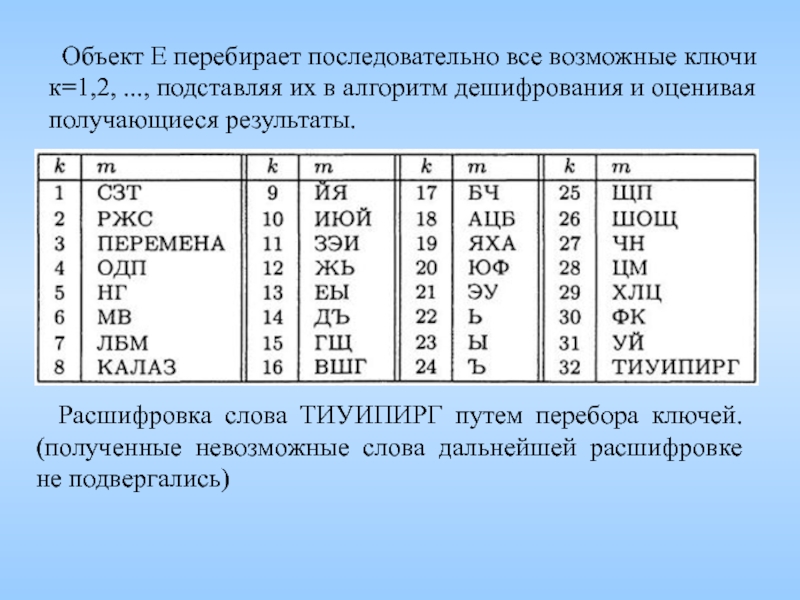
Шифр Гая Юлия Цезаря. Каждая буква сообщения заменяется на другую, номер которой в алфавите на три больше. Например, А заменяется на Г, Б на Д и т.д. Три последние буквы русского алфавита — Э, Ю, Я — шифруются буквами А, Б, В соответственно.
ПЕРЕМЕНА – (шифр Цезаря) – ТИУИПИРГ
Слайд 7 Можно описать шифр Цезаря в общем виде, если пронумеровать (закодировать)
Правило шифрования:
с = (m + к) mod 32
где m и с – номера букв соответственно сообщения и шифротекста, а к – некоторое целое число, называемое ключом шифра.
a mod b обозначает остаток от деления целого числа а на целое число b, причем остаток берется из множества {0,1,...,b-1}. Например, 13 mod 5 = 3.
Чтобы дешифровать зашифрованный текст, нужно применить «обратный» алгоритм
m = (с - к) mod 32.
Слайд 9 Каждая попытка вскрытия шифра называется атакой на шифр (или на
«Правило Керкхоффса»: противник может знать использованный алгоритм шифрования, характер передаваемых сообщений и перехваченный шифротекст, но не знает секретный ключ.
В нашем примере объект Е знает, что шифр был построен в соответствии с формулой алгоритма Цезаря, что исходное сообщение было на русском языке и что был передан шифротекст ТИУИПИРГ, но ключ объекту Е не известен.
Наиболее очевидная попытка расшифровки — последовательный перебор всех возможных ключей (так называемый метод «грубой силы» (brute-force attack)).
Слайд 10 Объект Е перебирает последовательно все возможные ключи к=1,2, ..., подставляя
Расшифровка слова ТИУИПИРГ путем перебора ключей. (полученные невозможные слова дальнейшей расшифровке не подвергались)
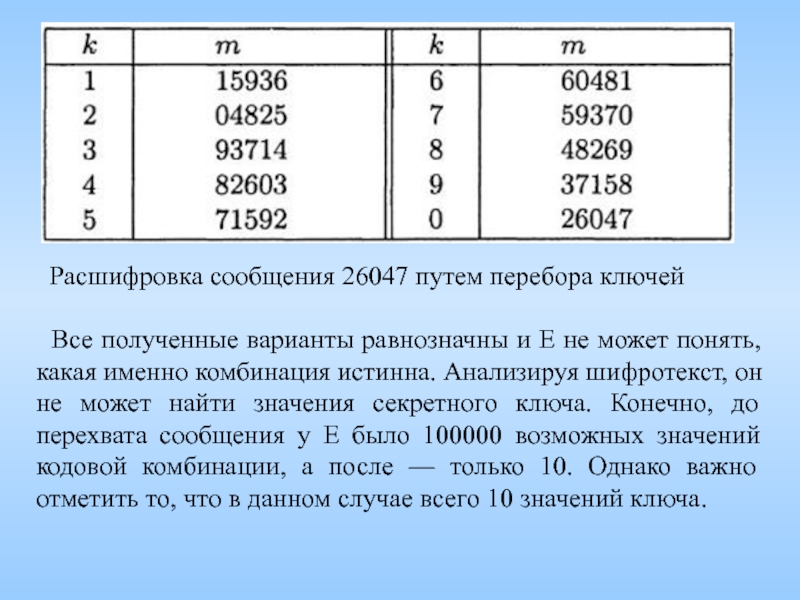
Слайд 11 Объект А спрятал важные документы в ячейке камеры хранения, снабженной
с = (m + к) mod 10.
Допустим, объект А послал объекту Б шифротекст 26047. Объект Е пытается расшифровать его, последовательно перебирая все возможные ключи.
Слайд 12 Расшифровка сообщения 26047 путем перебора ключей
Все полученные варианты равнозначны
Слайд 13 В первом примере сообщение — текст на русском языке, поэтому
Слайд 14 Описанная в приведенных примерах атака называется атакой по шифротексту.
Атака
Атаку по выбранному тексту, когда противник пользуется не только предоставленными ему парами «текст-шифротекст», но может и сам формировать нужные ему тексты и шифровать их с помощью того ключа, который он хочет узнать.
Слайд 15 Иногда считается, что более надежно использовать шифр, противостоящий атаке по
Возможно построение надежных криптосистем без защищенного канала. В таких системах А и Б вычисляют секретный ключ так, что Е не может этого сделать. Это открытие было сделано в основополагающих работах Диффи, Хеллмана и Меркля в 1976 году и открыло новую эру в современной криптографии.
Слайд 16 Криптосистемы с открытым ключом
Некоторые задачи криптографии:
- хранение паролей в компьютере;
секретный пароль запрашиваемый в начале сеанса банком у клиента.
Все эти проблемы решаются с использованием криптографических методов, основанных на понятии односторонней функции (one-way function).
Слайд 17 Пусть дана функция
определенная на конечном множестве X (х € X),
Функция называется односторонней, если вычисление по первой формуле — простая задача, требующая немного времени, а вычисление обратной функции — задача сложная, требующая привлечения массы вычислительных ресурсов
где р — некоторое простое число, а х — целое число из множества {1,2,...,р-1}. Обратная функция называется дискретным логарифмом
Слайд 19 Пример. Пусть требуется вычислить 3100 mod 7.
Имеем t =
Вычисляем числа ряда
а а2 а4 а8 а16 а32 а64 a=3
2 4 2 4 2 4 mod 7
100 = (1100100)2
Нам потребовалось всего 8 операций умножения
Слайд 20 Количество операций умножения при вычислении по описанному методу не превосходит
Столь же эффективные алгоритмы вычисления обратной функции неизвестны. Один из методов вычисления, называемый «шаг младенца, шаг великана». Этот метод требует порядка 2√р операций.
Слайд 21 Покажем, что при больших р функция действительно односторонняя, если для
Сколько десятичных знаков у чисел размером 512 бит, которые используются при данном алгоритме шифрования?
Слайд 22 Рассмотрим суперкомпьютер, который умножает два 90-значных числа за 10-14 сек.
Для вычисления прямой функции такому компьютеру потребуется Твыч.пр. = 600 • 10-14 = 6 • 10-12 сек.
А для вычисления обратной функции потребуется
Твыч.обр. = 1045 • 10-14 = 1031 сек., т.е. более 1022 лет.
Слайд 23 Криптосистемы с открытым ключом
Некоторые задачи криптографии:
- хранение паролей в компьютере;
секретный пароль запрашиваемый в начале сеанса банком у клиента.
Все эти проблемы решаются с использованием криптографических методов, основанных на понятии односторонней функции (one-way function).
Слайд 24 Хранение паролей в компьютере
Решение задачи основано на том, что
Слайд 25 Пароль при пересечении самолетом границы, запрашиваемый радиолокатором
Каждому «своему» самолету
СОКОЛ 05 02 01 12 45
(имя год месяц день часы минуты).
Полученное слово берётся за х, вычисляют у = ах mod p, где о и р не секретны. Затем самолет сообщает число у станции ПВО. Станция сравнивает вычисленное ею число у с полученным от самолета. Если вычисленное и полученное значения совпали, то самолет признается как «свой».















![Пример. Пусть требуется вычислить 3100 mod 7. Имеем t = [log100] = 6.(по основанию](/img/tmb/3/267790/488f06bbdbf3b82223630324fa9ebbba-800x.jpg)












