- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Компьютерное моделирование презентация
Содержание
- 1. Компьютерное моделирование
- 2. Особенности сложных систем как объекта моделирования
- 3. Понятие моделирование 1. Лучшее средство для
- 4. Моделирование – это во-первых, процесс создания
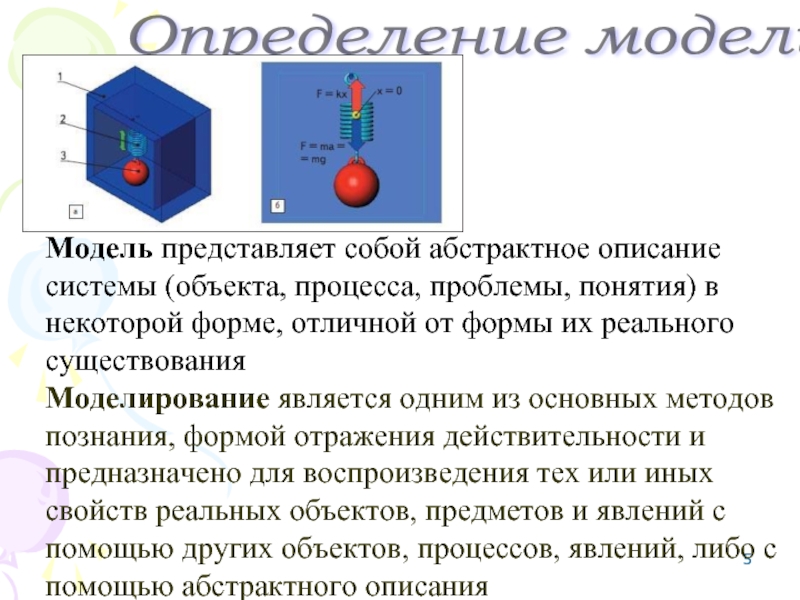
- 5. Определение модели Модель представляет собой абстрактное
- 6. Основные цели моделирования Прогноз - оценка
- 7. Классификация моделей Концептуальное моделирование – представление
- 8. Признаки классификации характер моделируемой стороны объекта; характер процессов, протекающих в объекте; способ реализации модели.
- 9. Классификация моделей по признаку "характер моделируемой стороны
- 10. Классификация моделей по признаку "характер процессов, протекающих
- 11. Классификация моделей и моделирования по признаку "способ
- 12. Абстрактные модели Абстрактные модели можно разделить
- 13. Математические модели Математические модели могут быть:
- 14. Компьютерное моделирование Компьютерное моделирование –
- 15. Компьютерное моделирование Суть компьютерного моделирования
- 16. Этапы моделирования Первый этап: уяснение целей
- 17. Адекватность модели Адекватность означает, достаточно ли
- 18. Адекватность модели Для оценки степени подобия
- 19. Требования, предъявляемые к моделям Модель должна
- 20. Внутренние свойства модели Модель должна быть:
Слайд 2Особенности сложных систем как объекта моделирования
Сложные системы, как правило, уникальны
Слабая
структурированность теоретических и фактических знаний о системе
Разнородность подсистем и элементов, составляющих систему
Случайность и неопределенность факторов, действующих в изучаемой системе
Многокритериальность оценок процессов, протекающих в системе
Разнородность подсистем и элементов, составляющих систему
Случайность и неопределенность факторов, действующих в изучаемой системе
Многокритериальность оценок процессов, протекающих в системе
Слайд 3Понятие моделирование
1. Лучшее средство для определения свойств объекта - натурный
эксперимент
2. Однако во многих случаях натурный эксперимент невозможен.
3. Выход из этого противоречия есть и называется он "моделирование
2. Однако во многих случаях натурный эксперимент невозможен.
3. Выход из этого противоречия есть и называется он "моделирование
Слайд 4 Моделирование – это
во-первых, процесс создания или отыскания в природе объекта,
который в некотором смысле может заменить исследуемый объект.
во-вторых, это испытание, исследование модели.
Модель является одновременно средством эксперимента и объектом эксперимента, заменяющим изучаемый объект
в-третьих, это перенос полученных на модели сведений на оригинал или, иначе, приписывание свойств модели оригиналу.
во-вторых, это испытание, исследование модели.
Модель является одновременно средством эксперимента и объектом эксперимента, заменяющим изучаемый объект
в-третьих, это перенос полученных на модели сведений на оригинал или, иначе, приписывание свойств модели оригиналу.
Понятие моделирование
Слайд 5Определение модели
Модель представляет собой абстрактное описание системы (объекта, процесса, проблемы,
понятия) в некоторой форме, отличной от формы их реального существования
Моделирование является одним из основных методов познания, формой отражения действительности и предназначено для воспроизведения тех или иных свойств реальных объектов, предметов и явлений с помощью других объектов, процессов, явлений, либо с помощью абстрактного описания
Моделирование является одним из основных методов познания, формой отражения действительности и предназначено для воспроизведения тех или иных свойств реальных объектов, предметов и явлений с помощью других объектов, процессов, явлений, либо с помощью абстрактного описания
Слайд 6Основные цели моделирования
Прогноз - оценка поведения системы при некотором сочетании ее
управляемых и неуправляемых параметров. Прогноз – главная цель моделирования.
Объяснение и лучшее понимание объектов. Здесь чаще других встречаются задачи оптимизации и анализа чувствительности.
Объяснение и лучшее понимание объектов. Здесь чаще других встречаются задачи оптимизации и анализа чувствительности.
Слайд 7Классификация моделей
Концептуальное моделирование – представление системы с помощью специальных знаков, символов,
операций над ними;
Физическое моделирование – моделируемый объект воспроизводится исходя из соотношения подобия, вытекающего из схожести физических явлений;
Структурно – функциональное моделирование – моделями являются схемы (блок-схемы), графики, и т.п.
Математическое (логико-математическое) моделирование – построение модели осуществляется средствами математики и логики
Физическое моделирование – моделируемый объект воспроизводится исходя из соотношения подобия, вытекающего из схожести физических явлений;
Структурно – функциональное моделирование – моделями являются схемы (блок-схемы), графики, и т.п.
Математическое (логико-математическое) моделирование – построение модели осуществляется средствами математики и логики
Слайд 8Признаки классификации
характер моделируемой стороны объекта;
характер процессов, протекающих в объекте;
способ реализации модели.
Слайд 9Классификация моделей по признаку "характер моделируемой стороны объекта"
функциональными (кибернетическими);
структурными;
Функциональные модели отображают
только поведение, функцию моделируемого объекта.
Структурное моделирование это создание и исследование модели, структура которой (элементы и связи) подобна структуре моделируемого объекта.
Структурное моделирование это создание и исследование модели, структура которой (элементы и связи) подобна структуре моделируемого объекта.
Слайд 10Классификация моделей по признаку "характер процессов, протекающих в объекте"
Детерминированные модели отображают
процессы, в которых отсутствуют случайные воздействия.
Стохастические модели отображают вероятностные процессы и события.
Статические модели служат для описания состояния объекта в какой-либо момент времени.
Динамические модели отображают поведение объекта во времени.
Дискретные модели отображают поведение систем с дискретными состояниями.
Непрерывные модели представляют системы с непрерывными процессами.
Дискретно-непрерывные модели строятся тогда, когда исследователя интересуют оба эти типа процессов.
Стохастические модели отображают вероятностные процессы и события.
Статические модели служат для описания состояния объекта в какой-либо момент времени.
Динамические модели отображают поведение объекта во времени.
Дискретные модели отображают поведение систем с дискретными состояниями.
Непрерывные модели представляют системы с непрерывными процессами.
Дискретно-непрерывные модели строятся тогда, когда исследователя интересуют оба эти типа процессов.
Слайд 11Классификация моделей и моделирования по признаку "способ реализации модели"
Абстрактные (мысленные)
модели;
Материальные модели.
Материальные модели представляют собой реальные технические конструкции.
Абстрактные модели представляют собой определенные конструкции из общепринятых знаков на бумаге или другом материальном носителе или в виде компьютерной программы.
Материальные модели.
Материальные модели представляют собой реальные технические конструкции.
Абстрактные модели представляют собой определенные конструкции из общепринятых знаков на бумаге или другом материальном носителе или в виде компьютерной программы.
Слайд 12Абстрактные модели
Абстрактные модели можно разделить на:
символические;
математические.
Символическая модель - это логический объект,
замещающий реальный процесс и выражающий основные свойства его отношений с помощью определенной системы знаков или символов.
Математическая модель— это «эквивалент» объекта, отражающий в математической форме важнейшие его свойства.
Математическая модель— это «эквивалент» объекта, отражающий в математической форме важнейшие его свойства.
Слайд 13Математические модели
Математические модели могут быть:
аналитическими;
имитационными;
смешанными (аналитико-имитационными)
Аналитические модели - это функциональные соотношения:
системы алгебраических, дифференциальных, интегро-дифференциальных уравнений, логических условий.
Имитационное моделирование предполагает представление модели в виде некоторого алгоритма, выполнение которого имитирует последовательность смены состояний в системе и таким образом представляет собой поведение моделируемой системы.
Имитационное моделирование предполагает представление модели в виде некоторого алгоритма, выполнение которого имитирует последовательность смены состояний в системе и таким образом представляет собой поведение моделируемой системы.
Слайд 14 Компьютерное моделирование
Компьютерное моделирование – метод решения задач анализа или синтеза
сложной системы на основе использования ее компьютерной модели.
Под термином “компьютерная модель”, чаще всего понимают:
Условный образ объекта, описанный с помощью взаимосвязанных компьютерных элементов (таблиц, блок-схем, диаграмм и т.д. ), отображающих структуру и взаимосвязи между элементами объекта
Отдельную программу, позволяющую с помощью последовательности вычислений и графического отображения их результатов, воспроизводить (имитировать) процессы функционирования объекта
Под термином “компьютерная модель”, чаще всего понимают:
Условный образ объекта, описанный с помощью взаимосвязанных компьютерных элементов (таблиц, блок-схем, диаграмм и т.д. ), отображающих структуру и взаимосвязи между элементами объекта
Отдельную программу, позволяющую с помощью последовательности вычислений и графического отображения их результатов, воспроизводить (имитировать) процессы функционирования объекта
Слайд 15 Компьютерное моделирование
Суть компьютерного моделирования заключена в получении количественных и качественных
результатов на имеющейся модели.
Методологией компьютерного моделирования является системный анализ
Методологией компьютерного моделирования является системный анализ
Слайд 16Этапы моделирования
Первый этап: уяснение целей моделирования
Второй этап: построение концептуальной модели
Третий этап:
выбор языка программирования или моделирования, разработка алгоритма и программы модели.
Четвертый этап: планирование эксперимента.
Пятый этап: выполнение эксперимента с моделью.
Шестой этап: обработка, анализ и интерпретация данных эксперимента.
Четвертый этап: планирование эксперимента.
Пятый этап: выполнение эксперимента с моделью.
Шестой этап: обработка, анализ и интерпретация данных эксперимента.
Слайд 17Адекватность модели
Адекватность означает, достаточно ли хорошо с точки зрения целей исследования
результаты, полученные в ходе моделирования, отражают истинное положение дел.
Предварительно исходный вариант математической модели подвергается следующим проверкам:
все ли существенные параметры включены в модель;
нет ли в модели несущественных параметров;
правильно ли отражены функциональные связи между параметрами;
правильно ли определены ограничения на значения параметров;
не дает ли модель абсурдные ответы, если ее параметры принимают предельные значения;
Предварительно исходный вариант математической модели подвергается следующим проверкам:
все ли существенные параметры включены в модель;
нет ли в модели несущественных параметров;
правильно ли отражены функциональные связи между параметрами;
правильно ли определены ограничения на значения параметров;
не дает ли модель абсурдные ответы, если ее параметры принимают предельные значения;
Слайд 18Адекватность модели
Для оценки степени подобия структур объектов (физических или математических) существует
понятие изоморфизма (изо - одинаковый, равный, морфе - форма, греч.).
Две системы изоморфны, если существует взаимно однозначное соответствие между элементами и отношениями (связями) этих систем.
Для оценки подобия в поведении (функционировании) систем существует понятие изофункционализма.
Две системы изофункциональны, если при одинаковых воздействиях они проявляют одинаковые реакции.
Две системы изоморфны, если существует взаимно однозначное соответствие между элементами и отношениями (связями) этих систем.
Для оценки подобия в поведении (функционировании) систем существует понятие изофункционализма.
Две системы изофункциональны, если при одинаковых воздействиях они проявляют одинаковые реакции.
Слайд 19Требования, предъявляемые к моделям
Модель должна быть актуальной
Модель должна быть результативной
Модель должна
быть дocтoвepнoй
Модель должна быть экономичной
Модель должна быть экономичной
Слайд 20Внутренние свойства модели
Модель должна быть:
Cyщecтвeннoй, т.е. пoзвoляющeй вcкpыть cyщнocть поведения системы,
вcкpыть неочевидные, нетривиальные детали.
Moщнoй, т.е. пoзвoляющeй пoлyчить шиpoкий набop существенных cвeдeний.
Пpocтoй в изyчeнии и иcпoльзoвaнии, лeгкo пpocчитывaeмoй на компьютере.
Открытой, т.е. позволяющей ее модификацию. В заключение темы сделаем несколько замечаний.
Moщнoй, т.е. пoзвoляющeй пoлyчить шиpoкий набop существенных cвeдeний.
Пpocтoй в изyчeнии и иcпoльзoвaнии, лeгкo пpocчитывaeмoй на компьютере.
Открытой, т.е. позволяющей ее модификацию. В заключение темы сделаем несколько замечаний.