- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Компьютерная графика и геометрическое моделирование презентация
Содержание
- 1. Компьютерная графика и геометрическое моделирование
- 2. Геометрическое моделирование Геометрическое моделирование как наука изучает
- 3. Моделирование и графика К компьютерному геометрическому моделированию
- 4. Разделы компьютерной графики технические средства машинной графики
- 5. интерактивная компьютерная графика (от английского Interaction —
- 6. Компьютерная графическая модель образ (изображение) материального объекта
- 7. Векторные графические модели Первой машиной, где ЭЛТ
- 8. Векторные графические модели состоят из последовательности непрерывных
- 9. Плоттеры
- 10. Рулонный каттер
- 11. + и – векторных устройств +
- 12. Компьютерная векторная геометрическая модель также составлена из
- 13. Преимущество векторной графики форма, пространственное положение и
- 14. Растеризация перед выводом на растровую технику производится
- 15. Растровые графические модели Растровые графические модели состоят
- 16. Растровые графические модели
- 17. Bitmap Компьютерное растровое изображение формируется построчно в
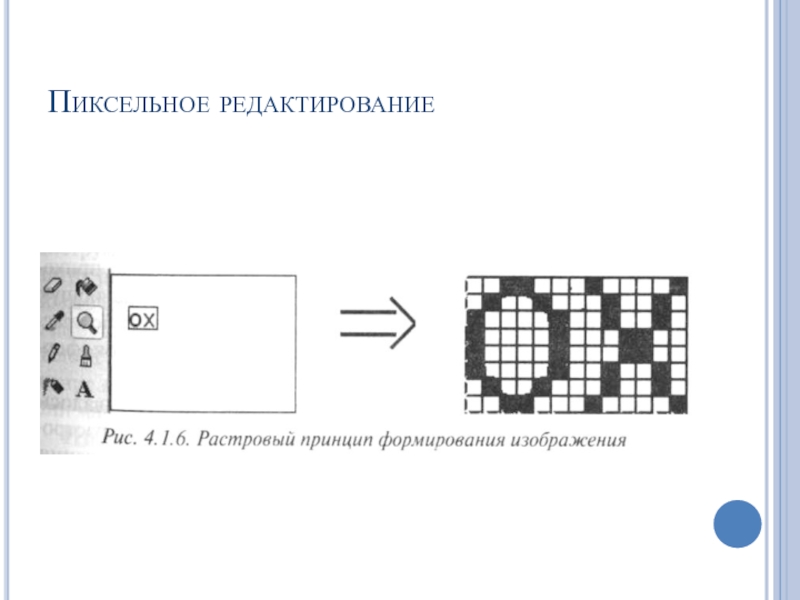
- 18. Пиксельное редактирование
- 19. Пиксели Растровые графические устройства: мониторы, сканеры, цифровые
- 20. Достоинства и недостатки растровой графики возможность закрашивания
- 21. Растровые устройства Наиболее популярными устройствами для получения
- 22. Растровый плоттер
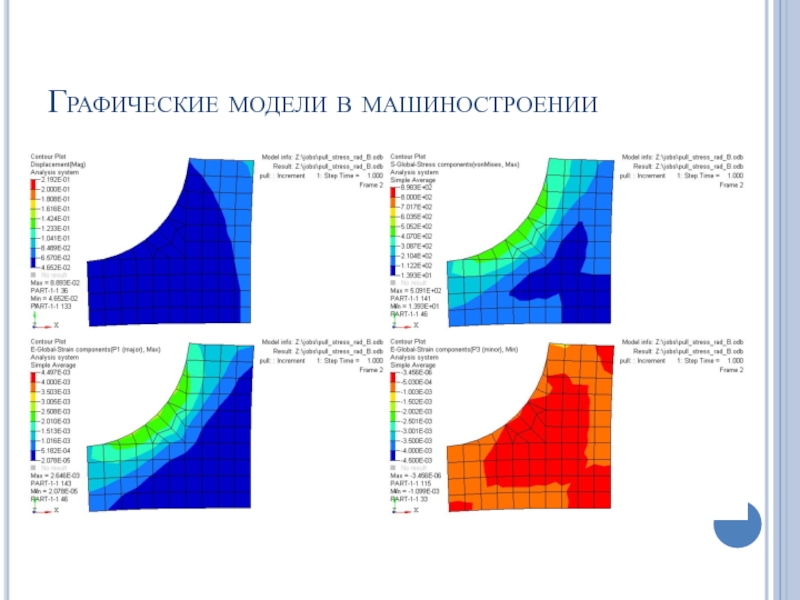
- 23. Графические модели в машиностроении
- 24. Графические модели в машиностроении
- 25. Векторизация графические модели могут быть модифицированы и
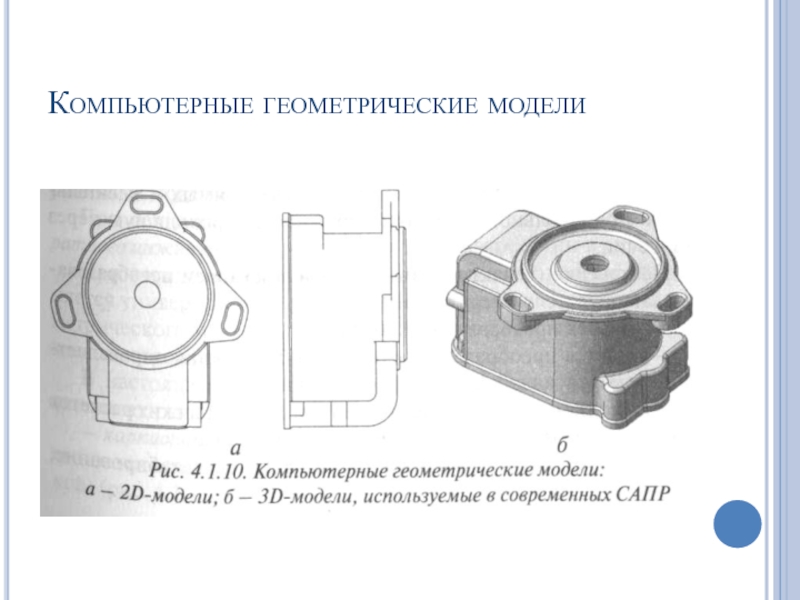
- 26. Компьютерные геометрические модели
- 27. 2D- модели Плоские компьютерные геометрические модели (2D-модели)
- 28. Способы построения 2D- модели Построение с использованием
- 29. Объемные (трехмерные) геометрические модели (ЗD-модели) Выделяют две
- 30. Типы ЗD-геометрических моделей каркасная ЗD-модель (wire frame
- 31. Базовые элементы (примитивы) изделий машиностроения — двумерные
- 32. Системы координат Характерные (базовые) точки геометрической модели
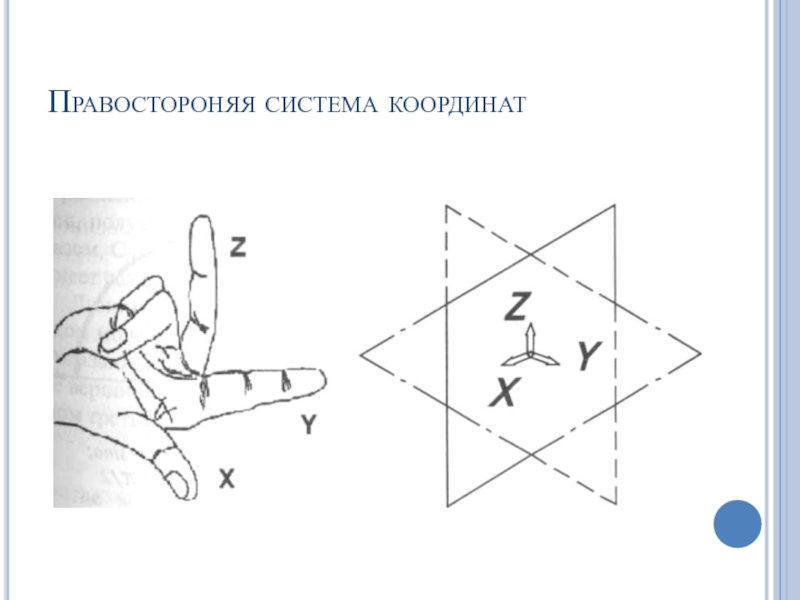
- 33. Правостороняя система координат
- 34. Моделирование линий
- 35. Кривые «Кривые» - общее название линий в
- 36. Параметрические и непараметрические кривые Явный вид: y=f(x)
- 37. Кривые
- 38. Трехмерные кривые Явная непараметрическая форма: Параметрическая форма:
- 39. Векторная параметрическая форма задания кривой Кривая в трехмерном пространстве: r=r(t)=[x(t), y(t), z(t)]
- 40. Уравнение прямой линии В явном виде: y=m*x+c В неявном виде: a*x+b*y+c=0
- 41. Уравнения кривых Уравнение явного вида: y=f(x) Подходит
- 42. Уравнения кривых Уравнение неявного вида: f(x, y)=0
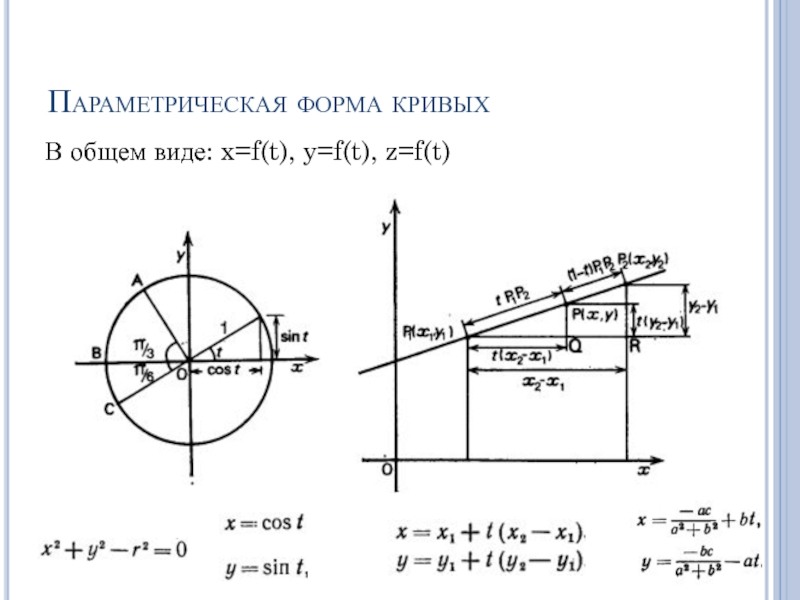
- 43. Параметрическая форма кривых В общем виде: x=f(t), y=f(t), z=f(t)
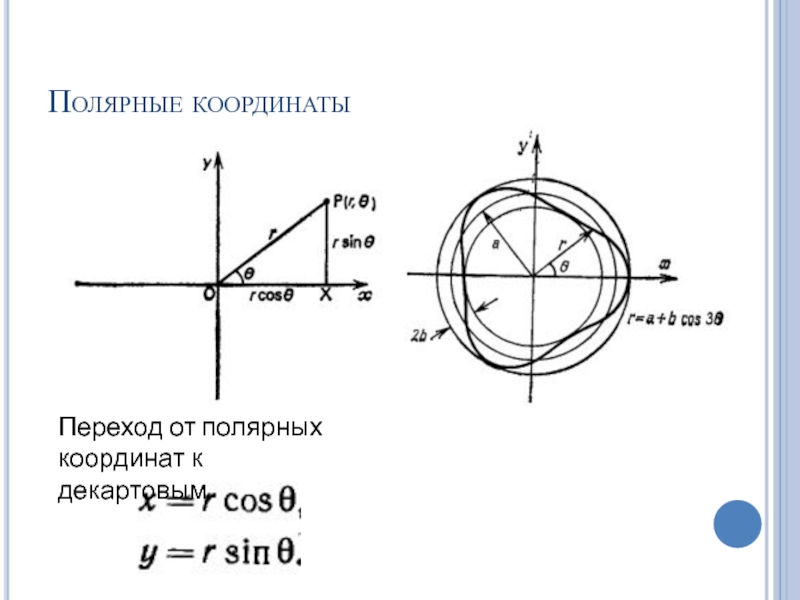
- 44. Полярные координаты Переход от полярных координат к декартовым
- 45. Произвольные кривые Линии для которых не известна
- 46. Сплайновые кривые Линии построенные по совокупности точек называют точечно-заданными Кубический сплайн (полином третьей степени)
- 47. Сплайновые кривые
- 48. Кривые Безье Кривая Безье – задается вершинами
- 49. Кривые Безье
- 50. Кривые NURBS Кривая NURBS –не проходит через
- 51. Кривые NURBS
- 52. Интерполяция и аппроксимация
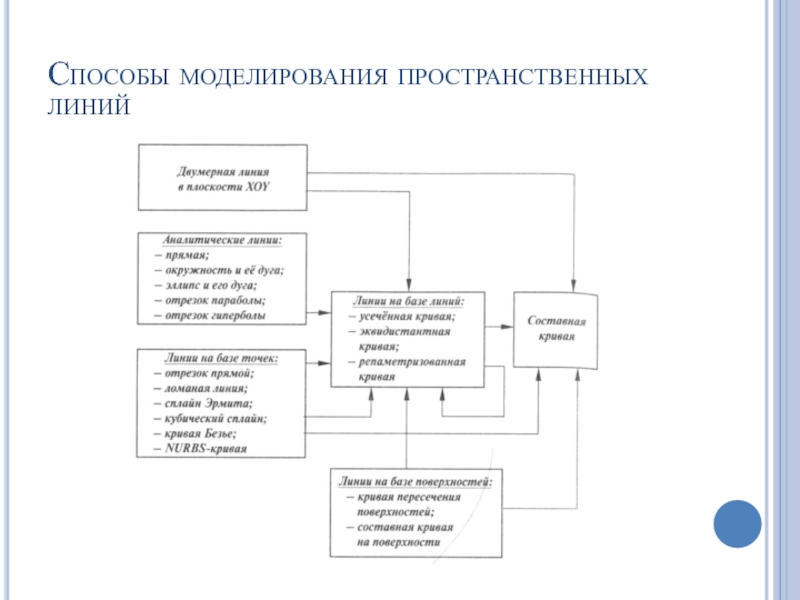
- 53. Способы моделирования пространственных линий
- 54. Построение поверхностей
- 55. Поверхность В общем случае математическая модель поверхности
- 56. Векторная параметрическая форма задания поверхности Поверхность в трехмерном пространстве: r=r(u, t)=[x(u, t), y(u, t), z(u,t)]
- 57. Способы задания поверхностей В явной форме:
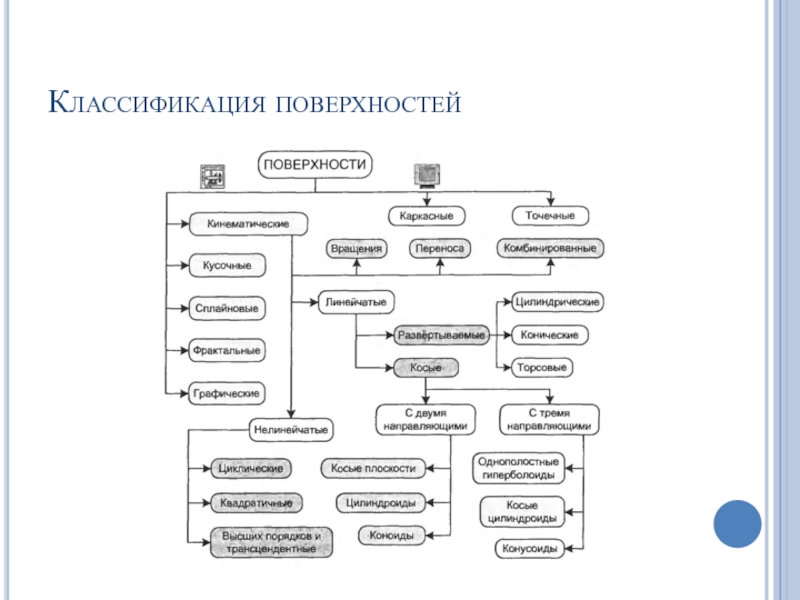
- 58. Классификация поверхностей
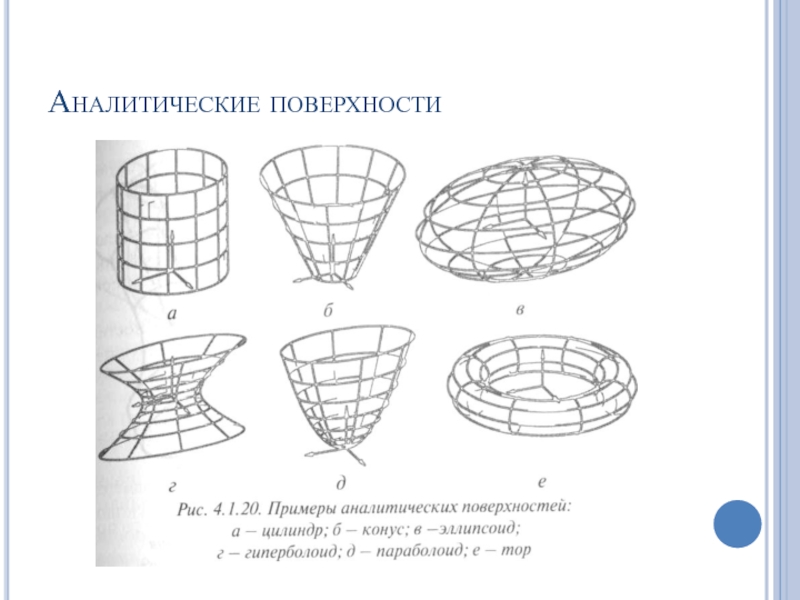
- 59. Аналитические поверхности Задаются параметрически, с помощью известный математических функций
- 60. Аналитические поверхности
- 61. Уравнение плоскости
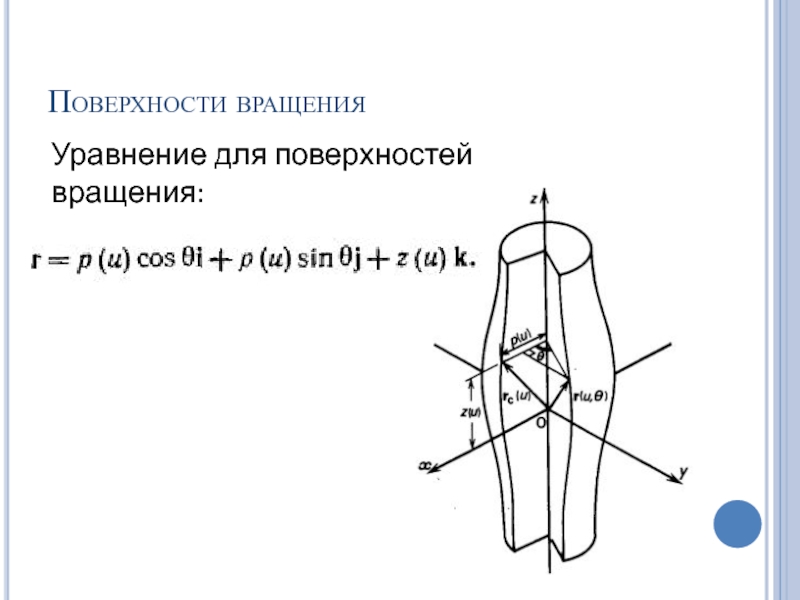
- 62. Поверхности вращения Уравнение для поверхностей вращения:
- 63. Эллипсоид вращения
- 64. Поверхности движения Получаются путем расчета движения кривой
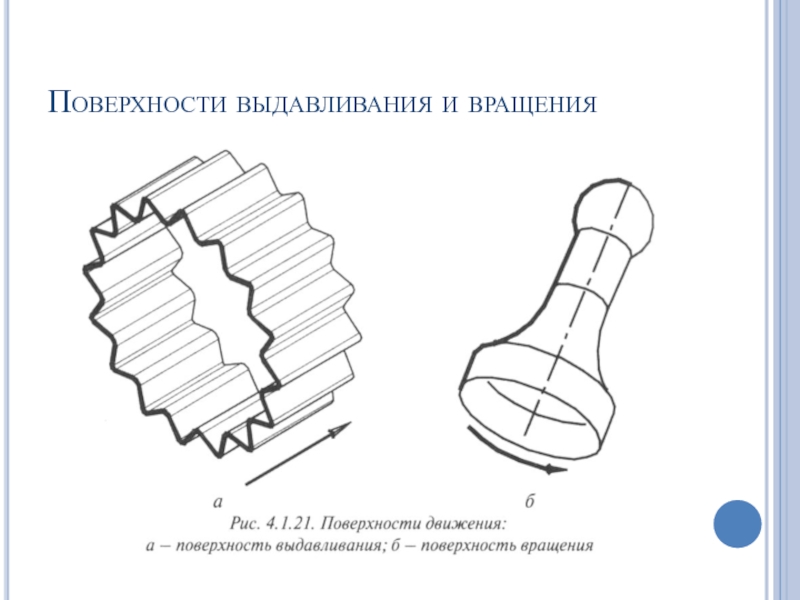
- 65. Поверхности выдавливания и вращения
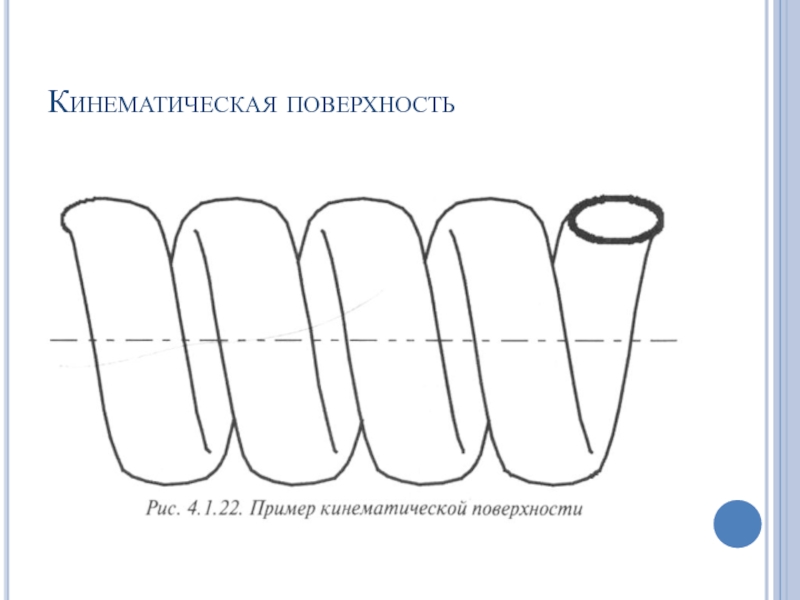
- 66. Кинематическая поверхность
- 67. Поверхности сдвига и заметания Образующая выполняет плоскопараллельное движение Образующая поворачивается с сохранением ориентации к направляющей
- 68. Линейчатая поверхность
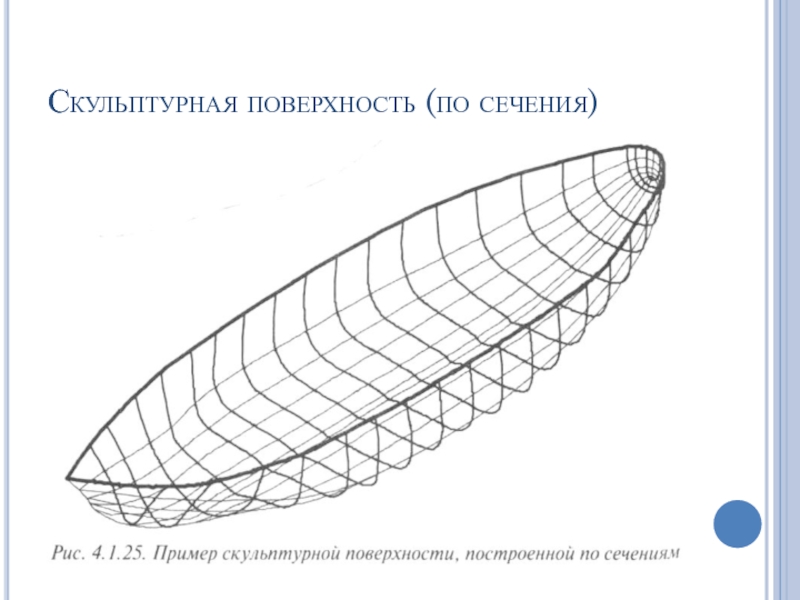
- 69. Скульптурная поверхность (по сечения)
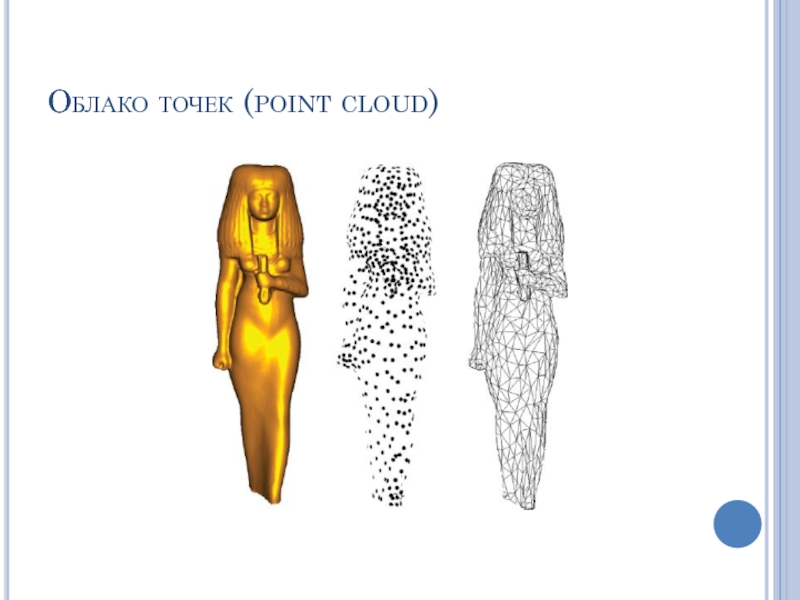
- 70. Облако точек (point cloud)
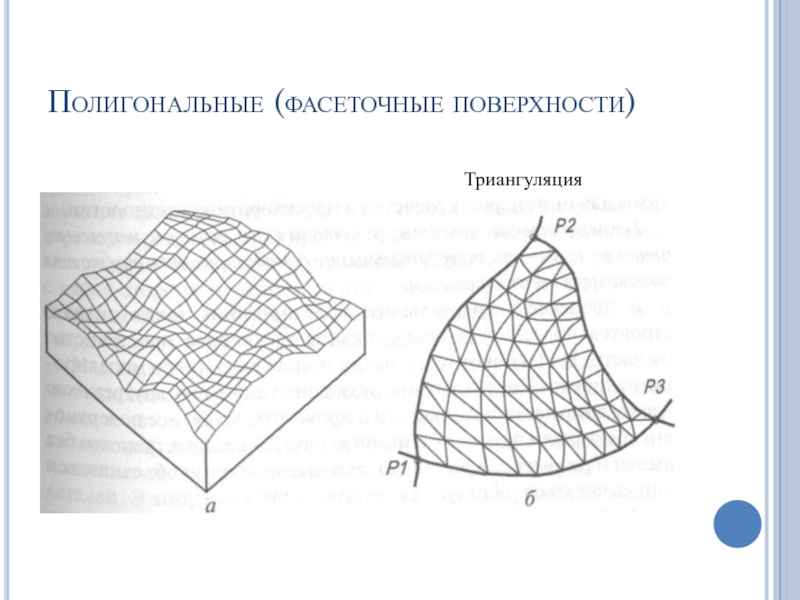
- 71. Полигональные (фасеточные поверхности) Триангуляция
- 72. Полигональные (фасеточные поверхности)
Геометрическое моделирование Геометрическое моделирование как наука изучает методы построения математических моделей, описывающих геометрические свойства предметов окружающего мира. Базируется на аналитической и дифференциальной геометрии, вычислительной математике, вариационном исчислении, топологии и разрабатывает
Слайд 2Геометрическое моделирование
Геометрическое моделирование как наука изучает методы построения математических моделей, описывающих
геометрические свойства предметов окружающего мира.
Базируется на аналитической и дифференциальной геометрии, вычислительной математике, вариационном исчислении, топологии и разрабатывает собственные математические методы моделирования
Базируется на аналитической и дифференциальной геометрии, вычислительной математике, вариационном исчислении, топологии и разрабатывает собственные математические методы моделирования
Слайд 3Моделирование и графика
К компьютерному геометрическому моделированию принято относить методы и алгоритмы
внутреннего представления и преобразования геометрических моделей (построение, редактирование и параметризацию) в ЭВМ.
Компьютерная графика занимается вопросами получения изображений тех же геометрических моделей с помощью технических средств ввода-вывода графической информации.
Компьютерная графика занимается вопросами получения изображений тех же геометрических моделей с помощью технических средств ввода-вывода графической информации.
Слайд 4Разделы компьютерной графики
технические средства машинной графики
методы визуализации и сканирования изображений
моделирование цвета,
текстуры, освещенности, прозрачности
алгоритмы построения и преобразования графических объектов (формирование геометрических примитивов, закраска областей, отсечение, выделение, проецирование, удаление скрытых линий и пр.).
алгоритмы построения и преобразования графических объектов (формирование геометрических примитивов, закраска областей, отсечение, выделение, проецирование, удаление скрытых линий и пр.).
Слайд 5интерактивная компьютерная графика
(от английского Interaction — взаимодействие),
создание геометрических моделей машиностроительных изделий
ведется в режиме человеко-машинного диалога с использованием графических окон и пиктограмм.
Слайд 6Компьютерная графическая модель
образ (изображение) материального объекта или математической модели, сформированный с
помощью компьютера и предназначенный для восприятия человеком.
К области действия компьютерной графики можно отнести все визуальные картины, получаемые с помощью компьютера, на экране монитора или твердом носителе (бумаге). Это, прежде всего, векторные и растровые рисунки, а также схемы, эскизы, чертежи и т.п.
К области действия компьютерной графики можно отнести все визуальные картины, получаемые с помощью компьютера, на экране монитора или твердом носителе (бумаге). Это, прежде всего, векторные и растровые рисунки, а также схемы, эскизы, чертежи и т.п.
Слайд 7Векторные графические модели
Первой машиной, где ЭЛТ использовалась в качестве устройства вывода,
была ЭВМ Whirlwind-I (Ураган-I), изготовленная в 1950 г. в Массачусетском технологическом институте.
С этого эксперимента начался этап развития векторных (каллиграфических) устройств и, соответственно, векторных графических моделей.
С этого эксперимента начался этап развития векторных (каллиграфических) устройств и, соответственно, векторных графических моделей.
Слайд 8Векторные графические модели
состоят из последовательности непрерывных линейных графических элементов (отрезки линий,
дуги, окружности, эллипсы и пр.).
На многих технических устройствах все линии, в том числе и кривые, формируются из множества коротких направленных отрезков — векторов.
В системах компьютерной графики векторные изображения могут быть получены исключительно при помощи специальных векторных устройств, таких как векторные дисплеи и перьевые плоттеры (от английского Plot — график, чертеж).
Плоттер = Графопостроитель
На многих технических устройствах все линии, в том числе и кривые, формируются из множества коротких направленных отрезков — векторов.
В системах компьютерной графики векторные изображения могут быть получены исключительно при помощи специальных векторных устройств, таких как векторные дисплеи и перьевые плоттеры (от английского Plot — график, чертеж).
Плоттер = Графопостроитель
Слайд 11+ и – векторных устройств
+ высокая точность и качество линий получаемого
изображения.
- медлительность
- высокая стоимость точных механических узлов
- медлительность
- высокая стоимость точных механических узлов
Слайд 12Компьютерная векторная геометрическая модель
также составлена из простейших линейных элементов (прямых, окружностей,
дуг, сплайнов и пр.) с известными формальными правилами их описания, но существует только во внутреннем (алгоритмическом) представлении компьютера.
Слайд 13Преимущество векторной графики
форма, пространственное положение и характеристики графических объектов описываются с
помощью аналитических формул.
Это обеспечивает:
небольшие размеры файлов
неограниченные возможности трансформации
независимость от принципа действия печатающего устройства или монитора.
Это обеспечивает:
небольшие размеры файлов
неограниченные возможности трансформации
независимость от принципа действия печатающего устройства или монитора.
Слайд 14Растеризация
перед выводом на растровую технику производится программное преобразование векторной модели в
растровую форму.
В состав Windows входит библиотека GDI (Graphics Device Interface) для осуществления вывода информации на графические периферийные устройства.
Существуют специальные PostScript-принтеры, имеющие встроенный аппаратный растеризатор (RIP — Raster Image Proceccor), который оперативно преобразует векторные данные, подготовленные на специальном графическом языке векторного моделирования PostScript в растровую форму.
В состав Windows входит библиотека GDI (Graphics Device Interface) для осуществления вывода информации на графические периферийные устройства.
Существуют специальные PostScript-принтеры, имеющие встроенный аппаратный растеризатор (RIP — Raster Image Proceccor), который оперативно преобразует векторные данные, подготовленные на специальном графическом языке векторного моделирования PostScript в растровую форму.
Слайд 15Растровые графические модели
Растровые графические модели состоят из регулярно расположенных точек, называемых
пикселями (pixels — от английского picture element — элемент изображения)
Слайд 17Bitmap
Компьютерное растровое изображение формируется построчно в виде прямоугольной матрицы, каждая ячейка
которой представляет собой небольшую закрашенную площадку. Такая матрица получила название битовой карты (bitmap)
Битовая карта кодируется как набор (массив) троек чисел: две координаты пикселя на плоскости и его цвет. Это внутреннее представление можно считать растровой геометрической компьютерной моделью, состоящей только из точек, которая при выводе на техническое устройство отображается на соответствующее множество (матрицу) графических элементов монитора или принтера
Битовая карта кодируется как набор (массив) троек чисел: две координаты пикселя на плоскости и его цвет. Это внутреннее представление можно считать растровой геометрической компьютерной моделью, состоящей только из точек, которая при выводе на техническое устройство отображается на соответствующее множество (матрицу) графических элементов монитора или принтера
Слайд 19Пиксели
Растровые графические устройства: мониторы, сканеры, цифровые фото- и видеокамеры, принтеры.
Размеры
пикселя стараются выбрать минимально возможными, но при масштабировании растровой картины эти площадки могут стать очень заметными
Слайд 20Достоинства и недостатки растровой графики
возможность закрашивания (заливки) всей площади изображения, что
позволяет формировать «фотореалистические» картины.
Алгоритмы обработки растровых моделей отличаются простотой и высокой скоростью.
Пиксели не привязаны к физическим элементам устройств, поэтому легко можно управлять точностью растровой модели, назначая более грубое или тонкое разбиение.
относительно низкая точность изображения. При использовании устройств с небольшим разрешением, это может быть очень заметно.
При подробном разбиении изображения на множество пикселей резко возрастает объем необходимой для хранения растровой модели памяти.
Алгоритмы обработки растровых моделей отличаются простотой и высокой скоростью.
Пиксели не привязаны к физическим элементам устройств, поэтому легко можно управлять точностью растровой модели, назначая более грубое или тонкое разбиение.
относительно низкая точность изображения. При использовании устройств с небольшим разрешением, это может быть очень заметно.
При подробном разбиении изображения на множество пикселей резко возрастает объем необходимой для хранения растровой модели памяти.
Слайд 21Растровые устройства
Наиболее популярными устройствами для получения широкоформатных изображений в промышленности (например,
чертежей в САПР) являются струйные плоттеры (Ink-Jet Plotter).
Качество растровых устройств вывода графических изображений принято измерять в «Dpi» (dots per inch — число точек на дюйм)
Качество сканирования целесообразно измерять в «Lpi» (Lines per inch - число линий на дюйм).
Качество растровых устройств вывода графических изображений принято измерять в «Dpi» (dots per inch — число точек на дюйм)
Качество сканирования целесообразно измерять в «Lpi» (Lines per inch - число линий на дюйм).
Слайд 25Векторизация
графические модели могут быть модифицированы и видоизменены только в очень ограниченных
пределах, налагаемых используемым способом представления.
Для превращения графического изображения в необходимую для практической работы геометрическую модель обязательно требуется так называемая «векторизация» — компьютерная обработка и преобразование растрового изображения в векторное представление (векторную геометрическую модель).
Она может быть выполнена с точностью, не превышающей точность отсканированного оригинала, поэтому ценность для САПР отсканированных чертежей, даже после самой лучшей векторизации, не слишком велика.
Для превращения графического изображения в необходимую для практической работы геометрическую модель обязательно требуется так называемая «векторизация» — компьютерная обработка и преобразование растрового изображения в векторное представление (векторную геометрическую модель).
Она может быть выполнена с точностью, не превышающей точность отсканированного оригинала, поэтому ценность для САПР отсканированных чертежей, даже после самой лучшей векторизации, не слишком велика.
Слайд 272D- модели
Плоские компьютерные геометрические модели (2D-модели) используются в подсистемах САПР, предназначенных
для разработки конструкторской документации — 2D-CAD- системы
Слайд 28Способы построения 2D- модели
Построение с использованием отношений заключается в том, что
последовательно пользователем задаются:
примитив, подлежащий построению;
список отношений и примитивы, к которым заданы отношения.
Построение (редактирование) с использованием преобразований заключается в следующем:
задается преобразуемый объект;
задается преобразование (вид преобразования определяется соответствующей функцией — командой);
выполнение преобразования путем аналитических расчетов и операций с векторной математической моделью. Например, сдвиг, копирование, поворот, масштабирование, отсечение и т.д.
примитив, подлежащий построению;
список отношений и примитивы, к которым заданы отношения.
Построение (редактирование) с использованием преобразований заключается в следующем:
задается преобразуемый объект;
задается преобразование (вид преобразования определяется соответствующей функцией — командой);
выполнение преобразования путем аналитических расчетов и операций с векторной математической моделью. Например, сдвиг, копирование, поворот, масштабирование, отсечение и т.д.
Слайд 29Объемные (трехмерные) геометрические модели (ЗD-модели)
Выделяют две основные инженерные задачи, связанные с
компьютерным моделированием трехмерных тел в машиностроении:
построение компьютерной модели уже существующего изделия или его материальной модели (технологии «обратного инжиниринга»);
синтез формы ранее не существовавшего (даже в виде материальных моделей) проектируемого изделия (универсальное программное обеспечение подсистем геометрического моделирования).
построение компьютерной модели уже существующего изделия или его материальной модели (технологии «обратного инжиниринга»);
синтез формы ранее не существовавшего (даже в виде материальных моделей) проектируемого изделия (универсальное программное обеспечение подсистем геометрического моделирования).
Слайд 30Типы ЗD-геометрических моделей
каркасная ЗD-модель (wire frame model)
поверхностная ЗD-модель (surface model)
твердотельная модель
ЗD-модель (solid model)
Слайд 31Базовые элементы (примитивы) изделий машиностроения
— двумерные объекты (точки, прямые, отрезки прямых,
окружности и их дуги, различные плоские кривые и контуры);
— поверхности (плоскости, поверхности, представленные семейством образующих, поверхности движения, криволинейные поверхности);
объемные примитивы (параллелепипеды, призмы, пирамиды, конусы, произвольные многогранники).
— поверхности (плоскости, поверхности, представленные семейством образующих, поверхности движения, криволинейные поверхности);
объемные примитивы (параллелепипеды, призмы, пирамиды, конусы, произвольные многогранники).
Слайд 32Системы координат
Характерные (базовые) точки геометрической модели задают координатами в декартовой системе
относительно выбранного начала координат.
Так называемая «мировая» (глобальная, исходная) система координат (МСК— в англоязычных версиях — WCS), дающая начало отсчета, задается автоматически в программе моделирования. Относительно этой системы конструктор может задать произвольное количество дополнительных «пользовательских » (локальная) систем координат (ПСК— (ICS).
Так называемая «мировая» (глобальная, исходная) система координат (МСК— в англоязычных версиях — WCS), дающая начало отсчета, задается автоматически в программе моделирования. Относительно этой системы конструктор может задать произвольное количество дополнительных «пользовательских » (локальная) систем координат (ПСК— (ICS).
Слайд 35Кривые
«Кривые» - общее название линий в геометрическом моделировании.
Элементарные кривые задаются аналитически
Кривая
может быть представлена в параметрической и непараметрической форме
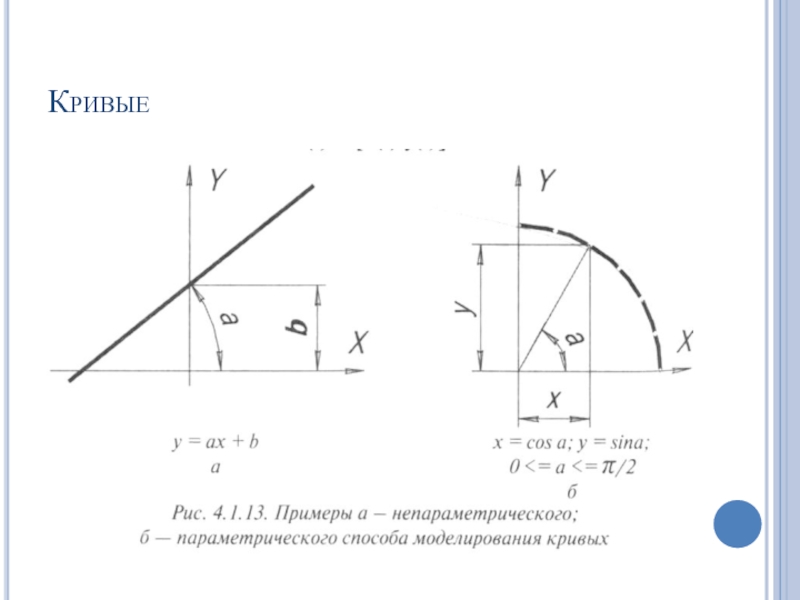
Слайд 36Параметрические и непараметрические кривые
Явный вид:
y=f(x)
Неявный вид:
F(x,y)=0
Параметрический вид:
x=x(t)
y=y(t)
Векторное представление
точки на кривой:
P(t)=[x(t) y(t)]
P(t)=[x(t) y(t)]
Слайд 39Векторная параметрическая форма задания кривой
Кривая в трехмерном пространстве:
r=r(t)=[x(t), y(t), z(t)]
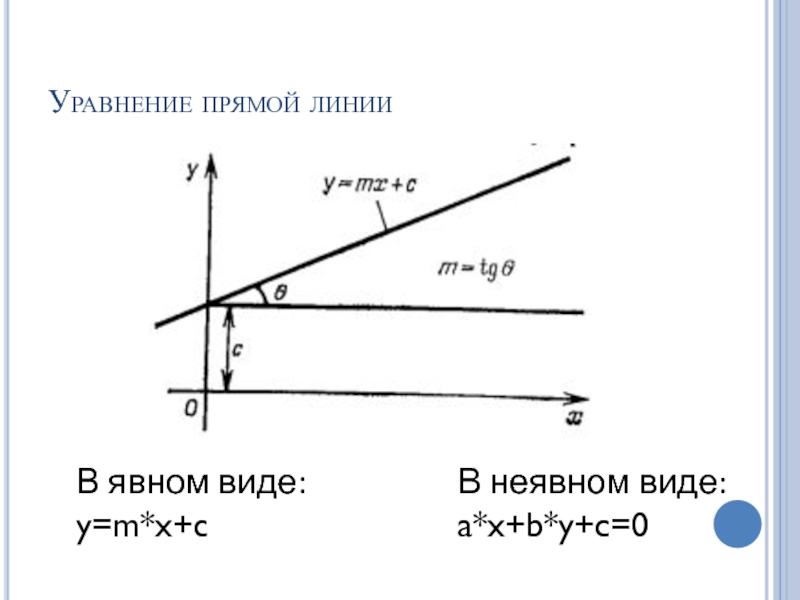
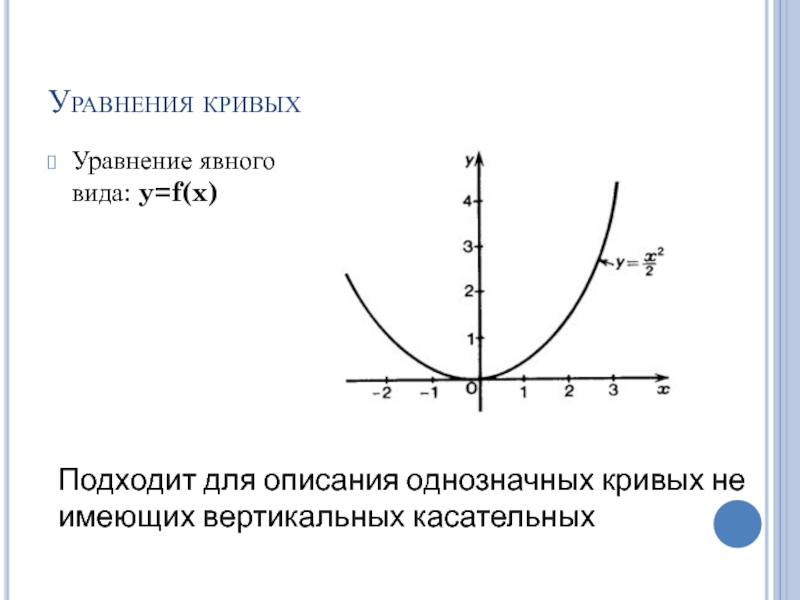
Слайд 41Уравнения кривых
Уравнение явного вида: y=f(x)
Подходит для описания однозначных кривых не имеющих
вертикальных касательных
Слайд 42Уравнения кривых
Уравнение неявного вида: f(x, y)=0
Позволяет установить находится ли точка на
кривой, но не удобно для практического вычисления точек на кривой
Слайд 45Произвольные кривые
Линии для которых не известна аналитическая формула задаются с помощью
сплайнов
Сплайн – параметрическая кривая, задаваемая последовательностью точек
Сплайн – параметрическая кривая, задаваемая последовательностью точек
Слайд 46Сплайновые кривые
Линии построенные по совокупности точек называют точечно-заданными
Кубический сплайн (полином третьей
степени)
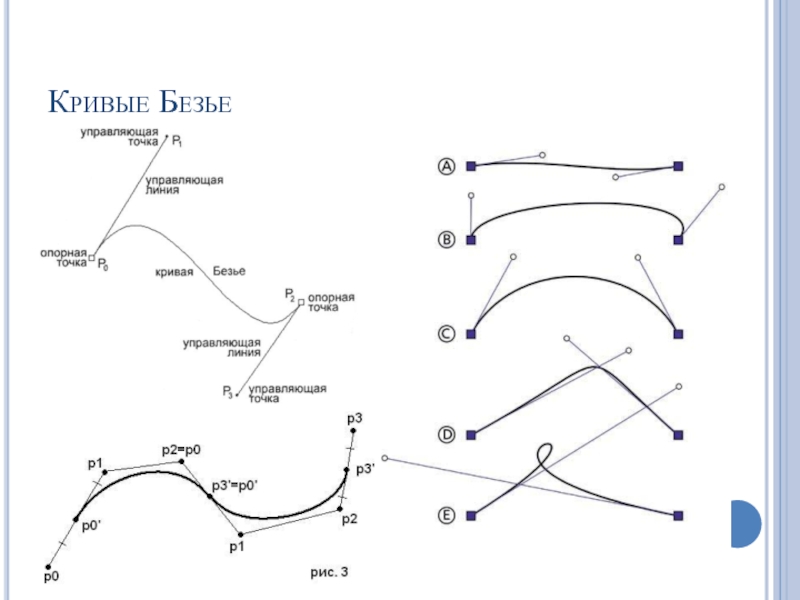
Слайд 48Кривые Безье
Кривая Безье – задается вершинами многоугольника и в общем случае
не проходит через базовые точки
Для получения кривой проходящей через заданные точки используют составные кривые Безье
Такие кривые можно использовать для целей интерполяции
Для получения кривой проходящей через заданные точки используют составные кривые Безье
Такие кривые можно использовать для целей интерполяции
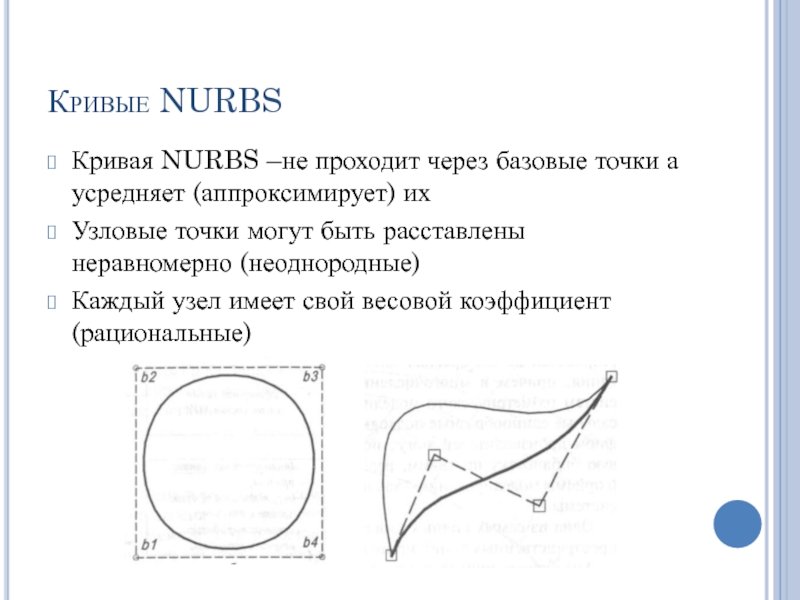
Слайд 50Кривые NURBS
Кривая NURBS –не проходит через базовые точки а усредняет (аппроксимирует)
их
Узловые точки могут быть расставлены неравномерно (неоднородные)
Каждый узел имеет свой весовой коэффициент (рациональные)
Узловые точки могут быть расставлены неравномерно (неоднородные)
Каждый узел имеет свой весовой коэффициент (рациональные)
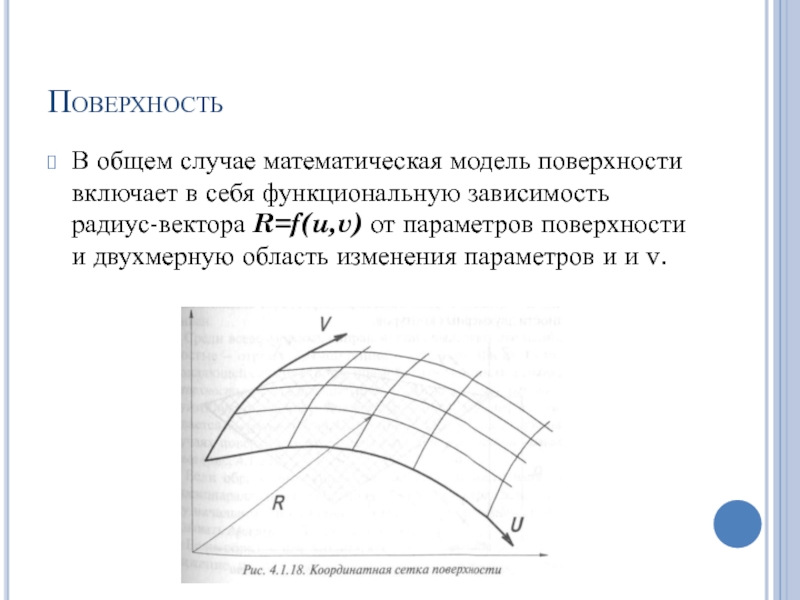
Слайд 55Поверхность
В общем случае математическая модель поверхности включает в себя функциональную зависимость
радиус-вектора R=f(u,v) от параметров поверхности и двухмерную область изменения параметров и и v.
Слайд 56Векторная параметрическая форма задания поверхности
Поверхность в трехмерном пространстве:
r=r(u, t)=[x(u, t), y(u,
t), z(u,t)]
Слайд 57Способы задания поверхностей
В явной форме: z=F(x, y)
В неявной форме: F(x, y,
z) = 0
В параметрической форме: x=f(u, v)
y=f(u, v)
z=f(u, v)
В параметрической форме: x=f(u, v)
y=f(u, v)
z=f(u, v)
Слайд 59Аналитические поверхности
Задаются параметрически, с помощью известный математических функций
Слайд 64Поверхности движения
Получаются путем расчета движения кривой по заданной траектории
Образующая – перемещающаяся
кривая
Направляющая – траектория движения
Направляющая отрезок – поверхность выдавливания
Направляющая дуга или окружность – поверхность вращения
Остальные случаи – кинематическая поверхность
Направляющая – траектория движения
Направляющая отрезок – поверхность выдавливания
Направляющая дуга или окружность – поверхность вращения
Остальные случаи – кинематическая поверхность
Слайд 67Поверхности сдвига и заметания
Образующая выполняет плоскопараллельное движение
Образующая поворачивается с сохранением ориентации
к направляющей
