- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Комплексная безопасность информационных систем. Асимметричные алгоритмы шифрования. (Лекция 8) презентация
Содержание
- 1. Комплексная безопасность информационных систем. Асимметричные алгоритмы шифрования. (Лекция 8)
- 2. УЧЕБНЫЕ ВОПРОСЫ 1
- 3. ЛИТЕРАТУРА 2 1. А.А. ВАРФОЛОМЕЕВ ОСНОВЫ
- 4. 3 1. ОБОБЩЕННАЯ СХЕМА АСИММЕТРИЧНЫХ АЛГОРИТМОВ ШИФРОВАНИЯ
- 5. 3 1. ОБОБЩЕННАЯ СХЕМА АСИММЕТРИЧНЫХ АЛГОРИТМОВ ШИФРОВАНИЯ
- 6. 3 1. ОБОБЩЕННАЯ СХЕМА АСИММЕТРИЧНЫХ АЛГОРИТМОВ ШИФРОВАНИЯ
- 7. 3 1. ОБОБЩЕННАЯ СХЕМА АСИММЕТРИЧНЫХ АЛГОРИТМОВ ШИФРОВАНИЯ
- 8. 3 1. АЛГОРИТМ ДИФФИ — ХЕЛЛМАНА
- 9. 3 1. КРИПТОСИСТЕМА RSA Криптоалгоритм RSA
- 10. 3 1. КРИПТОСИСТЕМА RSA ПРИМЕР
- 11. 2. СХЕМА ЭЛЬ-ГАМАЛЯ Схема Эль-Гамаля (Elgamal) — криптосистема (Elgamal) — криптосистема с
- 12. 2. СХЕМА ЭЛЬ-ГАМАЛЯ Работа в режиме шифрования
- 13. 2. СХЕМА ЭЛЬ-ГАМАЛЯ
- 14. 2. СХЕМА ЭЛЬ-ГАМАЛЯ Пример Шифрование Допустим что
- 15. 2. СХЕМА ЭЛЬ-ГАМАЛЯ Так как в схему
- 16. 2. СХЕМА ЭЛЬ-ГАМАЛЯ Главным преимуществом схемы цифровой
- 17. 2. СХЕМА ЭЛЬ-ГАМАЛЯ Цифровая подпись Эль-Гамаля стала
Слайд 1ЛЕКЦИЯ 8. АСИММЕТРИЧНЫЕ АЛГОРИТМЫ ШИФРОВАНИЯ
КОМПЛЕКСНАЯ БЕЗОПАСНОСТЬ
ИНФОРМАЦИОННЫХ СИСТЕМ
Профессор кафедры
доктор технических наук,
ТУКЕЕВ Дмитрий Леонидович
Слайд 3ЛИТЕРАТУРА
2
1. А.А. ВАРФОЛОМЕЕВ ОСНОВЫ ИНФОРМАЦИОННОЙ БЕЗОПАСНОСТИ
Учебное пособие. Российский университет дружбы
Слайд 43
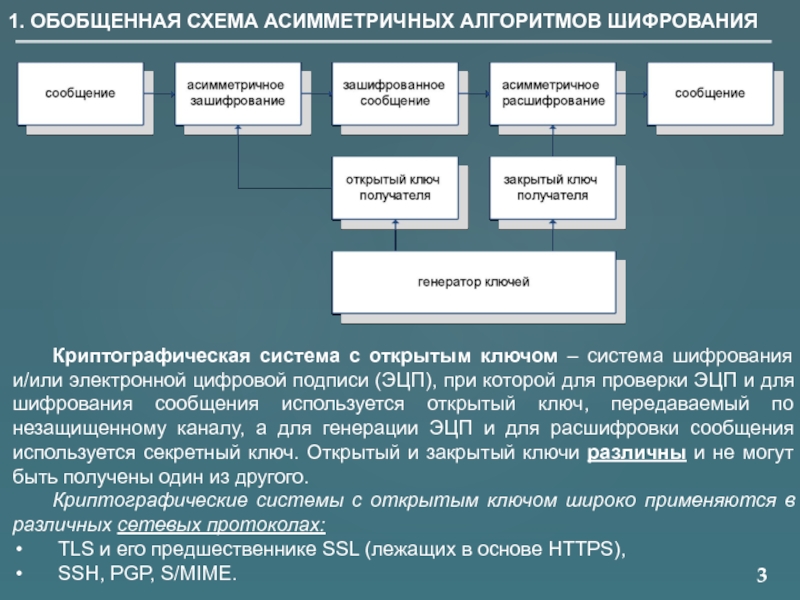
1. ОБОБЩЕННАЯ СХЕМА АСИММЕТРИЧНЫХ АЛГОРИТМОВ ШИФРОВАНИЯ
Криптографическая система с открытым ключом –
Криптографические системы с открытым ключом широко применяются в различных сетевых протоколах:
TLS и его предшественнике SSL (лежащих в основе HTTPS),
SSH, PGP, S/MIME.
Слайд 53
1. ОБОБЩЕННАЯ СХЕМА АСИММЕТРИЧНЫХ АЛГОРИТМОВ ШИФРОВАНИЯ
Односторонние функции
- такие f(x), что по
Криптография с открытым ключом использует односторонние функции с «лазейкой». Лазейка (y) — это некий секрет, который помогает расшифровать. То есть существует такой y, что зная f(x) и y, можно вычислить x.
Пример использования односторонних функций с «лазейкой»
Для шифрования текста можно взять телефонный справочник (по нему очень легко найти номер любого жителя города, но очень сложно по известному номеру найти абонента).
Для каждой буквы из шифруемого сообщения выбирается имя, начинающееся на ту же букву.
Таким образом букве ставится в соответствие номер телефона абонента.
Чтобы расшифровать текст, надо иметь справочник, составленный согласно возрастанию номеров.
Этот справочник является лазейкой (секретом, который помогает получить начальный текст), известной только легальным пользователям.
Слайд 63
1. ОБОБЩЕННАЯ СХЕМА АСИММЕТРИЧНЫХ АЛГОРИТМОВ ШИФРОВАНИЯ
Односторонние функции
Пример односторонней функции – целочисленное
Прямая задача – вычисление произведения двух очень больших чисел P и Q
(N=P*Q) – относительно несложная задача,
Обратная задача – разложение на множители целого числа N является практически неразрешимой при достаточно больших N.
Два типа задач теории чисел, используемых в ассиметр. шифровании:
Факторизация целого числа:
f = x·y, найти x и y, зная f.
На настоящий момент неизвестны алгоритмы факторизации чисел, хотя и не доказано, что таких алгоритмов не существует.
2. Задача дискретного логарифмирования
Для заданных g и a решение x уравнения gx = a называется дискретным логарифмом элемента a по основанию g.
Задача дискретного логарифмирования состоит в нахождении некоторого целого неотрицательного числа x, удовлетворяющего уравнению
gx=a.
Слайд 73
1. ОБОБЩЕННАЯ СХЕМА АСИММЕТРИЧНЫХ АЛГОРИТМОВ ШИФРОВАНИЯ
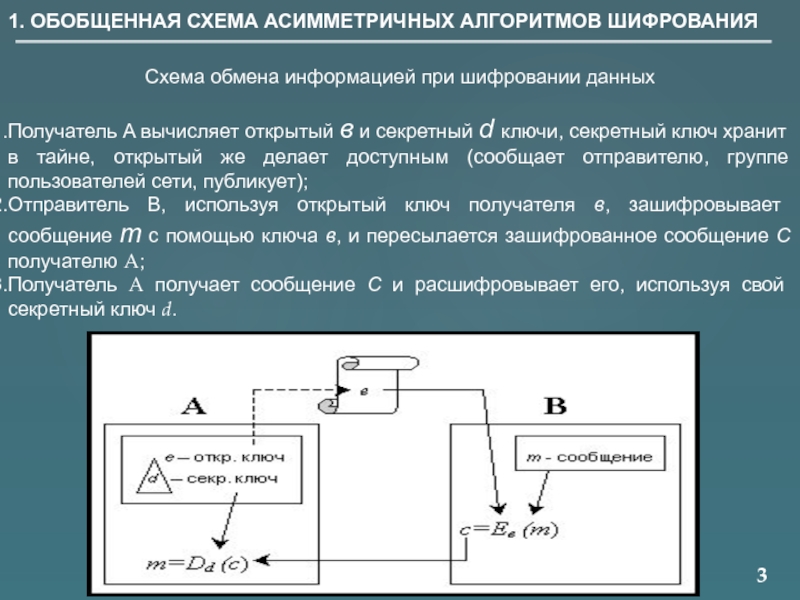
Схема обмена информацией при шифровании данных
Получатель
Отправитель B, используя открытый ключ получателя в, зашифровывает сообщение m c помощью ключа в, и пересылается зашифрованное сообщение С получателю A;
Получатель A получает сообщение С и расшифровывает его, используя свой секретный ключ d.
Слайд 83
1. АЛГОРИТМ ДИФФИ — ХЕЛЛМАНА
ОПИСАНИЕ АЛГОРИТМА
Предположим, существует два абонента: А
A = ga mod p (1)
и пересылает его Б, а Б вычисляет:
B = gb mod p (1)
и передаёт А. Предполагается, что злоумышленник может получить оба этих значения, но не модифицировать их (то есть у него нет возможности вмешаться в процесс передачи).
На втором этапе А на основе имеющегося у нее a и полученного по сети B вычисляет значение:
Ba mod p = gab mod p. (3)
Б на основе имеющегося у него b и полученного по сети A вычисляет значение
Ab mod p = gab mod p. (4)
Его они и могут использовать в качестве секретного ключа, поскольку здесь злоумышленник встретится с практически неразрешимой (за разумное время) проблемой вычисления (3) или (4) по перехваченным ga mod p и gb mod p, если числа p, a, b выбраны достаточно большими.
Слайд 93
1. КРИПТОСИСТЕМА RSA
Криптоалгоритм RSA разработан в 1978 году тремя авторами
В RSA каждый ключ состоит из пары целых чисел.
Каждый участник создает свои открытый и закрытый ключи самостоятельно.
Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их.
Открытый и закрытый ключи каждого участника обмена сообщениями образуют «согласованную пару» в том смысле, что они являются взаимно обратными.
Создание открытого и секретного ключей при использовании алгоритма RSA
1. выбор простых чисел p и q;
2. вычисление n=p·q;
3. вычисление числа m=(p-1)(q-1);
4. выбор открытой экспоненты e , такой, что 1
d·e=1 +к· m;
6. пара чисел P=(e,n) публикуется в качестве открытого ключа;
7. пара S=(d,n) является закрытым (секретным) ключом и держится в секрете.
Слайд 103
1. КРИПТОСИСТЕМА RSA
ПРИМЕР Зашифровать и расшифровать сообщение "САВ" по
РЕШЕНИЕ
Для простоты возьмем небольшие числа - это сократит наши расчеты.
1. Выберем p=3 and q=11.
2. Определим n= 3*11=33.
3. Hайдем (p-1)*(q-1)=20. Следовательно, d будет равно, например, 3: (d=3).
4. Выберем число е по следующей формуле: (e*3) mod 20=1. Значит е будет равно, например, 7: (e=7).
5. Представим шифруемое сообщение как последовательность чисел в диапазоне от 0 до 32 (не забывайте, что кончается на n-1). Буква А =1, В=2, С=3.
Теперь зашифруем сообщение, используя открытый ключ {7,33}
C1 = (3^7) mod 33 = 2187 mod 33 = 9; C2 = (1^7) mod 33 = 1 mod 33 = 1;
C3 = (2^7) mod 33 = 128 mod 33 = 29;
Теперь расшифруем данные, используя закрытый ключ {3,33}.
M1=(9^3) mod 33 =729 mod 33 = 3(С); M2=(1^3) mod 33 =1 mod 33 = 1(А);
M3=(29^3) mod 33 = 24389 mod 33 = 2(В);
Слайд 112. СХЕМА ЭЛЬ-ГАМАЛЯ
Схема Эль-Гамаля (Elgamal) — криптосистема (Elgamal) — криптосистема с открытым ключом, основанная на трудности
Схема была предложена Тахером Эль-ГамалемСхема была предложена Тахером Эль-Гамалем в 1984 году.[1] Эль-Гамаль разработал один из вариантов алгоритма Диффи-Хеллмана. Он усовершенствовал систему Диффи-Хеллмана и получил два алгоритма, которые использовались для шифрования и для обеспечения аутентификации. В отличие от RSA алгоритм Эль-Гамаля не был запатентован и, поэтому, стал более дешевой альтернативой, так как не требовалась оплата взносов за лицензию. Считается, что алгоритм попадает под действие патента Диффи-Хеллмана.
Генерация ключей
Генерируется случайное простое числоГенерируется случайное простое число p длины n битов.
Выбирается случайный примитивный элемент g поля Zp.
Выбирается случайное целое число x такое, что 1
Открытым ключом является тройка (p,g,y), закрытым ключом — число x.
Слайд 122. СХЕМА ЭЛЬ-ГАМАЛЯ
Работа в режиме шифрования
Шифросистема Эль-Гамаля является фактически одним из
Шифрование
Сообщение шифруется следующим образом:
Выбирается сессионный ключ — случайное целое число k такое, что
1
Пара чисел (a,b) является шифротекстом.
Нетрудно видеть, что длина шифротекста в схеме Эль-Гамаля длиннее исходного сообщения вдвое.
Расшифрование
Зная закрытый ключ x, исходное сообщение можно вычислить из шифротекста (a,b) по формуле: M = b(ax)-1 mod p.
При этом нетрудно проверить, что (ax)-1 ≡ g – kx (mod p)
и поэтому b(ax)-1 ≡ (yk M)g – kx ≡ (g kx M) g – kx ≡ M(mod p).
Для практических вычислений больше подходит следующая формула:
M = b(ax)-1 mod p = ba(p-1-x) mod p.
Слайд 142. СХЕМА ЭЛЬ-ГАМАЛЯ
Пример
Шифрование
Допустим что нужно зашифровать сообщение M = 5.
Произведем генерацию ключей:
Выберем x = 8 - случайное целое число x такое, что 1
Итак, открытым является тройка (p,g,y) = (11,2,3), а закрытым ключом является число x = 8.
Выбираем случайное целое число k такое, что 1 < k < (p − 1). Пусть k = 9.
Вычисляем число A = gk mod p = 29 mod 11 = 512 mod 11 = 6.
Вычисляем число B = ykM mod p = 39*5 mod 11 = 19683*5 mod 11 = 9
Полученная пара (a,b) = (6,9) является шифротекстом.
Расшифрование
Необходимо получить сообщение M = 5 по известному шифротексту
(a,b) = (6,9) и закрытому ключу x = 8.
Вычисляем M по формуле
M = b(ax)-1 mod p = 9*(68)-1 mod 11 = 5.
Получили исходное сообщение M = 5.
Слайд 152. СХЕМА ЭЛЬ-ГАМАЛЯ
Так как в схему Эль-Гамаля вводится случайная величина k,то шифр
Для схемы вероятностного шифрования само сообщение M и ключ не определяют шифротекст однозначно. В схеме Эль-Гамаля необходимо использовать различные значения случайной величины k для шифровки различных сообщений M1 и M2.
Если использовать одинаковые k, то для соответствующих шифротекстов (a1,b1) и (a2, b2) выполняется соотношение
b1*(b2)-1 = M1*(M2)-1.
Из этого выражения можно легко вычислить M2, если известно M1.
Слайд 162. СХЕМА ЭЛЬ-ГАМАЛЯ
Главным преимуществом схемы цифровой подписи Эль-Гамаля является возможность вырабатывать
Случайное число k должно сразу после вычисления подписи уничтожаться, так как если злоумышленник знает случайное число k и саму подпись, то он легко может найти секретный ключ по формуле: x = (m-ks)r-1 mod(p-1) и полностью подделать подпись.
Число k должно быть случайным и не должно дублироваться для различных подписей, полученных при одинаковом значении секретного ключа.
Использование свертки m = h(M) объясняется тем, что это защищает подпись от перебора сообщений по известным злоумышленнику значениям подписи.
Пример: если выбрать случайные числа i,j,удовлетворяющие условиям 0
s = r j-1 mod (p-1);
m = r I j-1 mod (p-1),
то легко удостовериться в том, что пара (r,s) является верной цифровой подписью для сообщения x = M.
Слайд 172. СХЕМА ЭЛЬ-ГАМАЛЯ
Цифровая подпись Эль-Гамаля стала примером построения других подписей, схожих
Еще одним из преимуществ является возможность уменьшения длины подписи с помощью замены пары чисел (s,m) на пару чисел (s mod q,m mod q), где q является каким-то простым делителем числа (p-1). При этом сравнение для проверки подписи по модулю p нужно заменить на новое сравнение по модулю q: (yA rB) mod p = gC mod q. Так сделано в американском стандарте DSS (Digital Signature Standard).