- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Графы. Информация и информационные процессы презентация
Содержание
- 1. Графы. Информация и информационные процессы
- 2. Графы «От посёлка Васюки три дороги идут
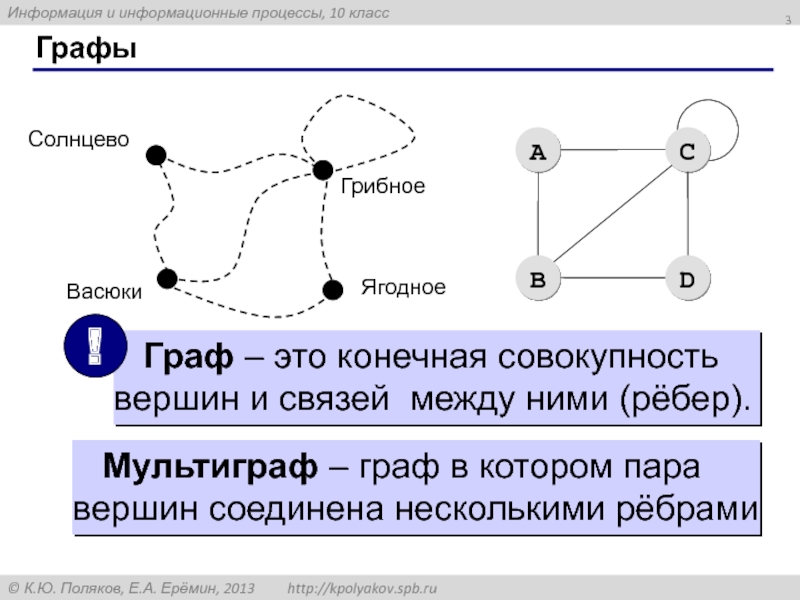
- 3. Графы Мультиграф – граф в котором пара вершин соединена несколькими рёбрами
- 4. Граф (англ. graph) — совокупность непустого множества вершин и наборов пар
- 5. Граф, или неориентированный граф G— это
- 6. Вершины и рёбра графа называются также
- 7. Два ребра называются кратными, если множества
- 8. А B D C E 3
- 9. Теорема о сумме степеней вершин графа Сумма
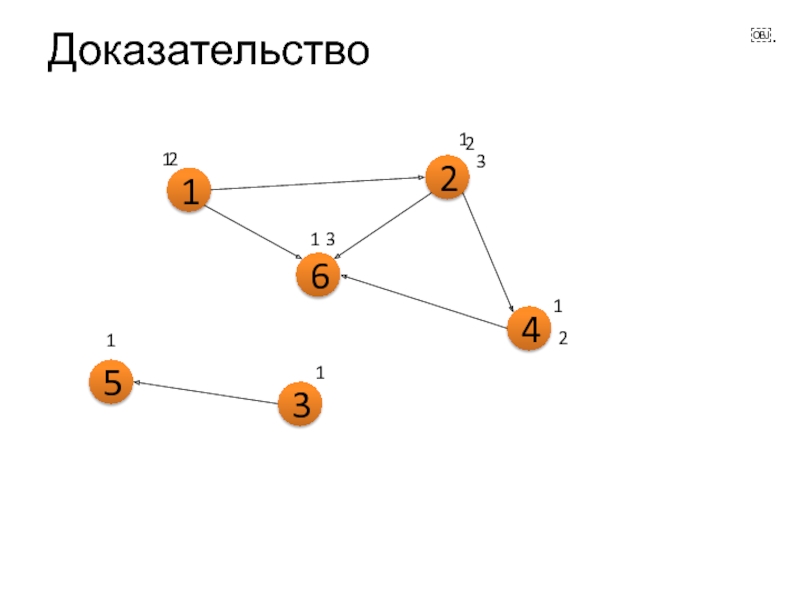
- 10. Доказательство 1 2 4 6 1 1 2 1 1 2 3 2 3
- 11. Доказательство 1 2 4 6 1 1
- 12. для ориентированного графа:
- 13. Доказательство 1 2 4 6 1 1
- 14. Лемма о рукопожатиях В любом графе число
- 15. Теорема о существовании вершин одинаковой степени В
- 16. Теорема о существовании вершин одинаковой степени
- 17. Матрица и список смежности петля Матрица
- 18. Способы представления графа в информатике Матрица смежности
- 19. Способы представления графа в информатике Список смежности —каждой
- 20. Маршрутом в графе называют конечную последовательность вершин, в
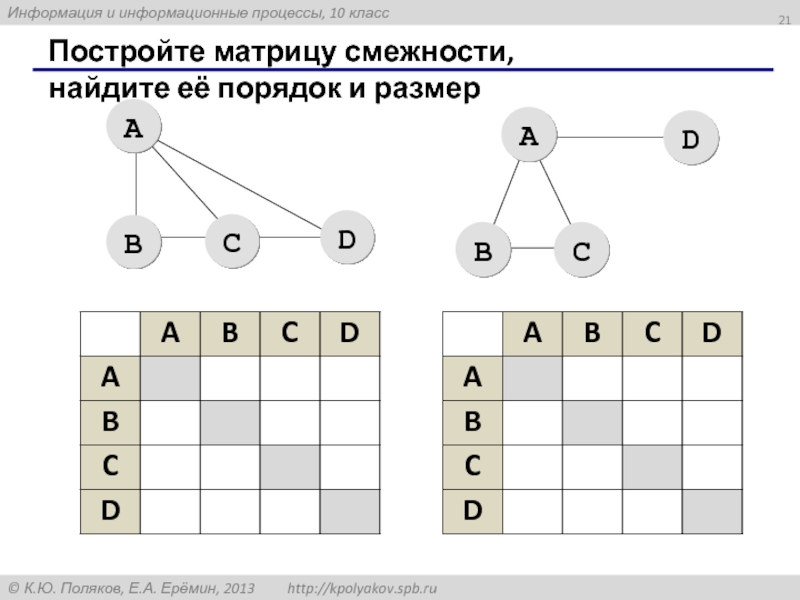
- 21. Постройте матрицу смежности, найдите её порядок и размер
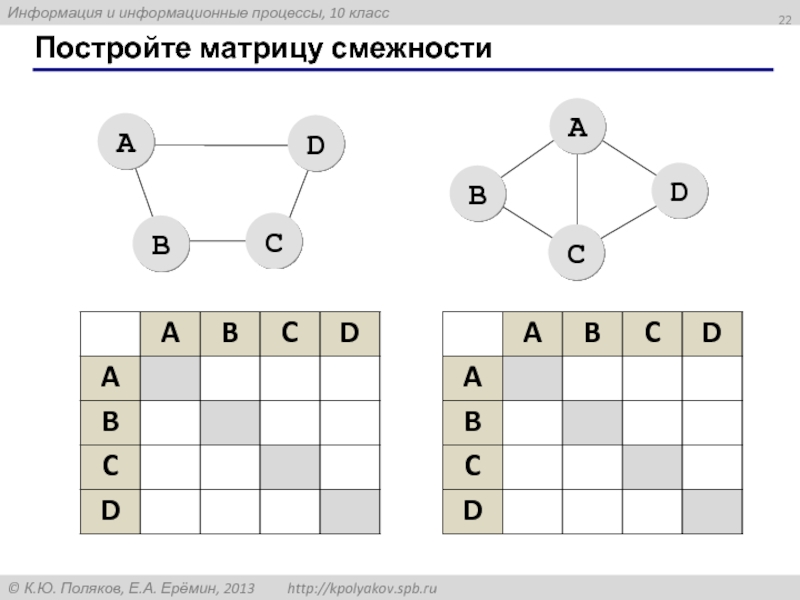
- 22. Постройте матрицу смежности
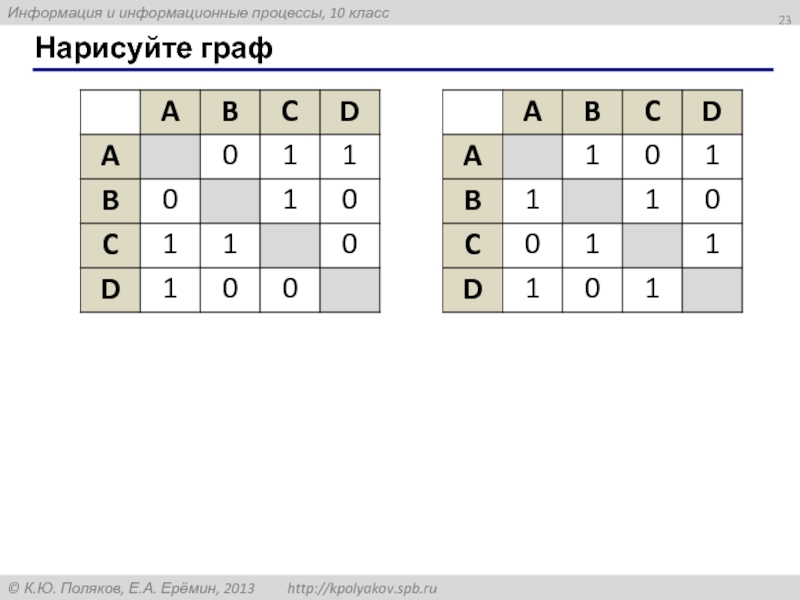
- 23. Нарисуйте граф
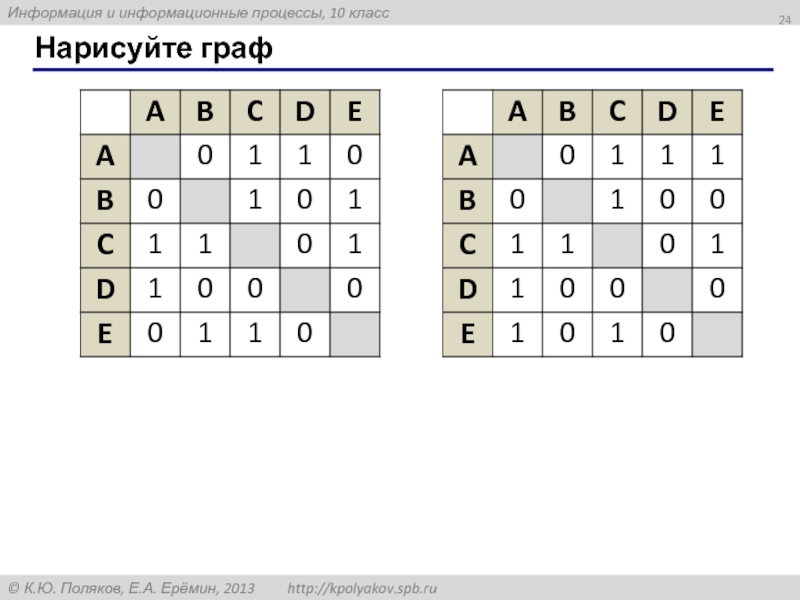
- 24. Нарисуйте граф
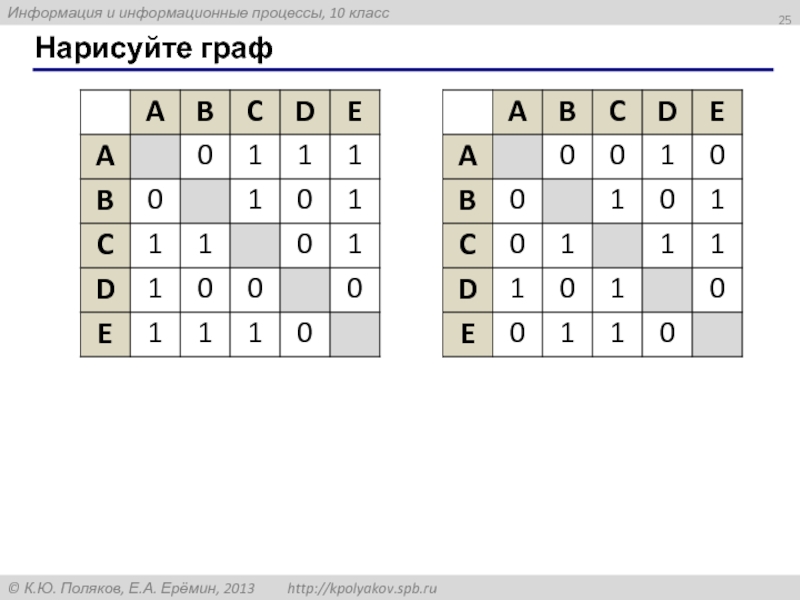
- 25. Нарисуйте граф
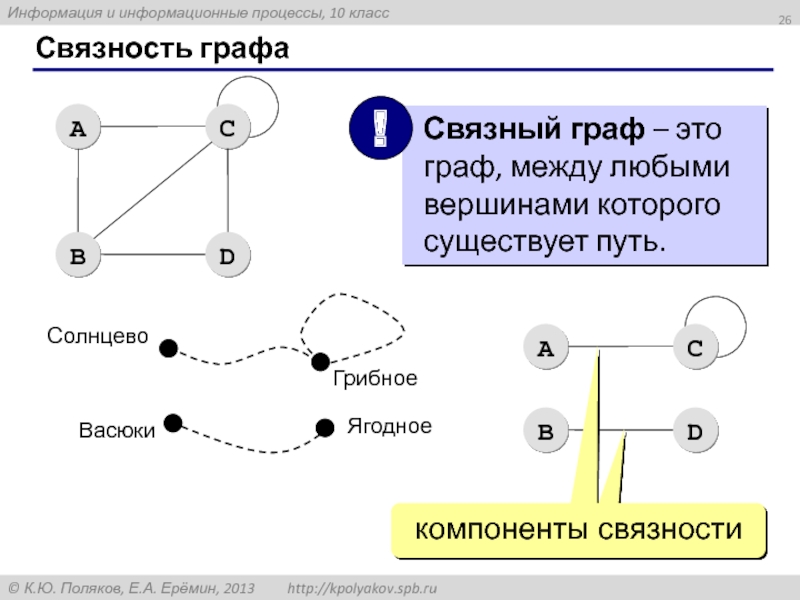
- 26. Связность графа
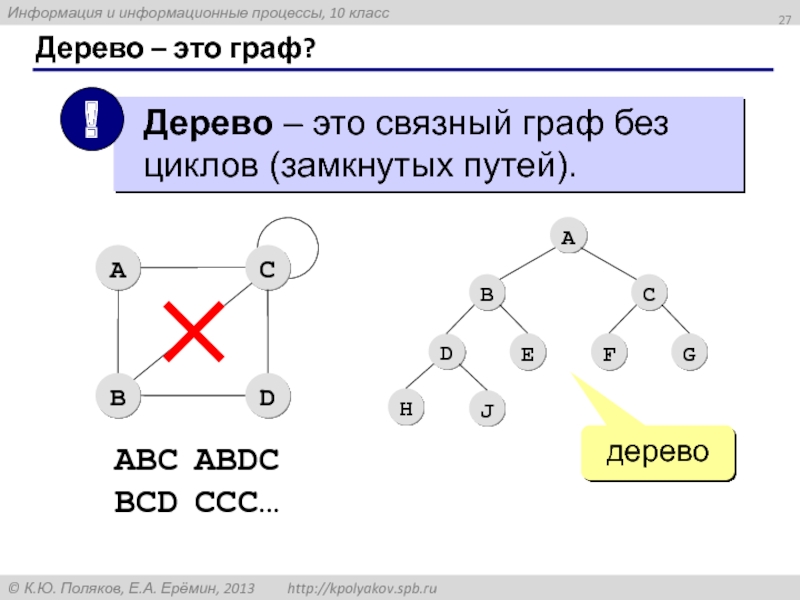
- 27. Дерево – это граф? дерево ABC ABDC BCD CCC…
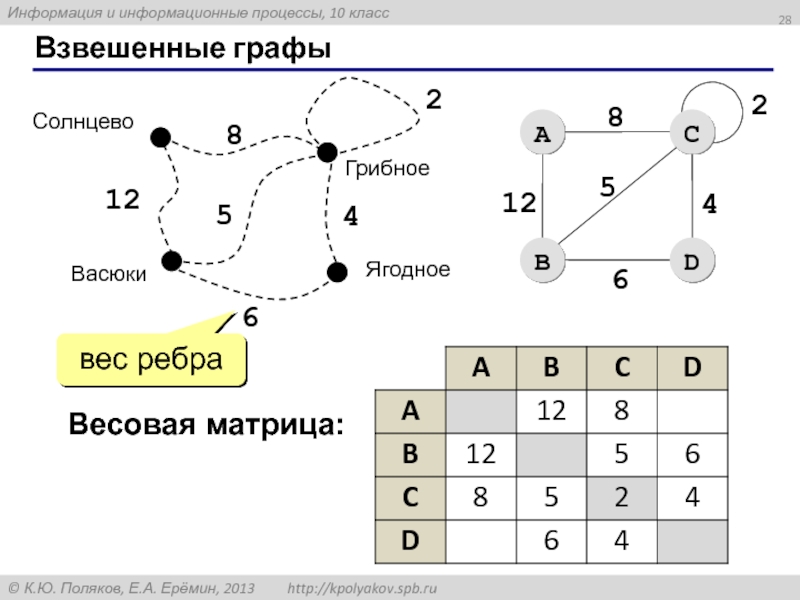
- 28. Взвешенные графы 12 8 2 5 4 6 Весовая матрица: вес ребра
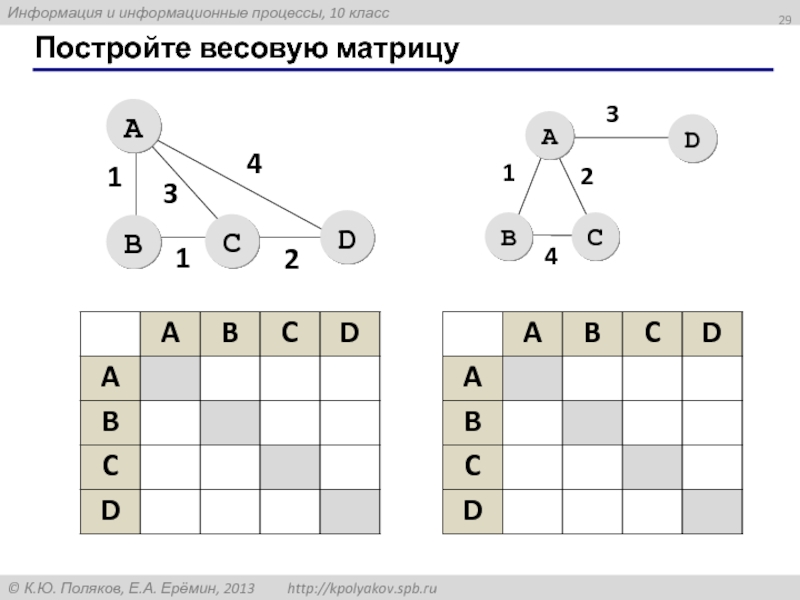
- 29. Постройте весовую матрицу
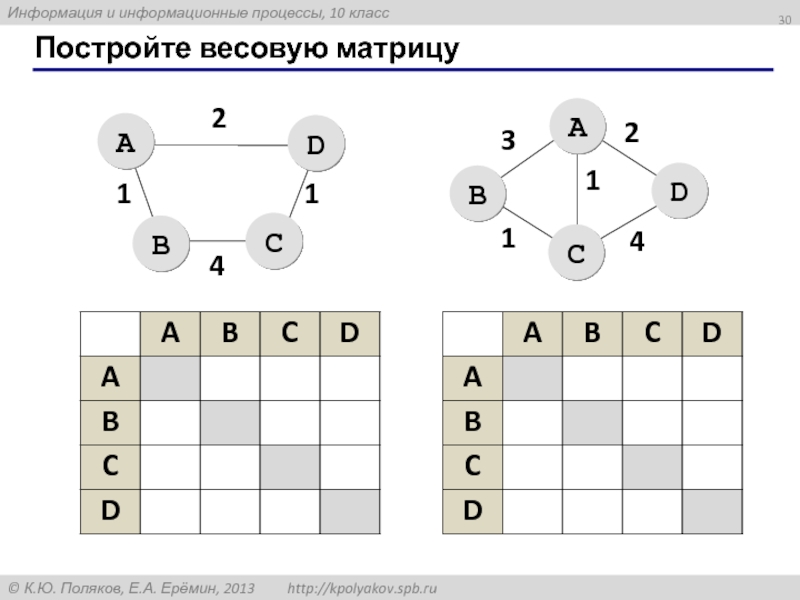
- 30. Постройте весовую матрицу
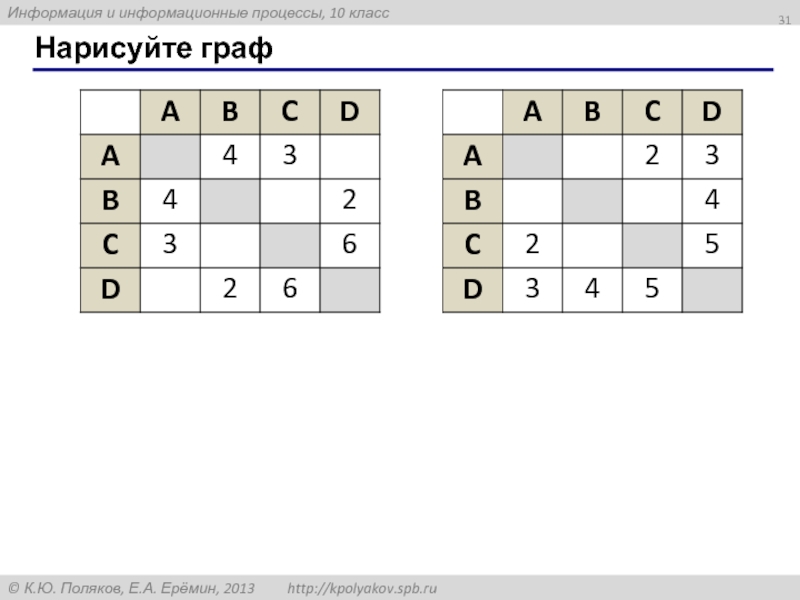
- 31. Нарисуйте граф
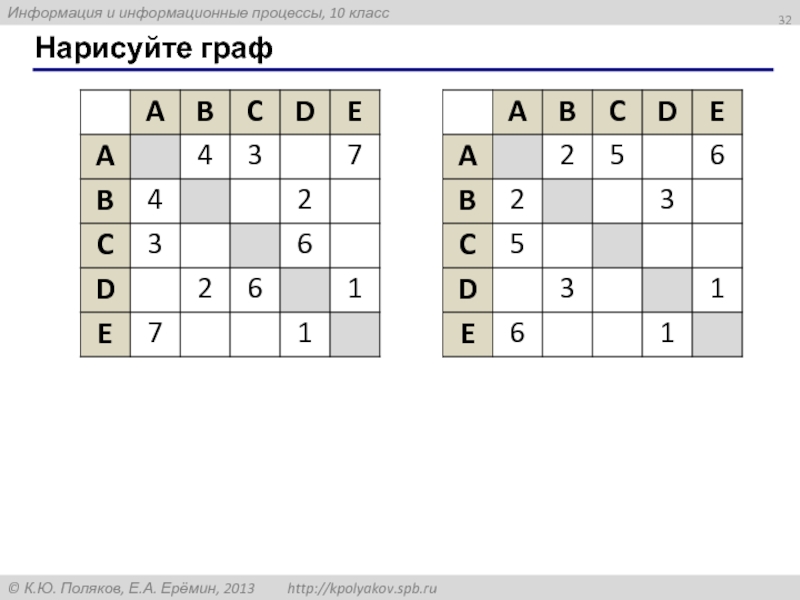
- 32. Нарисуйте граф
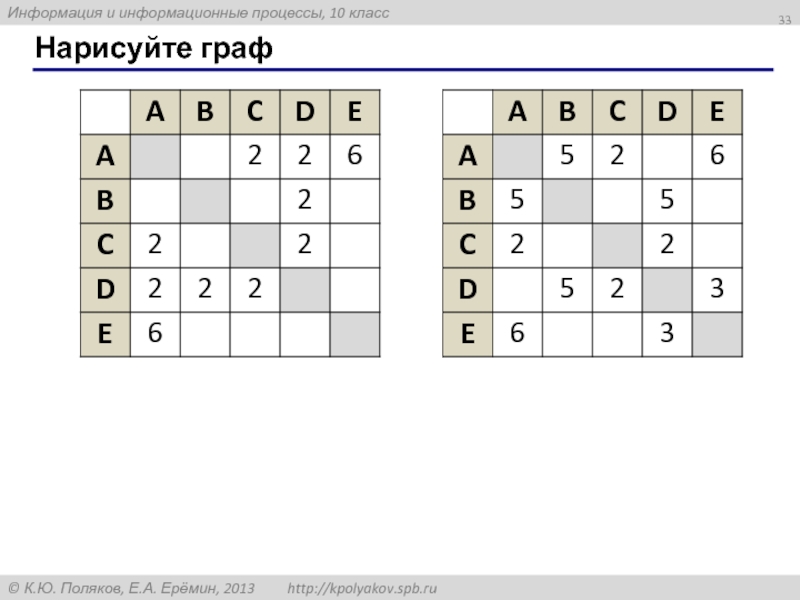
- 33. Нарисуйте граф
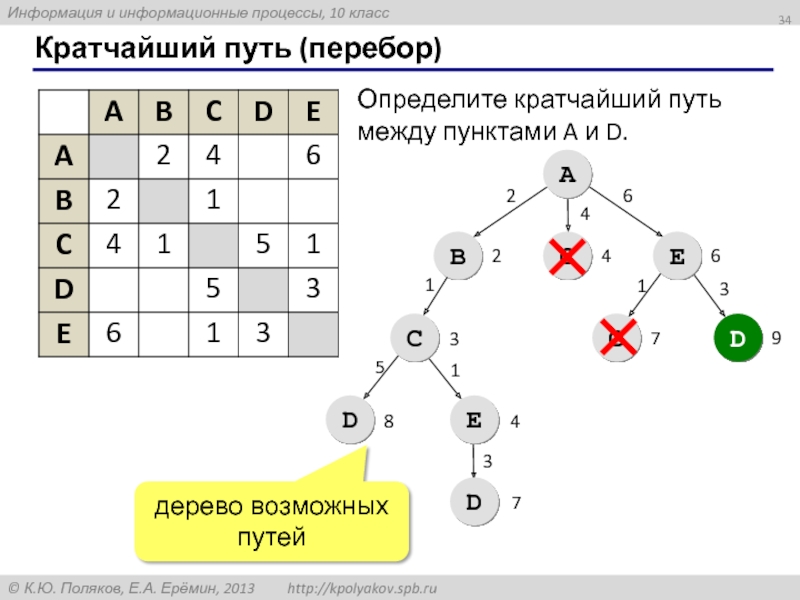
- 34. Кратчайший путь (перебор)
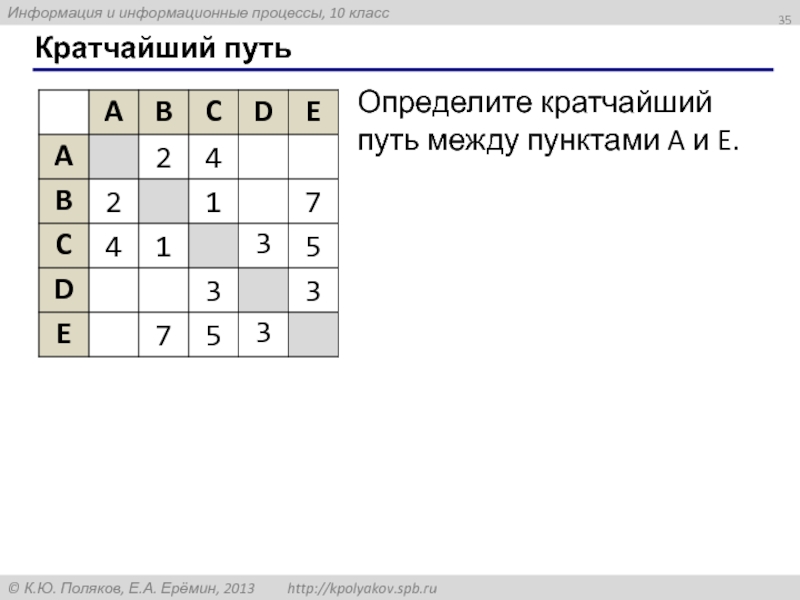
- 35. Кратчайший путь Определите кратчайший путь между пунктами A и E.
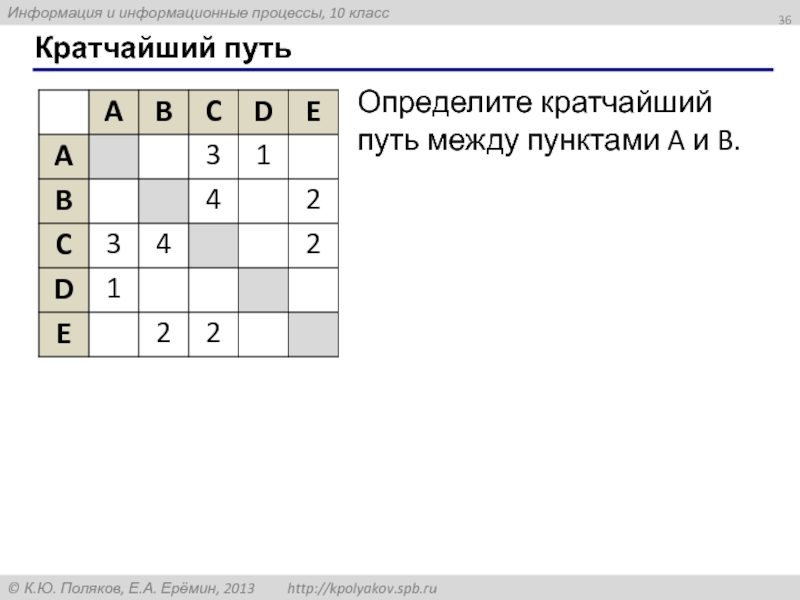
- 36. Кратчайший путь Определите кратчайший путь между пунктами A и B.
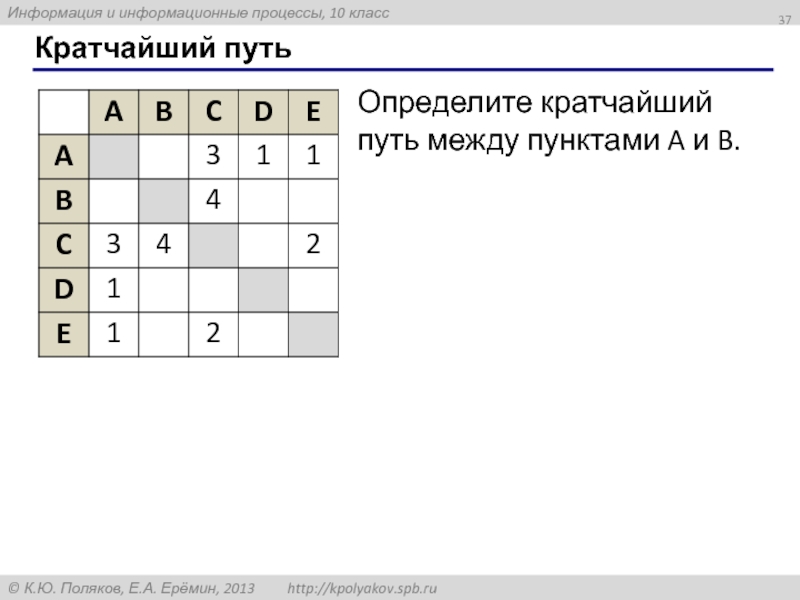
- 37. Кратчайший путь Определите кратчайший путь между пунктами A и B.
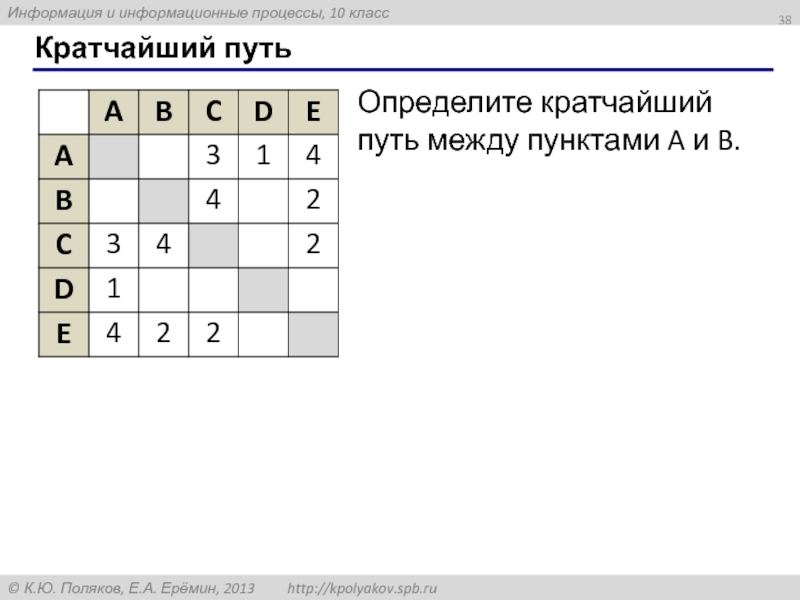
- 38. Кратчайший путь Определите кратчайший путь между пунктами A и B.
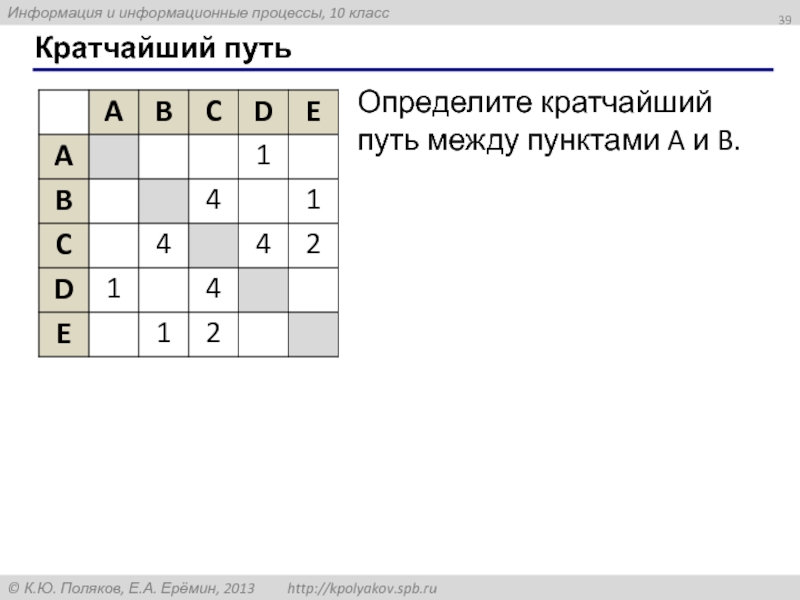
- 39. Кратчайший путь Определите кратчайший путь между пунктами A и B.
- 40. Ориентированные графы (орграфы) Рёбра имеют направление (начало и конец), рёбра называю дугами.
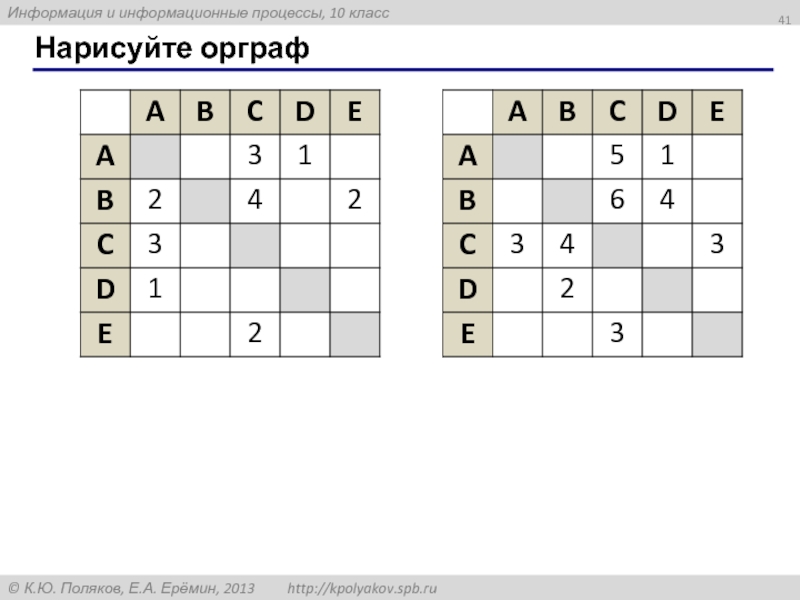
- 41. Нарисуйте орграф
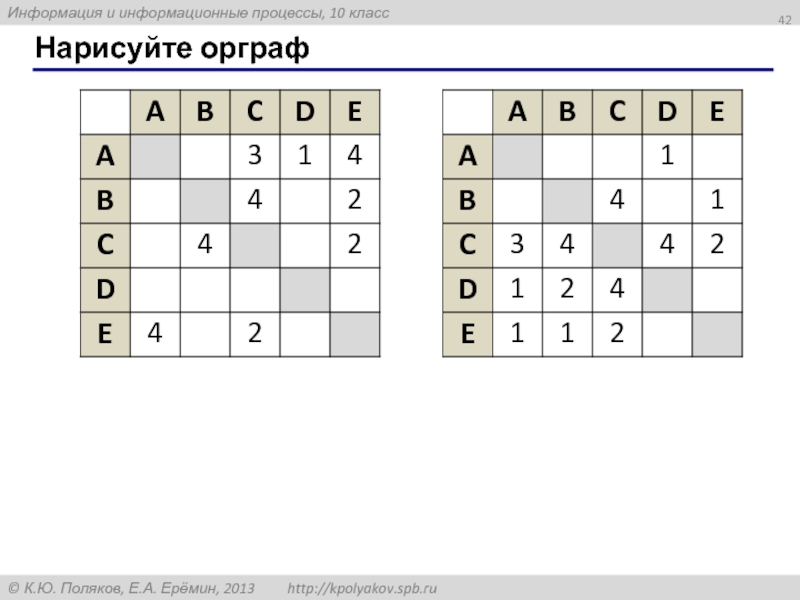
- 42. Нарисуйте орграф
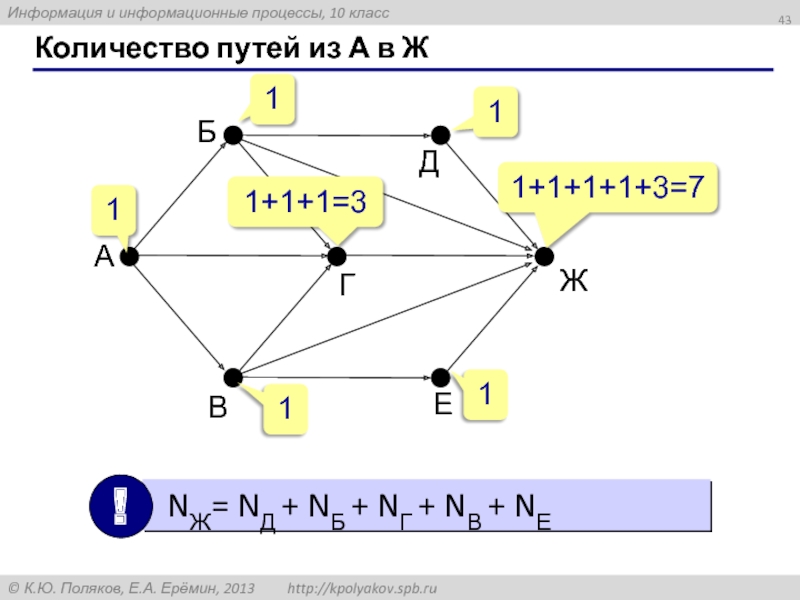
- 43. Количество путей из А в Ж 1 1 1 1+1+1=3 1 1+1+1+1+3=7 1
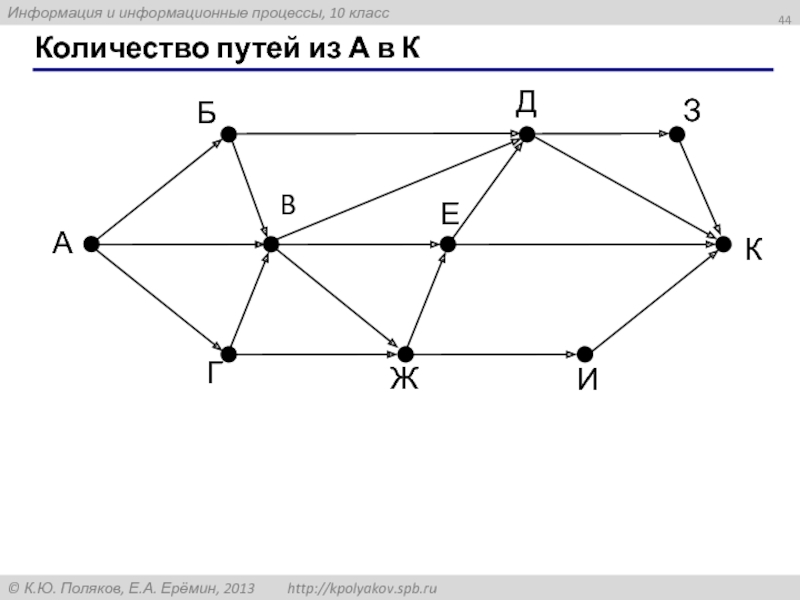
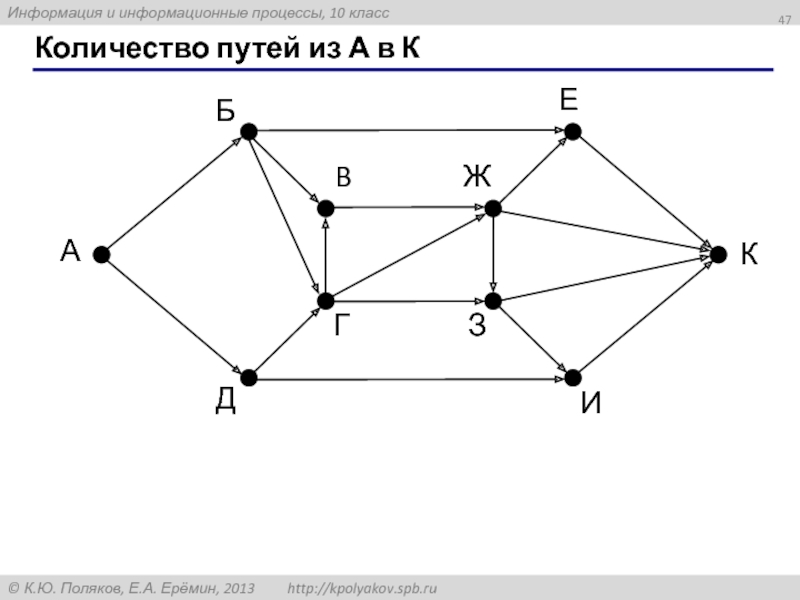
- 44. Количество путей из А в К
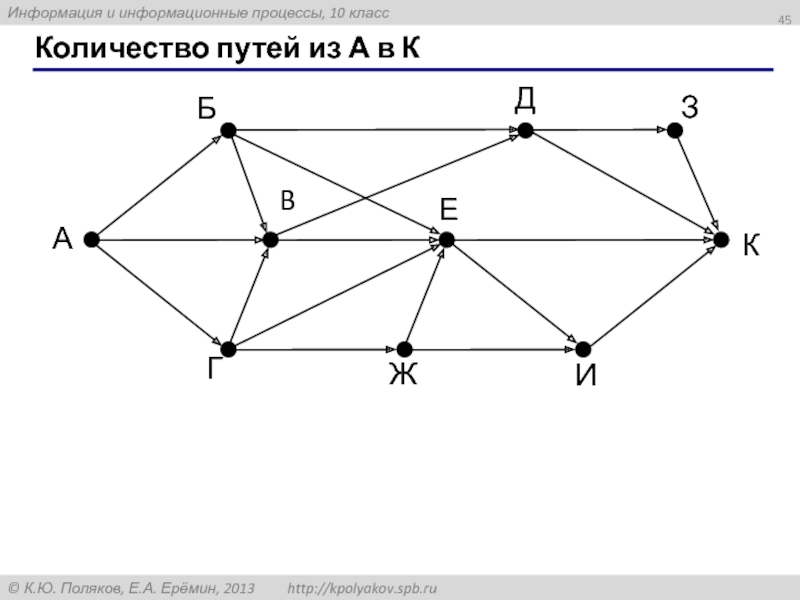
- 45. Количество путей из А в К
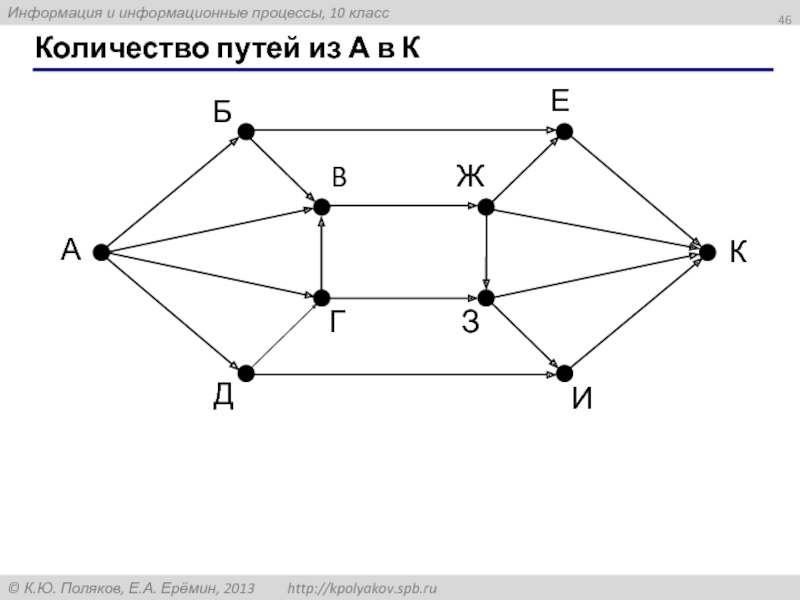
- 46. Количество путей из А в К
- 47. Количество путей из А в К
- 48. Количество путей из А в Л не
- 49. Количество путей из А в Л через
- 50. Количество путей из А в Л через
- 51. Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель
- 52. Источники иллюстраций http://overhealth.ru https://ufhealth.org http://wmposters.com
Слайд 2Графы
«От посёлка Васюки три дороги идут в посёлки Солнцево, Грибное и
Ягодное. Между Солнцевым и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное».
Слайд 4
Граф (англ. graph) — совокупность непустого множества вершин и наборов пар вершин (связей между вершинами); основной
объект изучения математической теории графов.
От греч. γράφω «царапаю, черчу, пишу»:
Граф (математика) — объект, состоящий из вершин и соединяющих их рёбер.
От греч. γράφω «царапаю, черчу, пишу»:
Граф (математика) — объект, состоящий из вершин и соединяющих их рёбер.
Слайд 5
Граф, или неориентированный граф G— это упорядоченная пара G:=(V,E), где V
— это непустое множество вершин или узлов, а E — множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.
V (а значит и E), обычно считаются конечными множествами. Многие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов, поскольку не все утверждения, имеющие место для конечных совокупностей, выполняются в случае бесконечных множеств.
V (а значит и E), обычно считаются конечными множествами. Многие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов, поскольку не все утверждения, имеющие место для конечных совокупностей, выполняются в случае бесконечных множеств.
Слайд 6
Вершины и рёбра графа называются также элементами графа,
число вершин в
графе |V| — порядком,
число рёбер |E| — размером графа.
Вершины u и v называются концевыми вершинами (или просто концами) ребра e={u,v}. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.
Два ребра называются смежными, если они имеют общую концевую вершину.
число рёбер |E| — размером графа.
Вершины u и v называются концевыми вершинами (или просто концами) ребра e={u,v}. Ребро, в свою очередь, соединяет эти вершины. Две концевые вершины одного и того же ребра называются соседними.
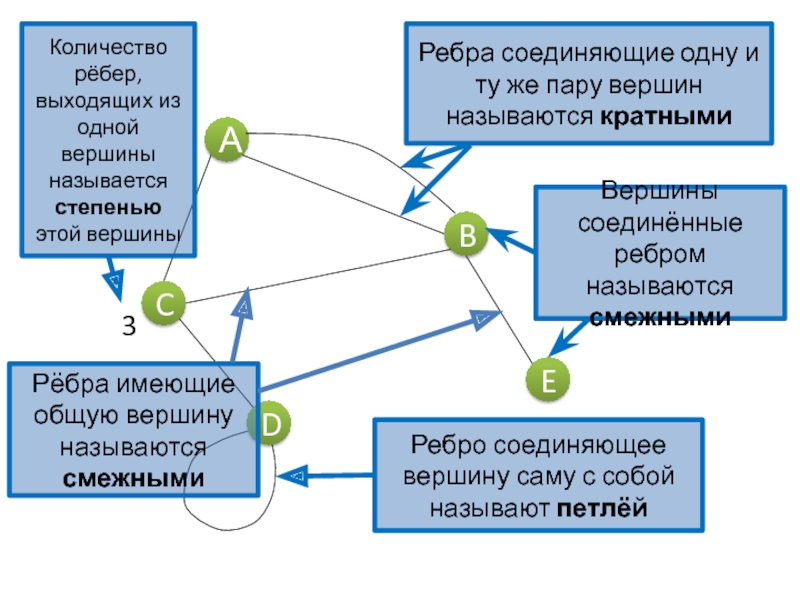
Два ребра называются смежными, если они имеют общую концевую вершину.
Слайд 7
Два ребра называются кратными, если множества их концевых вершин совпадают.
Ребро называется
петлёй, если его концы совпадают, то есть e={v,v}.
Степенью deg V вершины V называют количество инцидентных ей рёбер (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра;
Вершина называется висячей (или листом), если она является концом ровно одного ребра.
Степенью deg V вершины V называют количество инцидентных ей рёбер (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра;
Вершина называется висячей (или листом), если она является концом ровно одного ребра.
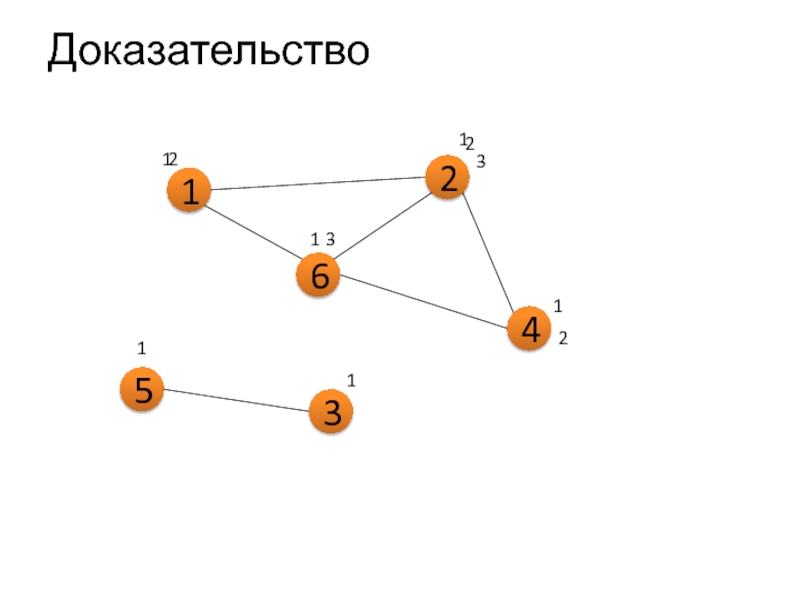
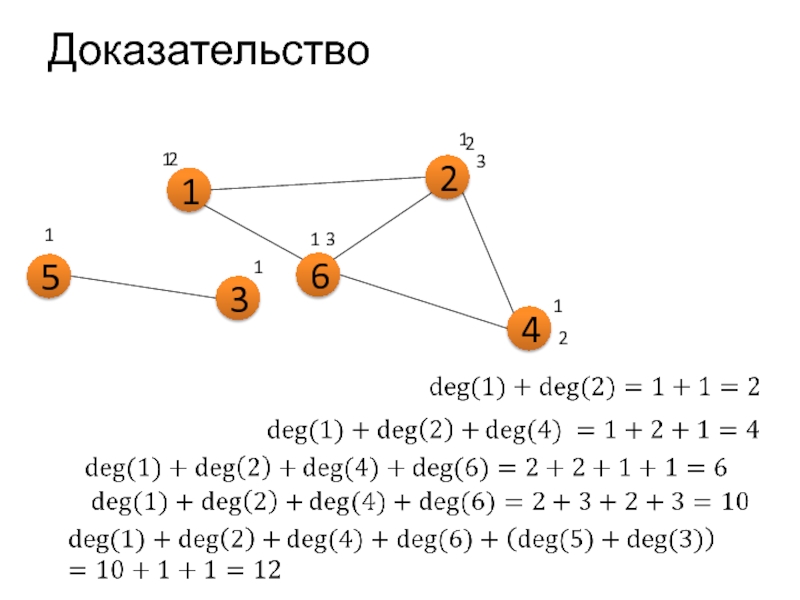
Слайд 9Теорема о сумме степеней вершин графа
Сумма степеней всех вершин графа (или
мультиграфа без петель) — равна удвоенному числу рёбер
для неориентированного графа
Если взять вершины, вообще не связанные друг с другом, то сумма степеней этих вершин равна нулю.
Прибавляя любое ребро, которое связывает две вершины, увеличиваем сумму всех степеней на 2 единицы.
Таким образом, сумма всех степеней вершин четна и равна удвоенному количеству рёбер.
Слайд 14Лемма о рукопожатиях
В любом графе число вершин нечётной степени чётно.
В любой
момент времени количество людей, сделавших нечетное число рукопожатий, чётно
Сумма степеней всех вершин в графе (или мультиграфе без петель) должна быть четной.
Удаляя из этой суммы степени четных вершин, получим, что сумма степеней нечетных вершин, должна быть четной.
Значит, само число таких вершин должно быть четным.
Лемма доказана.
Слайд 15Теорема о существовании вершин одинаковой степени
В любом графе есть по крайней
мере две вершины, имеющие одинаковую степень.
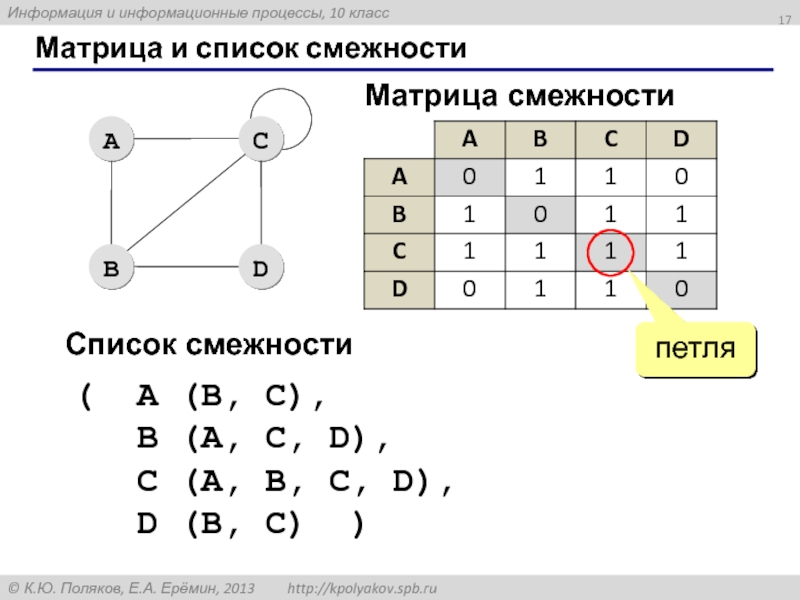
Слайд 17Матрица и список смежности
петля
Матрица смежности
Список смежности
( A (B, C),
B (A, C, D),
C (A, B, С, D),
D (B, C) )
Слайд 18Способы представления графа в информатике
Матрица смежности - бинарная матрица каждой ячейке
которой записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).
Это наиболее удобный способ представления плотных графов.
Недостатком являются требования к памяти, прямо пропорциональные квадрату количества вершин.
Это наиболее удобный способ представления плотных графов.
Недостатком являются требования к памяти, прямо пропорциональные квадрату количества вершин.
Слайд 19Способы представления графа в информатике
Список смежности —каждой вершине графа соответствует список, состоящий
из "соседей" этой вершины.
Реализация предложенная Гвидо ван Россумом использует хэш-таблицу для ассоциации каждой вершины со списком смежных вершин. Нет явного представления рёбер в этой структуре
Кормен и другие предложили реализацию в которой вершины представлены числовым индексом в массиве, в котором каждая ячейка массива ссылается на однонаправленный связанный список соседних вершин.
Объектно ориентированный список смежности, предложенный Гудричем и Таммасией, содержит специальные классы вершин и рёбер. Каждый объект вершины содержит ссылку на коллекцию рёбер. Каждый объект ребра содержит ссылки на исходящую и входящую вершины.
Слайд 20Маршрутом в графе называют конечную последовательность вершин, в которой каждая вершина (кроме
последней) соединена со следующей в последовательности вершиной ребром.
Цепью называется маршрут без повторяющихся рёбер.
Ориентированным маршрутом (или путём) в орграфе называют конечную последовательность вершин и дуг, в которой каждый элемент инцидентен предыдущему и последующему.
Циклом называют цепь, в которой первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер.
Путь (или цикл) называют простым, если рёбра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются.
Цепью называется маршрут без повторяющихся рёбер.
Ориентированным маршрутом (или путём) в орграфе называют конечную последовательность вершин и дуг, в которой каждый элемент инцидентен предыдущему и последующему.
Циклом называют цепь, в которой первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер.
Путь (или цикл) называют простым, если рёбра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются.
Слайд 34Кратчайший путь (перебор)
A
B
С
E
С
D
С
D
E
D
2
4
6
2
4
6
1
3
1
3
9
7
5
8
4
1
3
7
дерево возможных путей
Определите кратчайший путь между пунктами A и
D.
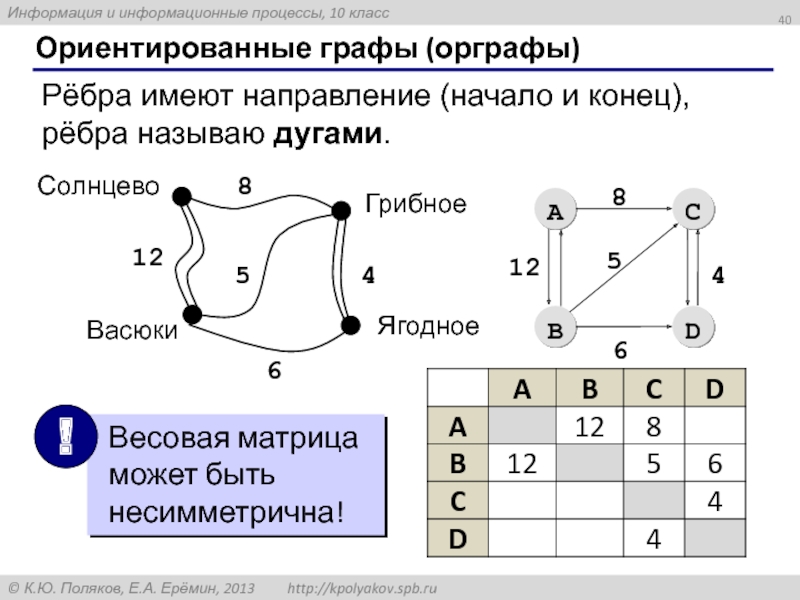
Слайд 40Ориентированные графы (орграфы)
Рёбра имеют направление (начало и конец), рёбра называю дугами.
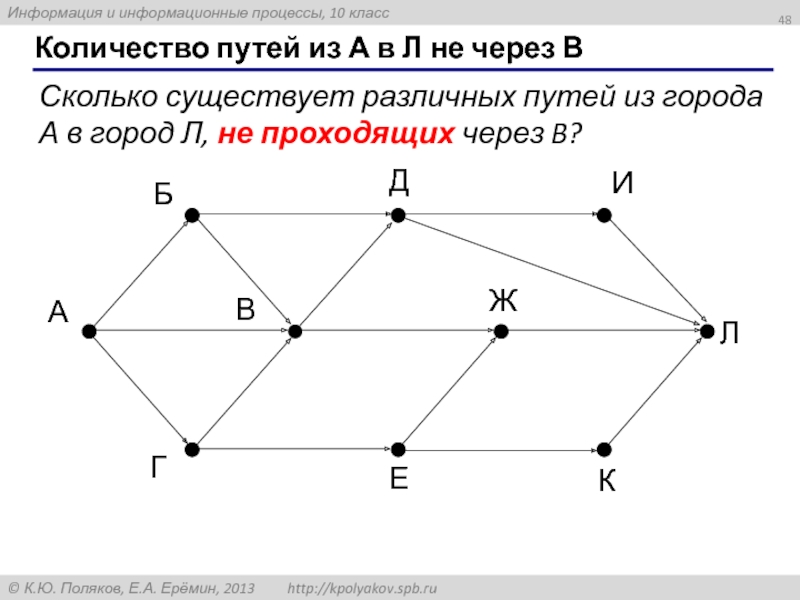
Слайд 48Количество путей из А в Л не через В
А
Б
В
Г
Д
Е
Ж
И
К
Л
Сколько существует различных
путей из города А в город Л, не проходящих через B?
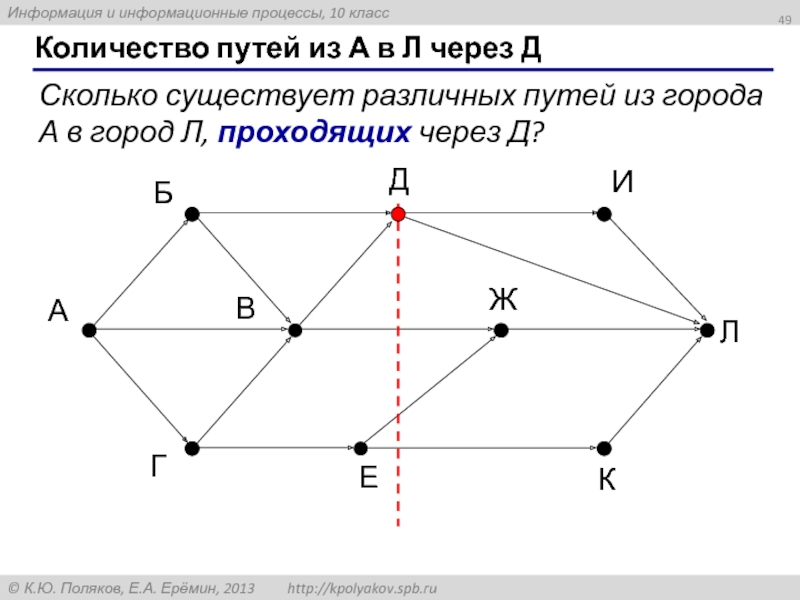
Слайд 49Количество путей из А в Л через Д
А
Б
В
Г
Д
Е
Ж
И
К
Л
Сколько существует различных путей
из города А в город Л, проходящих через Д?
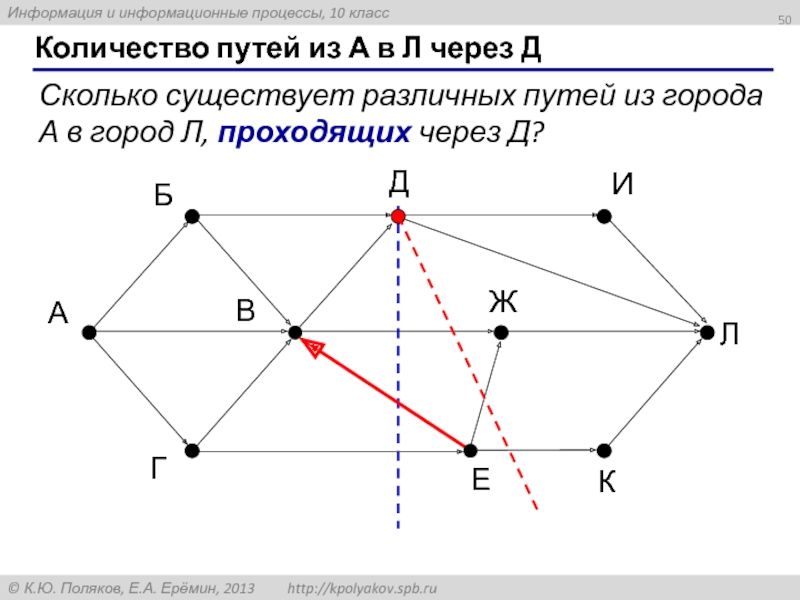
Слайд 50Количество путей из А в Л через Д
Сколько существует различных путей
из города А в город Л, проходящих через Д?
А
Б
В
Г
Д
Е
Ж
И
К
Л
Слайд 51Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г. Санкт-Петербург
kpolyakov@mail.ru
ЕРЕМИН Евгений Александрович
к.ф.-м.н., доцент кафедры мультимедийной дидактики и ИТО ПГГПУ, г. Пермь
eremin@pspu.ac.ru
к.ф.-м.н., доцент кафедры мультимедийной дидактики и ИТО ПГГПУ, г. Пермь
eremin@pspu.ac.ru
Слайд 52Источники иллюстраций
http://overhealth.ru
https://ufhealth.org
http://wmposters.com
http://ozon.ru
http://www.bikeshot.ru
http://ru.wikipedia.org
http://salestores.com
http://gimp-werkstatt.de
http://frontal-cortex.tumblr.com
http://www.intermedia.kg
http://pc-azbuka.ru
авторские материалы
