- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрическая интерпретация ЗЛП. (Тема 4) презентация
Содержание
- 1. Геометрическая интерпретация ЗЛП. (Тема 4)
- 2. Основные определения Точка А называется линейной
- 3. Множество называется замкнутым, если оно содержит
- 4. Геометрическая интерпретация задач линейного программирования
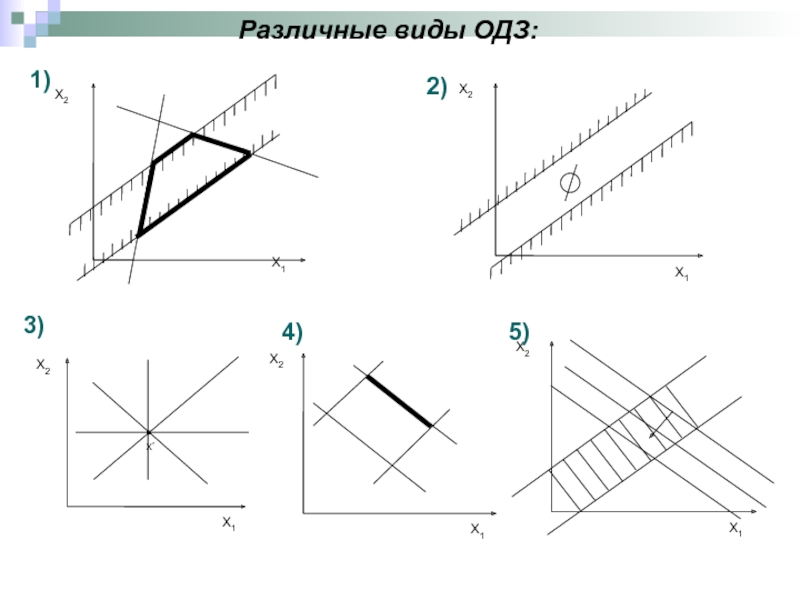
- 5. Различные виды ОДЗ: 1) 3) 2) 4) 5)
- 7. Геометрический способ решения ЗЛП 2 случая:
- 8. 2)n - m=2 В системе ограничений надо выделить исходный базис.
Слайд 2Основные определения
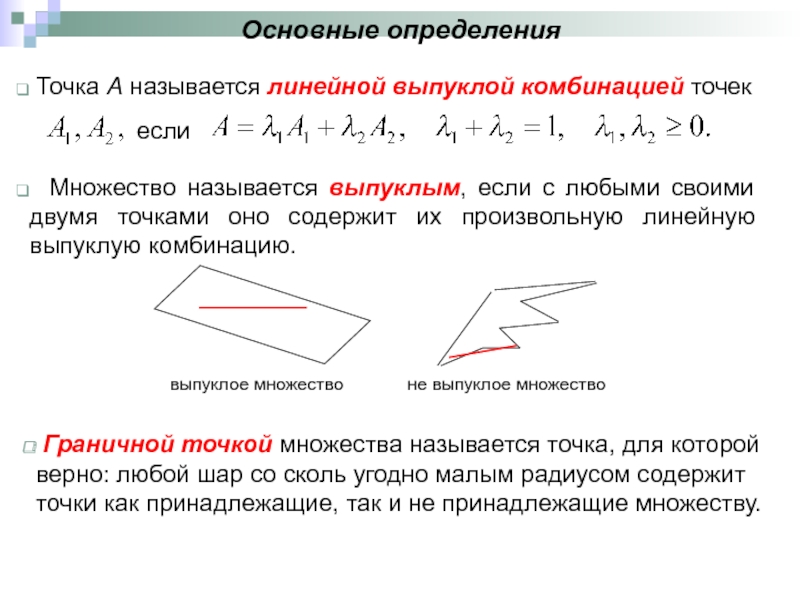
Точка А называется линейной выпуклой комбинацией точек
если
Множество называется
выпуклое множество не выпуклое множество
Граничной точкой множества называется точка, для которой верно: любой шар со сколь угодно малым радиусом содержит точки как принадлежащие, так и не принадлежащие множеству.
Слайд 3 Множество называется замкнутым, если оно содержит все свои граничные точки.
Точка называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации двух различных точек этого множества.
Ограниченное выпуклое замкнутое множество на плоскости с конечным числом вершин называется выпуклым многоугольником.
Теорема Выпуклый замкнутый ограниченный многогранник является выпуклой линейной комбинацией своих угловых точек.
Лемма Пересечение любого количества выпуклых множеств является выпуклым множеством.
Слайд 6
(градиент) f = grad(f) – вектор из частных производных =
Градиент всегда показывает направление возрастания функции. Вектор градиент функции в точке всегда перпендикулярен касательной.
Слайд 9
Свойства решений ЗЛП
Теорема 1 ОДЗ
Теорема 2 Целевая функция ЗЛП достигает своего минимального (максимального) значения в угловой точке многогранника решений. Если целевая функция достигает своего экстремального значения более чем в одной угловой точке многогранника решений, то она достигает того же значения в любой линейной выпуклой комбинации этих угловых точек.