- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы теории полезности презентация
Содержание
- 1. Элементы теории полезности
- 2. СОДЕРЖАНИЕ Текущий контроль Функции полезности Аксиомы линейной полезности Многофакторная полезность
- 3. Определить лузера – претендента, который не может победить Здесь i– порядковый номер студента.
- 4. Цели и средства Цель: дать количественную
- 5. Функции и аксиомы полезности Функция
- 6. Альтернативы риска Совершенная функция полезности – это
- 7. Линейная комбинация альтернатив Линейной комбинацией альтернатив P
- 8. Пример. Заданы распределения P и Q: Исходные распределения: Линейная комбинация:
- 9. Аксиомы функции полезности Ниже полагаем:
- 10. САМОСТОЯТЕЛЬНО Построить график вспомогательной функции V применительно
- 11. Принятие наиболее полезных решений Содержательная постановка задачи:
- 12. Обозначения R – величина ресурса;
- 13. Формальная постановка задачи
- 14. Преобразование системы (1) Пусть
- 15. ПРИМЕР 1 Уложить в рюкзак наиболее
- 16. Формальная постановка задачи
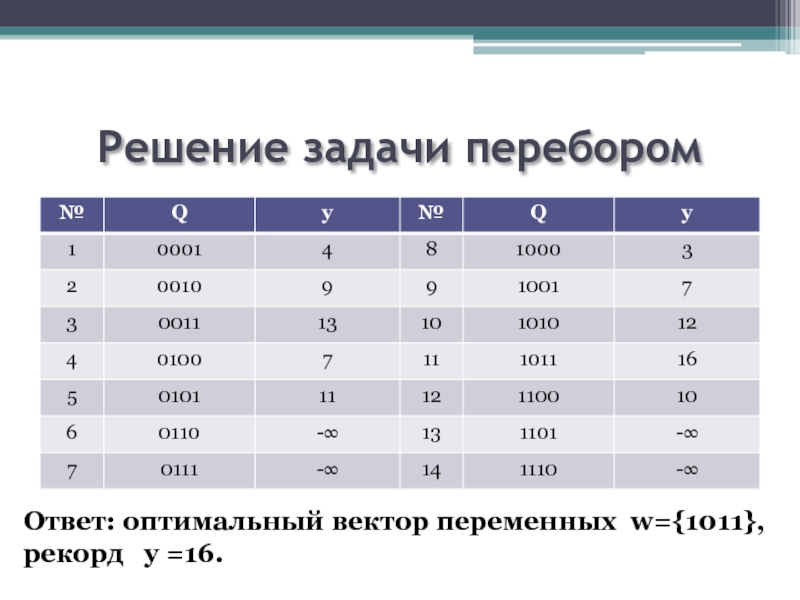
- 17. Решение задачи перебором Ответ: оптимальный вектор переменных w={1011}, рекорд y =16.
- 18. Решить самостоятельно Выбрать наиболее полезные направления развития
- 19. Многофакторная полезность Часто полезность является функцией не
- 20. Аддитивная многофакторная функция полезности Функция
- 21. Эквивалентные векторы Векторы (x1, x2, ..., xm)
- 22. Многофакторная полезность Дать формальное описание задачи и
- 23. Максимальная полезность i-го объекта Формальная постановка задачи:
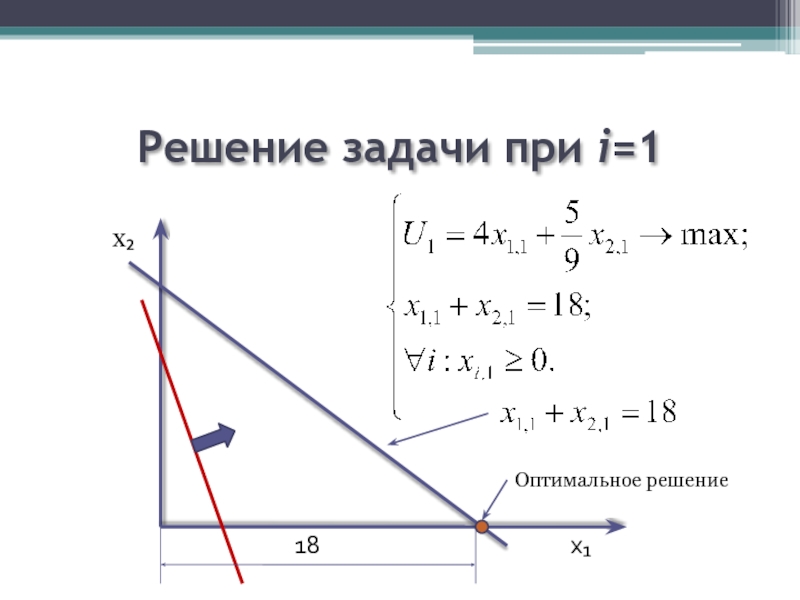
- 24. Решение задачи при i=1
- 25. Решить самостоятельно На множестве из трех направлений
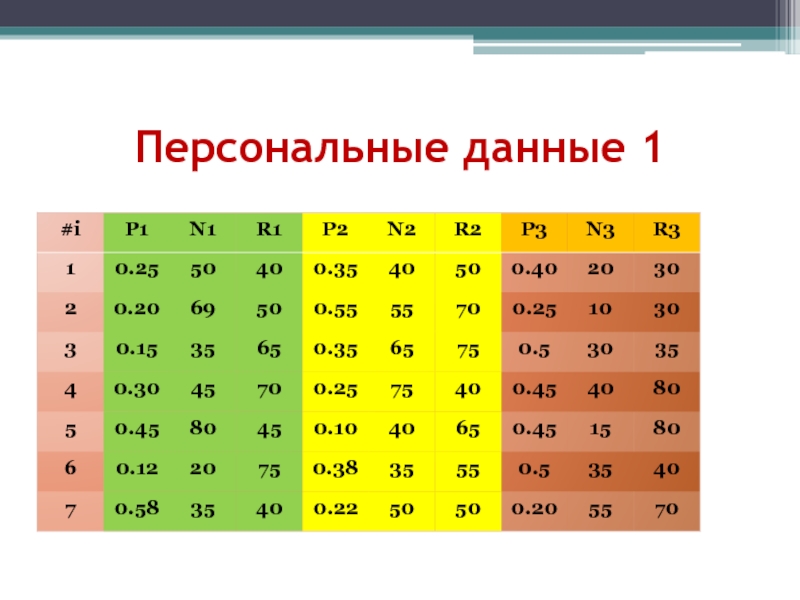
- 26. Персональные данные 1
- 27. Персональные данные 2
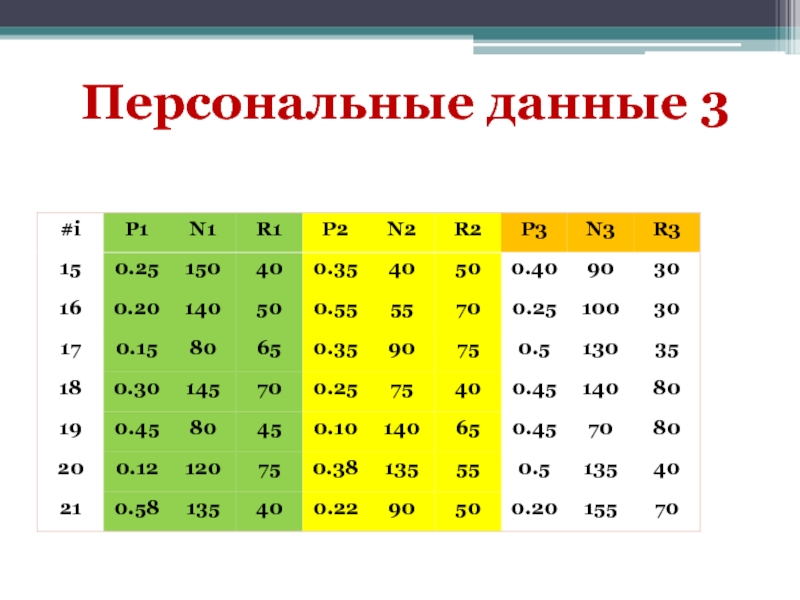
- 28. Персональные данные 3
Слайд 2СОДЕРЖАНИЕ
Текущий контроль
Функции полезности
Аксиомы линейной полезности
Многофакторная полезность
Слайд 3Определить лузера – претендента, который не может победить
Здесь i– порядковый номер
Слайд 4Цели и средства
Цель: дать количественную оценку отношению предпочтения и определить
Инструмент: распределение имеющихся ресурсов.
Результат: наибольшая полезность выигрыша.
Слайд 5Функции и аксиомы полезности
Функция
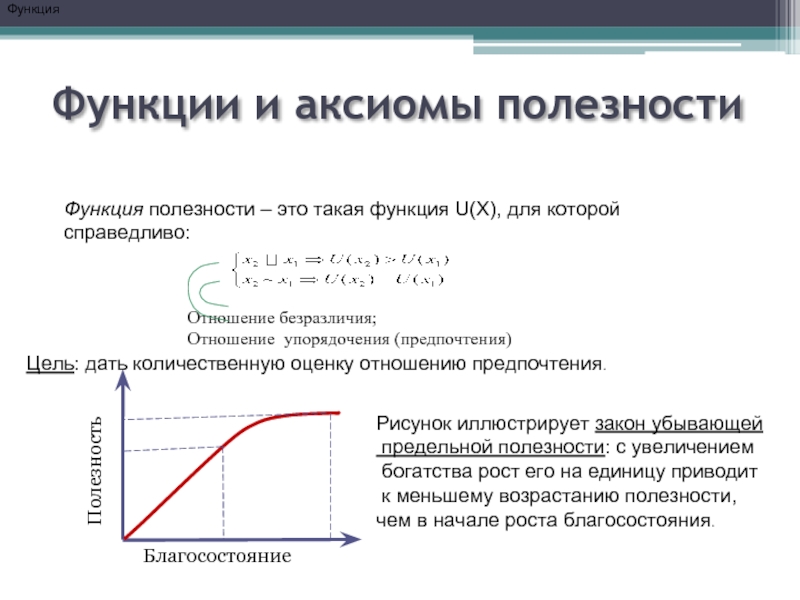
Функция полезности – это такая функция U(X),
Цель: дать количественную оценку отношению предпочтения.
Рисунок иллюстрирует закон убывающей
предельной полезности: с увеличением
богатства рост его на единицу приводит
к меньшему возрастанию полезности,
чем в начале роста благосостояния.
Полезность
Благосостояние
Слайд 6Альтернативы риска
Совершенная функция полезности – это такая функция U(x), для которой
U (x1) > U (x2) тогда и только тогда, когда
Ожидаемая полезность. Пусть определено множество X, элементы которого могут представлять собой альтернативы выбора либо последствия решений, содержащих элемент риска. Пусть на множестве Х определены два распределения вероятностей P и Q (их называют ставками, лотереями, альтернативами риска, смешанными стратегиями), для которых справедливо:
Слайд 7Линейная комбинация альтернатив
Линейной комбинацией альтернатив P и Q называется распределение R
Слайд 9Аксиомы функции полезности
Ниже полагаем:
Отношение P нерефлексивно (антирефлексивно),
т.е. справедливо:
Если
, то
Слайд 10САМОСТОЯТЕЛЬНО
Построить график вспомогательной функции V применительно к личности, которая до определенного
Создать распределение R, являющееся линейной комбинацией P и Q, где:
P: p(0$)=0,2; p(15$)=0,5; p(25$)=0,2; p(50$)=0,1.
Q: q(10$)=0,3; q(30$)=0,4;q(70$)=0,3.
α = 0,45.
Слайд 11Принятие наиболее полезных решений
Содержательная постановка задачи:
Требуется на множестве альтернатив
Слайд 12Обозначения
R – величина ресурса;
– величина
– вероятность i-го выигрыша;
затраты ресурса на выбор i-й альтернативы;
булева переменная, равная единице при
выборе i-й альтернативы и равная нулю в противном случае;
полезность i-й альтернативы.
Слайд 14Преобразование системы (1)
Пусть
Легко убедиться, что (2) представляет собой задачу о ранце.
Слайд 15ПРИМЕР 1
Уложить в рюкзак наиболее полезные в походе предметы, если
Табл. 1.
Слайд 18Решить самостоятельно
Выбрать наиболее полезные направления развития промышленности, если объем имеющихся для
Табл. 2.
Слайд 19Многофакторная полезность
Часто полезность является функцией не одного, а нескольких факторов, поэтому
Слайд 20Аддитивная многофакторная функция полезности
Функция U является аддитивной на множестве X,
Слайд 21Эквивалентные векторы
Векторы (x1, x2, ..., xm) и (y1, y2, ..., ym)
Если (x1, x2, ..., xm) ∼ (y1, y2, ..., ym) и U(X) – аддитивная функция полезности на X, то невозможно выполнение условия:
Слайд 22Многофакторная полезность
Дать формальное описание задачи и решить ее графически: девушке предлагают
первая из которых определяет полезность времени, проведенного им на работе, а вторая – дома. Сумма времен не превышает 18 часов. Кого следует выбрать девушке, если функции имеют вид:
Слайд 23Максимальная полезность i-го объекта
Формальная постановка задачи:
Следует решить три задачи, определив полезность
того, у которого этот параметр максимален.
Слайд 25Решить самостоятельно
На множестве из трех направлений развития корпорации выбрать наиболее и
Pj – вероятность получения прибыли при выборе j-го направления развития.
Nj – вероятная прибыль от j-го направления развития при условии вложения в это направление Rj средств корпорации.
Rj – средства корпорации, которые по мнению экспертов следует вложить в j-е направление, чтобы получить прибыль Nj.