- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы математической логики. Логические функции Excel. (Лекция 6) презентация
Содержание
- 1. Элементы математической логики. Логические функции Excel. (Лекция 6)
- 2. Логика - это наука, изучающая правильность суждений,
- 3. IV век Аристотель XVIII век Эйлер XVII
- 4. Логика высказываний высказывание – любое повествовательное предложение,
- 5. высказывательные формы (предикаты) – предложения, содержащие переменную.
- 6. «У кошки 4 ноги»; «Сумма углов треугольника
- 7. Простые и сложные высказывания Высказывание имеет вид
- 8. Логические операции над высказываниями Высказывание «А и
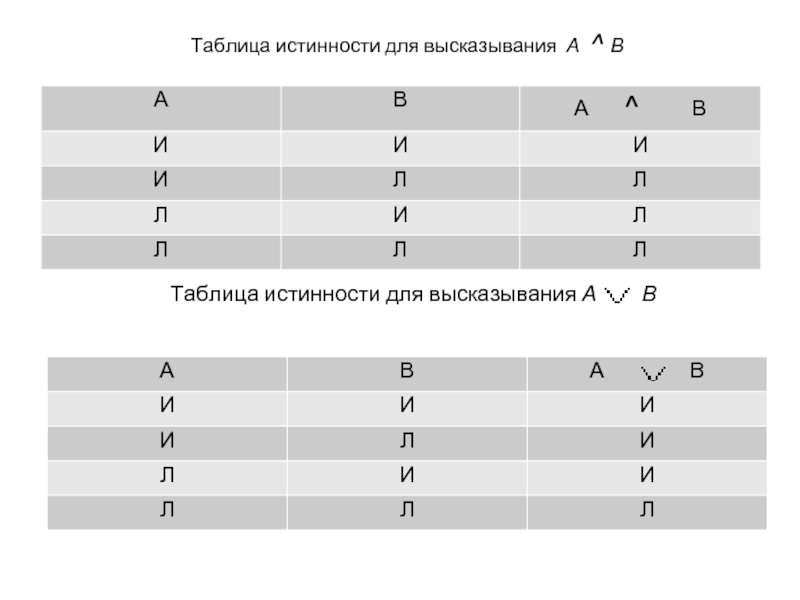
- 9. Таблица истинности для высказывания А ^ В
- 10. Отрицание Логическая операция, соответствующая логической связке
- 11. Импликация и эквиваленция Импликацией высказываний А и В
- 12. Эквиваленцией высказываний А и В называют высказывание
- 13. Язык и формулы логики высказываний Раздел математической
- 14. Определим алфавит, то есть, набор символов, которые употребляются
- 15. Определение формулы логики высказываний: Всякая логическая
- 16. Алгоритм формализации высказываний. Если высказывание – простое,
- 17. Пример Формализовать высказывание: «Неверно, что число
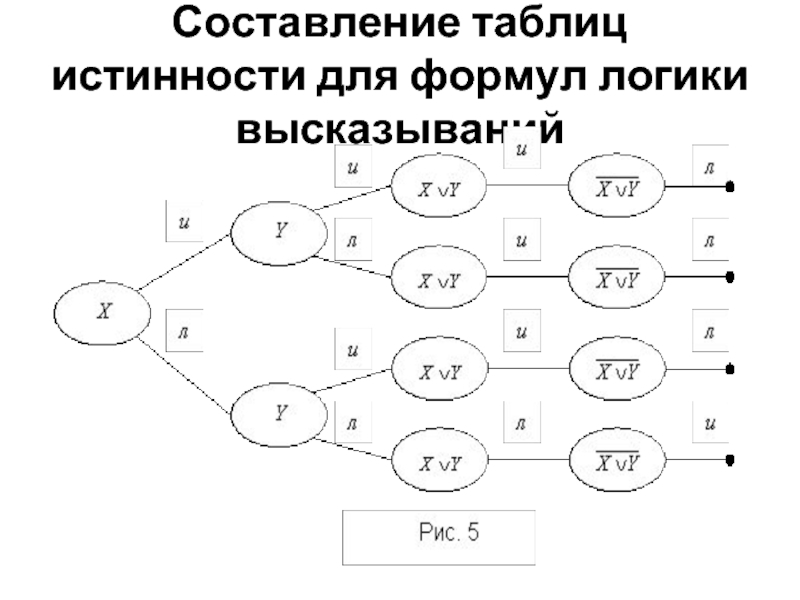
- 18. Составление таблиц истинности для формул логики высказываний
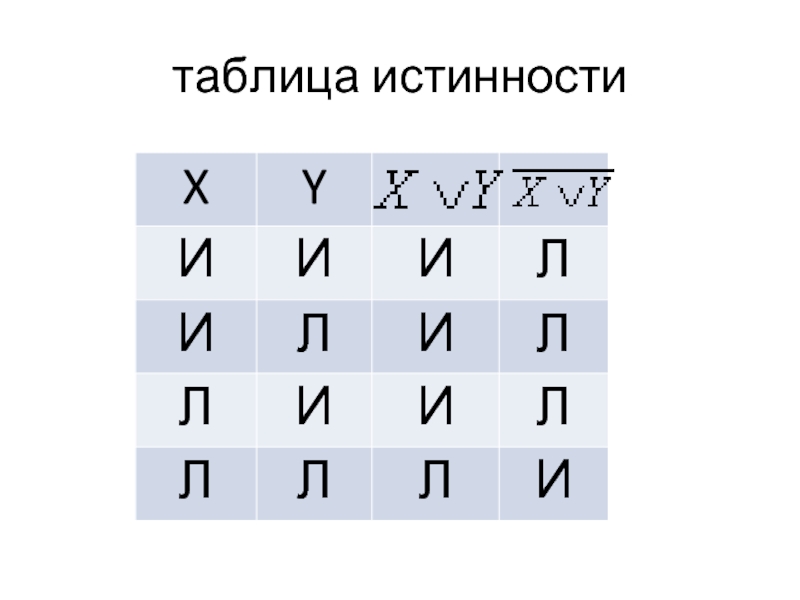
- 19. таблица истинности
- 20. Логические функции Excel Логическая функция
- 21. Логическая функция И имеет вид: - И(x1;
- 22. Логическая функция НЕ имеет вид - НЕ(x),
- 23. Логическая функция ИЛИ имеет вид:
Слайд 2Логика - это наука, изучающая правильность суждений, рассуждений и доказательств.
Суждение
Суждение ложно, если оно противоречит истинному положению вещей. Примеры ложных утверждений - «2´2 = 5», «снег - черный», «Земля плоская».
Математическая логика - это дисциплина, изучающая технику математических доказательств.
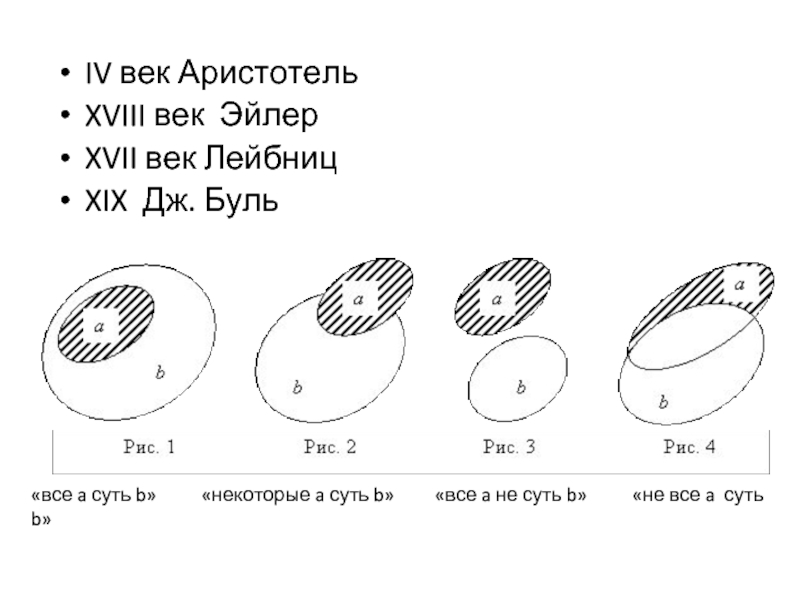
Слайд 3IV век Аристотель
XVIII век Эйлер
XVII век Лейбниц
XIX Дж. Буль
«все a суть b»
Слайд 4Логика высказываний
высказывание – любое повествовательное предложение, про которое известно, является оно
а)«сумма чисел 2 и 5 равна 7» (истинное высказывание),
б) «2 + 5 = 7» — предыдущее высказывание, записанное с помощью математических символов,
в) «для всех значений x верно
неравенство (ложное высказывание),
г) «завтра будет солнечный день» (может быть истинным или ложным).
Высказывания обозначаются заглавными буквами латинского алфавита – A, B и т.д.
Слайд 5высказывательные формы (предикаты) – предложения, содержащие переменную. Например, выражение «
Слайд 6«У кошки 4 ноги»;
«Сумма углов треугольника равна 180°»;
«Температура кипения воды 180°»;
«У
«2x = 3y»;
«Число 5 делится на 2 без остатка»;
«x < 5»;
«У квадрата есть только один прямой угол»;
«a + b = 10»;
«Дважды два – четыре»;
«Пустое множество не имеет подмножеств».
Слайд 7Простые и сложные высказывания
Высказывание имеет вид повествовательного предложения. Из двух таких предложений можно
Предложения, не являющиеся составными, называются элементарными.
Соответственно, если можно судить об истинности или ложности таких предложений, то они будут называться простыми и составными высказываниями.
Слайд 8Логические операции над высказываниями
Высказывание «А и В», истинное, если истинны оба
Высказывание «А или В», истинное, если истинно хотя бы одно из высказываний А или В, и ложное лишь в одном случае, когда оба высказывания А и В ложны, называется дизъюнкцией этих высказываний и обозначается А В.
Слайд 10 Отрицание
Логическая операция, соответствующая логической связке «не», называется отрицанием.
Высказывание «не А»,
Слайд 11Импликация и эквиваленция
Импликацией высказываний А и В называют высказывание
Слайд 12Эквиваленцией высказываний А и В называют высказывание
Слайд 13Язык и формулы логики высказываний
Раздел математической логики, в котором изучают свойства выражений,
Пусть X, Y, Z– переменные, обозначающие элементарные логические высказывания или их значения истинности. Такие переменные будем называть логическими переменными.
С помощью логических переменных и символов логических операций можно формализовать любое логическое высказывание. Таким образом, логическое высказывание заменяется формулой, отражающей логическую структуру этого высказывания.
Например, высказывание «Число а делится на 6 тогда и только тогда, когда а делится на 2, и а делится на 3» формализуется в виде .
Слайд 14Определим алфавит, то есть, набор символов, которые употребляются в логике высказываний:
1.
2. И, Л – символы, обозначающие логические константы «истина», «ложь»,
3. - символы логических операций,
4. ( , ) – скобки, вспомогательные символы, служащие для указания порядка выполнения логических операций.
Слайд 15Определение формулы логики высказываний:
Всякая логическая переменная есть формула.
2. Символы И, Л есть
3. Если есть формула, то есть формула.
4. Если есть формулы, то , ,
, есть формулы.
5. Никаких других формул в логике высказываний нет.
Слайд 16Алгоритм формализации высказываний.
Если высказывание – простое, то ему ставится в соответствие элементарная формула.
Если высказывание – составное, то для составления формулы требуется:
а) выделить все элементарные высказывания и логические связки, образующие данное высказывание,
в) заменить их соответствующими символами,
с) расставить скобки в соответствии со смыслом данного высказывания.
Слайд 17Пример
Формализовать высказывание: «Неверно, что число 500 делится на 3 или на 13»
Пусть
Y – «число 500 делится на 13».
Тогда данное сложное высказывание имеет вид
Слайд 20Логические функции Excel
Логическая функция ЕСЛИ имеет вид:
ЕСЛИ(x1; x2; x3),
где x1, x2, x3 – аргументы
x1 - логическое выражение,
x2, x3 – любые выражения, разрешенные в Excel;
причем вычисляется x2, если x1 имеет значение ИСТИНА, и x3, если x1 имеет значение ЛОЖЬ.
Если третий аргумент функции не определен, то ошибки в записи функции нет – в этом случае ей присваивается значение ЛОЖЬ, если условие не выполнено. Если ничего не нужно вычислять при невыполнении условия, следует в качестве третьего аргумента задать пробел как текст.
Примеры: ЕСЛИ(A5>0;LN(A5);-1);
ЕСЛИ(B2<>0;1/B2;” ”)
Слайд 21Логическая функция И имеет вид: - И(x1; x2;; …;xn), где x1;
Функция может содержать до 30 аргументов.
Функция И принимает значение ИСТИНА, если все ее аргументы истинны, в противном случае она принимает значение ЛОЖЬ.
Функция может применяться для задания сложного условия, определяемого системой равенств и неравенств:
или, в форме логических высказываний,
где xi – равенство или неравенство, которое может быть истинным или ложным.
Слайд 22Логическая функция НЕ имеет вид - НЕ(x), где x – логическое
Слайд 23Логическая функция ИЛИ имеет вид:
ИЛИ(x1; x2, …;xn),
где x1;
Функция может содержать до 30 аргументов.
Функция ИЛИ принимает значение ИСТИНА, если хотя бы один из ее аргументов есть ИСТИНА, в противном случае она принимает значение ЛОЖЬ.
Функция применяется для задания сложного условия определяемого совокупностью неравенств
или
где xi – равенство или неравенство, которое может быть истинным или ложным.